WikiDer > Постулат АА
эта статья в значительной степени или полностью полагается на один источник. (Ноябрь 2010 г.) |
В Евклидова геометрия, то Постулат АА заявляет, что два треугольники подобны, если им соответствуют два углы конгруэнтный.
Постулат АА следует из того факта, что сумма внутренние углы из треугольник всегда равен 180 °. Зная два угла, например 32 ° и 64 °, мы знаем, что следующий угол равен 84 °, потому что 180- (32 + 64) = 84. (Иногда это называют постулатом ААА, который верен во всех отношениях, но двух углов вполне достаточно.)
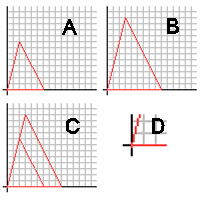
Постулат можно лучше понять, если действовать в обратном порядке. Два треугольника на сетках A и B - это аналогичный, на 1,5 расширение от A до B. Если они выровнены, как в сетке C, очевидно, что угол в исходной точке совпадает с другим углом (D). Мы также знаем, что пара сторон, противоположных началу координат, параллельна. Мы знаем это, потому что пары сторон вокруг них похожи, исходят из одной точки и выстраиваются друг с другом. Затем мы можем посмотреть на стороны вокруг параллелей как трансверсали, а значит, и соответствующие углы совпадают. Используя это рассуждение, мы можем сказать, что подобные треугольники имеют равные углы.
Рекомендации
- http://hanlonmath.com/pdfFiles/464Chapter7Sim.Poly.pdf (Неиспользуемый источник)