WikiDer > Формула Бете
Эта статья возможно содержит оригинальные исследования. (Октябрь 2020) (Узнайте, как и когда удалить этот шаблон сообщения) |
В Формула Бете описывает[1] средняя потеря энергии на пройденное расстояние быстрых заряженные частицы (протоны, альфа-частицы, атомный ионы) проходящего материала (или, альтернативно, останавливающая сила материала). Для электронов потери энергии немного отличаются из-за их малой массы (требующей релятивистских поправок) и их неразличимость, и поскольку они несут гораздо большие потери Тормозное излучение, необходимо добавить условия, чтобы учесть это. Быстрые заряженные частицы, движущиеся через вещество, взаимодействуют с электронами атомов в веществе. Взаимодействие возбуждает или ионизирует атомы, что приводит к потере энергии движущейся частицы.
В нерелятивистский версия была найдена Ганс Бете в 1930 г .; релятивистская версия (показанная ниже) была найдена им в 1932 году.[2] Наиболее вероятная потеря энергии отличается от средней потери энергии и описывается распределением Ландау-Вавилова.[3]
Формулу Бете иногда называют «формулой Бете-Блоха», но это вводит в заблуждение (см. Ниже).
Формула
Для частицы со скоростью v, обвинять z (кратные заряду электрона), а энергия E, путешествуя на расстояние Икс в цель электрон числовая плотность п и средний потенциал возбуждения я, релятивистская версия формулы в единицах СИ:[2]
(1)
куда c это скорость света и ε0 то диэлектрическая проницаемость вакуума, , е и ме то заряд электрона и масса покоя соответственно.
Здесь электронную плотность материала можно рассчитать по формуле
куда ρ плотность материала, Z это атомный номер, А это относительная атомная масса, NА то Число Авогадро и Mты то Постоянная молярной массы.
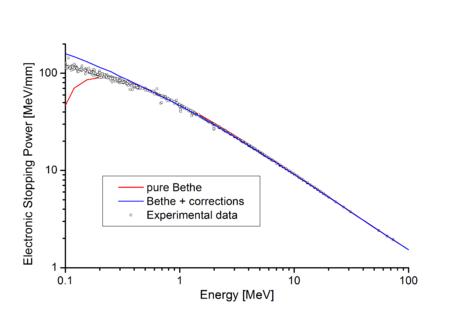
На рисунке справа маленькие кружки - экспериментальные результаты, полученные из измерений различных авторов, а красная кривая - формула Бете.[4] Очевидно, теория Бете очень хорошо согласуется с экспериментом при высоких энергиях. Согласие даже лучше, когда применяются поправки (см. Ниже).
При малых энергиях, т.е. при малых скоростях частицы β << 1 формула Бете сводится к
(2)
В этом можно убедиться, предварительно заменив βc к v в экв. (1) а затем пренебрегая β2 из-за небольшого размера.
Таким образом, при низкой энергии потери энергии по формуле Бете уменьшается примерно как v−2 с увеличением энергии. Он достигает минимума примерно за E = 3Mc2, куда M - масса частицы (для протонов это будет около 3000 МэВ). Для очень релятивистский случаи β ≈ 1, потери энергии снова увеличиваются логарифмически из-за поперечной составляющей электрического поля.
Средний потенциал возбуждения

В теории Бете материал полностью описывается одним числом - средний потенциал возбуждения я. В 1933 г. Феликс Блох показали, что средний потенциал ионизации атомов приблизительно определяется выражением
(3)
куда Z атомный номер атомов материала. Если это приближение ввести в формулу (1) выше, получается выражение, которое часто называют Формула Бете-Блоха. Но поскольку теперь у нас есть точные таблицы я как функция Z (см. ниже), использование такой таблицы даст лучшие результаты, чем использование формулы (3).
На рисунке приведены нормированные значения я, взятый из таблицы.[5] Пики и спады на этом рисунке приводят к соответствующим впадинам и пикам тормозной способности. Они называются "Z2-колебания "или"Z2-структура »(где Z2 = Z означает атомный номер мишени).
Поправки к формуле Бете
Формула Бете действительна только для достаточно высоких энергий, чтобы заряженная атомная частица ( ион) не несет с собой никаких атомных электронов. При меньших энергиях, когда ион несет электроны, это эффективно снижает его заряд, и, таким образом, снижается тормозная способность. Но даже если атом полностью ионизирован, поправки необходимы.
Бете нашел свою формулу, используя квантово-механический теория возмущений. Следовательно, его результат пропорционален квадрату заряда z частицы. Описание можно улучшить, если учесть поправки, соответствующие более высоким степеням z. Эти Эффект Баркаса-Андерсена (пропорционально z3, после Уолтер Х. Баркас и Ганс Хенрик Андерсен), а Блох-коррекция (пропорционально z4). Кроме того, необходимо учитывать, что атомные электроны пройденного материала не являются стационарными ("исправление оболочки").
Упомянутые поправки были встроены, например, в программы PSTAR и ASTAR, с помощью которых можно рассчитать тормозную способность для протонов и альфа-частиц.[6] Поправки велики при низкой энергии и становятся все меньше и меньше по мере увеличения энергии.
При очень высоких энергиях Фермипоправка на плотность[5] нужно также добавить.
Проблема номенклатуры
При описании программ PSTAR и ASTAR Национальный институт стандартов и технологий[6] вызывает формулу (1) "Формула останавливающей силы Бете".
С другой стороны, в Обзоре физики элементарных частиц за 2008 г.[7] формула получила название «уравнение Бете-Блоха», хотя выражение Блоха (3) не фигурировал в формуле. Но в более поздних изданиях формула теперь называется «формулой Бете».[8][9]Предположительно, «Блох» в «Бете-Блохе» означал блоховскую поправку (см. Выше). Но тогда более логичным показалось бы обозначение «Бете-Баркас-Блох».
Смотрите также
Рекомендации
- ^ Х. Бете и Дж. Ашкин в "Экспериментальной ядерной физике", изд. Э. Сегре, Дж. Вили, Нью-Йорк, 1953, стр. 253.
- ^ а б Зигмунд, Питер Проникновение частиц и радиационные эффекты. Серия Спрингера в науках о твердом теле, 151. Берлин Гейдельберг: Springer-Verlag. ISBN 3-540-31713-9 (2006)
- ^ Бихзель, Ганс (1988-07-01). «Забегание в тонких кремниевых детекторах». Обзоры современной физики. Американское физическое общество (APS). 60 (3): 663–699. Дои:10.1103 / revmodphys.60.663. ISSN 0034-6861.
- ^ «Тормозящая сила для легких и более тяжелых ионов». 2015-04-15. Получено 2015-11-01.
- ^ а б Отчет 49 Международной комиссии по радиационным единицам и измерениям, «Тормозящие способности и диапазоны для протонов и альфа-частиц», Бетесда, Мэриленд, США (1993)
- ^ а б NISTИК 4999, Таблицы тормозной способности и диапазона
- ^ Amsler, C .; Дозер, М .; Антонелли, М .; Asner, D.M .; Babu, K.S .; и другие. (Группа данных по частицам) (2008). «Обзор физики элементарных частиц» (PDF). Письма по физике B. Elsevier BV. 667 (1–5): 1–6. Дои:10.1016 / j.physletb.2008.07.018. ISSN 0370-2693.
- ^ Накамура, К; и другие. (Группа данных по частицам) (01.07.2010). «Обзор физики элементарных частиц». Журнал физики G: Ядерная физика и физика элементарных частиц. IOP Publishing. 37 (7A): 075021. Дои:10.1088 / 0954-3899 / 37 / 7a / 075021. ISSN 0954-3899.
- ^ Beringer, J .; Arguin, J. -F .; Barnett, R.M .; Copic, K .; Dahl, O .; и другие. (Группа данных по частицам) (2012-07-20). «Обзор физики элементарных частиц». Физический обзор D. Американское физическое общество (APS). 86 (1): 0100001. Дои:10.1103 / Physrevd.86.010001. ISSN 1550-7998.
внешняя ссылка
- Функция Straggling. Распределение потерь энергии заряженных частиц
- Оригинальная публикация: Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie in "Annalen der Physik", Vol. 397 (1930) 325 -400
- Прохождение заряженных частиц через вещество, с графиком
- Тормозная способность протонов и альфа-частиц
- Графики и данные останавливающей мощности
![-leftlangle {frac {dE} {dx}} ightangle = {frac {4pi} {m_ {e} c ^ {2}}} cdot {frac {nz ^ {2}} {eta ^ {2}}} cdot left ({frac {e ^ {2}} {4pi varepsilon _ {0}}} ight) ^ {2} cdot left [ln left ({frac {2m_ {e} c ^ {2} eta ^ {2}} { Icdot (1-эта ^ {2})}} ight) - эта ^ {2} ight]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dd473093a5b5e89894bd589a0a2f58c669ed1b7)


![- {frac {dE} {dx}} = {frac {4pi nz ^ {2}} {m_ {e} v ^ {2}}} cdot left ({frac {e ^ {2}} {4pi varepsilon _ { 0}}} ight) ^ {2} cdot left [ln left ({frac {2m_ {e} v ^ {2}} {I}} ight) ight].](https://wikimedia.org/api/rest_v1/media/math/render/svg/49ffd089c1ec85c3cafa26ad6104042d0151eb94)
