WikiDer > Теорема Биркгофа о представлении - Википедия

Речь идет о теория решетки. Для других результатов с похожими названиями см. Теорема Биркгофа (значения).

В математика, Теорема Биркгофа о представлении для распределительных решеток утверждает, что элементы любых конечный распределительная решетка можно представить как конечные множества, таким образом, что операции решетки соответствуют союзы и перекрестки наборов. Теорема может быть интерпретирована как предоставление индивидуальная переписка между распределительными решетками и частичные заказы, между квазиординальные пространства знаний и предварительные заказы, или между конечные топологические пространства и предварительные заказы. Он назван в честь Гаррет Биркгоф, который опубликовал доказательство этого в 1937 году.^[1]

Название «теорема Биркгофа о представлении» также применялось к двум другим результатам Биркгофа, одному из которых 1935 г. представление булевых алгебр как семейства множеств, замкнутых относительно объединения, пересечения и дополнения (так называемые поля наборов, тесно связанный с кольца наборов используется Биркгофом для представления распределительных решеток), и Теорема Биркгофа о HSP представление алгебр как произведения неприводимых алгебр. Теорема Биркгофа о представлении также получила название основная теорема для конечных дистрибутивных решеток.^[2]

Понимание теоремы

Многие решетки могут быть определены таким образом, что элементы решетки представлены множествами, операция соединения решетки представлена ​​объединением множеств, а операция встречи решетки представлена ​​пересечением множеств. Например, Логическая решетка определенная из семейства всех подмножеств конечного множества, обладает этим свойством. В целом любой конечное топологическое пространство имеет решетку множеств как семейство открытых множеств. Поскольку множества союзов и пересечений подчиняются распределительный закон, любая определенная таким образом решетка является дистрибутивной решеткой. Теорема Биркгофа утверждает, что на самом деле все конечные дистрибутивные решетки могут быть получены таким образом, и более поздние обобщения теоремы Биркгофа утверждают то же самое для бесконечных дистрибутивных решеток.

Примеры

Дистрибутивная решетка делителей 120 и ее представление в виде множеств степеней простых чисел.

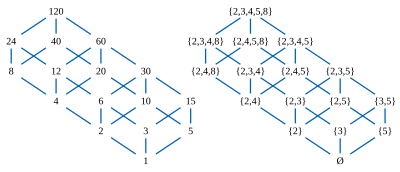
Рассмотрим делители некоторого составного числа, такого как (на рисунке) 120, частично упорядоченного по делимости. Любые два делителя 120, такие как 12 и 20, имеют уникальный наибольший общий делитель 12 ∧ 20 = 4, наибольшее число, которое делит их обоих, и уникальное наименьший общий множитель 12 ∨ 20 = 60; оба эти числа также являются делителями 120. Эти две операции ∨ и ∧ удовлетворяют распределительный закон, в любой из двух эквивалентных форм: (Икс ∧ у) ∨ z = (Икс ∨ z) ∧ (у ∨ z) и (Икс ∨ у) ∧ z = (Икс ∧ z) ∨ (у ∧ z), для всех Икс, у, и z. Следовательно, дивизоры образуют конечную распределительная решетка.

Каждому дивизору можно сопоставить множество основные силы которые делят его: таким образом, 12 связано с набором {2,3,4}, а 20 связано с набором {2,4,5}. Тогда 12 ∧ 20 = 4 ассоциируется с набором {2,3,4} ∩ {2,4,5} = {2,4}, а 12 ∨ 20 = 60 ассоциируется с множеством {2,3,4 } ∪ {2,4,5} = {2,3,4,5}, поэтому операции соединения и пересечения решетки соответствуют объединению и пересечению множеств.

Степени простых чисел 2, 3, 4, 5 и 8, появляющиеся как элементы в этих наборах, могут сами быть частично упорядочены по делимости; в этом меньшем частичном порядке 2 ≤ 4 ≤ 8, и между другими парами нет отношений порядка. 16 наборов, которые связаны с делителями 120, являются нижние наборы этого меньшего частичного порядка подмножества элементов такие, что если Икс ≤ у и у принадлежит подмножеству, то Икс также должен принадлежать к подмножеству. Из любого нижнего набора L, можно восстановить связанный делитель, вычислив наименьшее общее кратное степеней простых чисел в L. Таким образом, частичный порядок пяти степеней простого числа 2, 3, 4, 5 и 8 несет достаточно информации для восстановления всей исходной решетки делимости на 16 элементов.

Теорема Биркгофа утверждает, что эта связь между операциями и решетки делителей и операциями ∩ и ассоциированных множеств степеней простых чисел не случайна и не зависит от конкретных свойств простых чисел и делимости: элементов любая конечная дистрибутивная решетка может быть таким же образом связана с нижними множествами частичного порядка.

В качестве другого примера, применение теоремы Биркгофа к семейству подмножества из п-элементный набор, частично упорядоченный включением, производит свободная распределительная решетка с п генераторы. Количество элементов в этой решетке определяется выражением Числа Дедекинда.

Частичный порядок неприводимых к соединению

В решетке элемент Икс является неприводимый к соединению если Икс не является соединением конечного набора других элементов. Эквивалентно, Икс является неприводимым к соединению, если он не является ни нижним элементом решетки (соединением нулевых элементов), ни соединением любых двух меньших элементов. Например, в решетке делителей числа 120 нет пары элементов, объединение которых равно 4, поэтому 4 неприводима по объединению. Элемент Икс является присоединиться к первому если, когда Икс ≤ у ∨ z, либо Икс ≤ у или же Икс ≤ z. В той же решетке 4 простое число: всякий раз, когда lcm (у,z) делится на 4, хотя бы одно из у и z сам должен делиться на 4.

В любой решетке элемент с простым объединением должен быть неприводимым по объединению. Эквивалентно, элемент, который не является неприводимым к соединению, не является простым соединением. Ведь если элемент Икс не является неприводимым к соединению, существуют меньшие у и z такой, что Икс = у ∨ z. Но потом Икс ≤ у ∨ z, и Икс не меньше или равно либо у или же z, показывая, что это не простое соединение.

Существуют решетки, в которых первичные элементы соединения образуют собственное подмножество неприводимых элементов соединения, но в дистрибутивной решетке эти два типа элементов совпадают. Ибо предположим, что Икс неприводимо к соединению, и что Икс ≤ у ∨ z. Это неравенство эквивалентно утверждению, что Икс = Икс ∧ (у ∨ z), и по закону распределения Икс = (Икс ∧ у) ∨ (Икс ∧ z). Но с тех пор Икс неприводимо к соединению, по крайней мере один из двух членов в этом соединении должен быть Икс сам, показывая, что либо Икс = Икс ∧ у (эквивалентно Икс ≤ у) или же Икс = Икс ∧ z (эквивалентно Икс ≤ z).

Решёточный порядок на подмножестве неразложимых по соединению элементов образует частичный заказ; Теорема Биркгофа утверждает, что сама решетка может быть восстановлена ​​из нижних множеств этого частичного порядка.

Теорема Биркгофа

Дистрибутивная примерная решетка с неприводимыми к объединению элементами a, ..., g (затененные узлы). Нижнее множество, которому соответствует узел по изоморфизму Биркгофа, показано синим цветом.

В любом частичном порядке нижние наборы образуют решетку, в которой частичный порядок решетки задается включением множества, операция соединения соответствует объединению множеств, а операция встречи соответствует пересечению множеств, поскольку объединения и пересечения сохраняют свойство быть нижним множеством. Поскольку объединения и пересечения множеств подчиняются закону распределения, это распределительная решетка. Теорема Биркгофа утверждает, что любая конечная дистрибутивная решетка может быть построена таким образом.

Теорема. Любая конечная дистрибутивная решетка L изоморфна решетке нижних множеств частичного порядка объединяемых неприводимых элементов L.

То есть существует взаимно однозначное соответствие между элементами L и нижние множества частичного порядка. Нижний набор, соответствующий элементу Икс из L представляет собой просто набор неприводимых к соединению элементов L которые меньше или равны Икс, а элемент L соответствующий нижнему набору S неприводимых к объединению элементов является объединением S.

Для любого нижнего набора S соединяемых неприводимых элементов, пусть Икс быть объединением S, и разреши Т - нижний набор неприводимых к соединению элементов, меньший или равный Икс. потом S = Т. Ведь каждый элемент S явно принадлежит Т, и любой неприводимый к соединению элемент, меньший или равный Икс должен (по принципу простоты соединения) быть меньше или равным одному из членов S, и поэтому должен (в предположении, что S нижнее множество) принадлежат S сам. И наоборот, для любого элемента Икс из L, позволять S - неприводимые к соединению элементы, меньшие или равные Икс, и разреши у быть объединением S. потом Икс = у. Поскольку, как соединение элементов, меньших или равных Икс, у не может быть больше, чем Икс сам, но если Икс неприводимо к соединениям, то Икс принадлежит S а если Икс является объединением двух или более неразложимых элементов, то они снова должны принадлежать S, так у ≥ Икс. Следовательно, соответствие взаимно однозначно и теорема доказана.

Кольца наборов и предзаказов

Биркгоф (1937) определил кольцо множеств быть семейство наборов то есть закрыто при операциях объединения множеств и пересечений множеств; позже, мотивированные приложениями в математическая психология, Дуаньон и Фальмань (1999) назвал ту же структуру квазиординал пространство знаний. Если множества в кольце множеств упорядочены по включению, они образуют дистрибутивную решетку. Элементам наборов можно дать Предварительный заказ в котором Икс ≤ у всякий раз, когда какой-либо набор в кольце содержит Икс но нет у. Само кольцо множеств тогда является семейством нижних множеств этого предпорядка, и любой предпорядок таким образом порождает кольцо множеств.

Функциональность

Теорема Биркгофа, как указано выше, является соответствием между отдельными частичными порядками и дистрибутивными решетками. Однако его также можно распространить на соответствие между сохраняющими порядок функциями частичных порядков и ограниченные гомоморфизмы соответствующих дистрибутивных решеток. В этом соответствии направление этих карт меняется на противоположное.

Позволять 2 обозначим частичный порядок на двухэлементном множестве {0, 1} с отношением порядка 0 <1, и (следуя Стэнли) пусть J (P) обозначим дистрибутивную решетку нижних множеств конечного частичного порядка п. Тогда элементы J (P) однозначно соответствуют сохраняющим порядок функциям из п к 2.^[2] Ведь если ƒ - такая функция, то ƒ⁻¹(0) образует нижнее множество, и наоборот, если L является нижним множеством, можно определить сохраняющую порядок функцию ƒ_L что отображает L в 0, и это отображает остальные элементы п к 1. Если грамм - любая функция сохранения порядка из Q к п, можно определить функцию грамм* из J (P) к J (Q) который использует состав функций отобразить любой элемент L из J (P) к ƒ_L ∘ грамм. Эта составная функция отображает Q к 2 и поэтому соответствует элементу грамм*(L) = (ƒ_L ∘ грамм)⁻¹(0) из J (Q). Далее при любом Икс и у в J (P), грамм*(Икс ∧ у) = грамм*(Икс) ∧ грамм*(у) (элемент Q отображается грамм в нижний набор Икс ∩ у тогда и только тогда, когда оба принадлежат к набору элементов, отображаемых в Икс и набор элементов, сопоставленных с у) и симметрично грамм*(Икс ∨ у) = грамм*(Икс) ∨ грамм*(у). Кроме того, нижний элемент J (P) (функция, отображающая все элементы п в 0) отображается грамм* к нижнему элементу J (Q), а верхний элемент J (P) отображается грамм* в верхний элемент J (Q). То есть, грамм* - гомоморфизм ограниченных решеток.

Однако элементы п сами соответствуют однозначно с ограниченными решеточными гомоморфизмами из J (P) к 2. Ведь если Икс любой элемент п, можно определить ограниченный решеточный гомоморфизм j_Икс который отображает все нижние множества, содержащие Икс в 1, а все остальные нижние множества в 0. И для любого решеточного гомоморфизма из J (P) к 2, элементы J (P) которые отображаются в 1, должны иметь уникальный минимальный элемент Икс (пересечение всех элементов, отображенных в 1), которое должно быть неприводимым к соединению (оно не может быть объединением любого набора элементов, отображенных в 0), поэтому каждый решеточный гомоморфизм имеет вид j_Икс для некоторых Икс. Опять же, из любого ограниченного решеточного гомоморфизма час из J (P) к J (Q) можно использовать композицию функций, чтобы определить сохраняющую порядок карту час* из Q к п. Можно проверить, что грамм** = грамм для любой сохраняющей порядок карты грамм из Q к п и это и час** = час для любого ограниченного решеточного гомоморфизма час из J (P) к J (Q).

В теоретико-категорийный терминология, J это контравариантный гом-функтор J = Hom (-,2), определяющий двойственность категорий между, с одной стороны, категорией конечных частичных порядков и сохраняющих порядок отображений, а с другой стороны, категорией конечных дистрибутивных решеток и ограниченных решеточных гомоморфизмов.

Обобщения

Бесконечные распределительные решетки

В бесконечной дистрибутивной решетке может и не быть случай, когда нижние множества неприводимых к объединению элементов находятся во взаимно однозначном соответствии с элементами решетки. В самом деле, не может быть вообще никаких соединений-неприводимых. Это происходит, например, в решетке всех натуральных чисел, упорядоченных в порядке, обратном обычному порядку делимости (так Икс ≤ у когда у разделяет Икс): любой номер Икс можно выразить как объединение чисел xp и xq куда п и q отличны простые числа. Однако элементы в бесконечных дистрибутивных решетках все еще могут быть представлены в виде множеств через Теорема Стоуна о представлении для распределительных решеток вид Каменная двойственность в котором каждому элементу решетки соответствует компактный открытый набор в определенном топологическое пространство. Эту обобщенную теорему о представлении можно выразить как теоретико-категориальный двойственность между распределительными решетками и спектральные пространства (иногда называемые когерентными пространствами, но не то же самое, что когерентные пространства в линейной логике), топологические пространства, в которых открытые компакты замкнуты относительно пересечения и образуют основание для топологии.^[3] Хилари Пристли показал, что теорема Стоуна о представлении может быть интерпретирована как расширение идеи представления элементов решетки нижними множествами частичного порядка с использованием идеи Нахбина об упорядоченных топологических пространствах. Каменные пространства с дополнительным частичным порядком, связанные с топологией через Аксиома разделения Пристли может также использоваться для представления ограниченных дистрибутивных решеток. Такие пространства известны как Пространства Пристли. Далее, некоторые битопологические пространства, а именно попарные каменные пространства, обобщить оригинальный подход Стоуна, используя два топологии на множестве для представления абстрактной распределительной решетки. Таким образом, теорема Биркгофа о представлении распространяется на случай бесконечных (ограниченных) дистрибутивных решеток по крайней мере тремя различными способами, суммируемыми в теория двойственности для дистрибутивных решеток.

Медианные алгебры и связанные графы

Теорема Биркгофа о представлении также может быть обобщена на конечные структуры, отличные от дистрибутивных решеток. В распределительной решетке самодуальная медианная операция^[4]

${ Displaystyle м (Икс, Y, Z) = (Икс Ви Y) клин (х Ви Z) клин (у Ви Z) = (х клин у) Ви (х клин г) vee (y wedge z)}$

рождает медианная алгебра, а покрывающее отношение решетки образует медианный график. Конечные медианные алгебры и медианные графы имеют двойственную структуру как множество решений 2-выполнимость пример; Бартелеми и Константин (1993) сформулируем эту структуру эквивалентно как семейство исходных стабильные наборы в смешанный график.^[5] Для дистрибутивной решетки соответствующий смешанный граф не имеет неориентированных ребер, а исходные стабильные множества - это просто нижние множества переходное закрытие графа. Аналогично, для распределительной решетки граф импликации экземпляра 2-выполнимости можно разделить на два связанные компоненты, одна для положительных переменных экземпляра, а другая - для отрицательных переменных; транзитивное замыкание положительного компонента является лежащим в основе частичным порядком дистрибутивной решетки.

Конечные дистрибутивные решетки и матроиды

Другой результат, аналогичный теореме Биркгофа о представлении, но применимый к более широкому классу решеток, - это теорема Эдельман (1980) что любая конечная дистрибутивная решетка может быть представлена ​​как антиматроид, семейство множеств, замкнутых относительно объединений, но в котором замыкание по пересечениям заменено свойством, что каждое непустое множество имеет удаляемый элемент.

Смотрите также

• Решетка стабильных соответствий, также представляющий любую конечную дистрибутивную решетку

Примечания

Рекомендации

• Barthélemy, J.P .; Константин, Дж. (1993), "Медианные графы, параллелизм и положения", Дискретная математика, 111 (1–3): 49–63, Дои:10.1016 / 0012-365X (93) 90140-O.
• Биркофф, Гарретт (1937), «Кольца множеств», Математический журнал герцога, 3 (3): 443–454, Дои:10.1215 / S0012-7094-37-00334-X.
• Биркофф, Гарретт; Поцелуй, С. А. (1947), «Тернарная операция в распределительных решетках», Бюллетень Американского математического общества, 53 (1): 749–752, Дои:10.1090 / S0002-9904-1947-08864-9, МИСТЕР 0021540.
• Doignon, J.P .; Falmagne, J.-Cl. (1999), Пространства знаний, Springer-Verlag, ISBN 3-540-64501-2.
• Эдельман, Пол Х. (1980), "Встречно-распределительные решетки и анти-обменное замыкание", Универсальная алгебра, 10 (1): 290–299, Дои:10.1007 / BF02482912.
• Джонстон, Питер (1982), «II.3 Связанные места», Каменные Пространства, Cambridge University Press, стр. 62–69, ISBN 978-0-521-33779-3.
• Пристли, Х.А. (1970), "Представление дистрибутивных решеток с помощью упорядоченных пространств Стоуна", Бюллетень Лондонского математического общества, 2 (2): 186–190, Дои:10.1112 / blms / 2.2.186.
• Пристли, Х.А. (1972), "Упорядоченные топологические пространства и представление дистрибутивных решеток", Труды Лондонского математического общества, 24 (3): 507–530, Дои:10.1112 / плмс / с3-24.3.507, HDL:10338.dmlcz / 134149.
• Стэнли, Р. П. (1997), Перечислительная комбинаторика, Том I, Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, стр. 104–112..