WikiDer > Центростремительный сплайн Катмулла – Рома - Википедия
В компьютерная графика, центростремительный шлиц Катмулла – Рома это вариантная форма Шпонка Катмулла-Рома, первоначально сформулированный Эдвин Кэтмелл и Рафаэль Ром,[1] который можно оценить с помощью рекурсивного алгоритма, предложенного Барри и Голдманом.[2] Это тип интерполирующего сплайна (кривая, проходящая через контрольные точки), определяемых четырьмя контрольными точками. , с кривой, построенной только из к .
Определение
Позволять обозначают точку. Для сегмента кривой определяется точками и последовательность узлов , центростремительный шлиц Катмулла – Рома можно получить с помощью:
куда
и
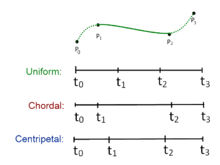
в котором варьируется от 0 до 1 для параметризации узла, и с . Для центростремительного сплайна Катмулла – Рома значение является . Когда , полученная кривая является стандартной равномерный шлиц Катмулла – Рома; когда , продукт хордовый шлиц Катмулла – Рома.
Подключение в сплайн-уравнения и показывает, что значение сплайновой кривой при является . Аналогично, подставляя в уравнения сплайна показывает, что в . Это верно независимо от значения поскольку уравнение для не требуется для расчета стоимости в точках и .
Расширение до трехмерных точек просто достигается путем рассмотрения общая 3D-точка и
Преимущества
Центростремительный сплайн Катмулла-Рома обладает несколькими желательными математическими свойствами по сравнению с исходной формулой и другими типами формулировки Катмулла-Рома.[3] Во-первых, он не будет образовывать петлю или самопересечение внутри сегмента кривой. Второй, куспид никогда не произойдет внутри сегмента кривой. В-третьих, более пристально следует за контрольными точками.[нечеткий]
Другое использование
В компьютерное зрение, центростремительный сплайн Катмулла-Рома был использован для формулировки активной модели сегментации. Метод называется активная сплайн-модель.[4] Модель разработана на основе активная модель формы, но использует центростремительный сплайн Катмулла-Рома для соединения двух последовательных точек (в активной модели формы используется простая прямая линия), поэтому общее количество точек, необходимых для изображения формы, меньше. Использование центростремительного сплайна Катмулла-Рома значительно упрощает обучение модели формы и позволяет лучше редактировать контур после сегментации.
Пример кода на Python
Ниже представлена реализация сплайна Катмалла – Рома в Python который производит график, показанный ниже.
импорт тупойимпорт matplotlib.pyplot в качестве pltdef CatmullRomSpline(P0, P1, P2, P3, nОчки=100): """ P0, P1, P2 и P3 должны быть парами точек (x, y), которые определяют сплайн Катмулла-Рома. nPoints - это количество точек, включаемых в этот сегмент кривой. """ # Преобразуйте точки в numpy, чтобы мы могли выполнять умножение массива P0, P1, P2, P3 = карта(тупой.множество, [P0, P1, P2, P3]) # Параметрическая константа: 0,5 для центростремительного шлица, 0,0 для равномерного шлица, 1,0 для хордального шлица. альфа = 0.5 # Предварительно умноженная константа мощности для следующей функции tj (). альфа = альфа/2 def tj(ти, число Пи, Пиджей): xi, йи = число Пи xj, yj = Пиджей возвращаться ((xj-xi)**2 + (yj-йи)**2)**альфа + ти # Вычислить от t0 до t4 t0 = 0 t1 = tj(t0, P0, P1) t2 = tj(t1, P1, P2) t3 = tj(t2, P2, P3) # Рассчитывать только точки между P1 и P2 т = тупой.внутреннее пространство(t1, t2, nОчки) # Измените форму так, чтобы мы могли умножить на точки от P0 до P3 # и получите балл за каждое значение t. т = т.изменить форму(len(т), 1) Распечатать(т) A1 = (t1-т)/(t1-t0)*P0 + (т-t0)/(t1-t0)*P1 A2 = (t2-т)/(t2-t1)*P1 + (т-t1)/(t2-t1)*P2 A3 = (t3-т)/(t3-t2)*P2 + (т-t2)/(t3-t2)*P3 Распечатать(A1) Распечатать(A2) Распечатать(A3) B1 = (t2-т)/(t2-t0)*A1 + (т-t0)/(t2-t0)*A2 Би 2 = (t3-т)/(t3-t1)*A2 + (т-t1)/(t3-t1)*A3 C = (t2-т)/(t2-t1)*B1 + (т-t1)/(t2-t1)*Би 2 возвращаться Cdef КошкаРомЦепь(п): """ Вычислите Catmull – Rom для цепочки точек и верните комбинированную кривую. """ sz = len(п) # Кривая C будет содержать массив точек (x, y). C = [] за я в классифицировать(sz-3): c = CatmullRomSpline(п[я], п[я+1], п[я+2], п[я+3]) C.продлевать(c) возвращаться C# Определить набор точек, через которые должна пройти криваяТочки = [[0, 1.5], [2, 2], [3, 1], [4, 0.5], [5, 1], [6, 2], [7, 3]]# Вычислить сплайны Катмулла-Рома через точкиc = КошкаРомЦепь(Точки)# Преобразование точек кривой Катмулла-Рома в массивы x и y и построение графикаИкс, у = застегивать(*c)plt.участок(Икс, у)# Постройте контрольные точкиpx, ру = застегивать(*Точки)plt.участок(px, ру, 'или же')plt.Показать()Пример кода на Unity C #
с помощью UnityEngine;с помощью System.Collections;с помощью System.Collections.Generic;общественный учебный класс Катмул : MonoBehaviour { // Используйте преобразования GameObject в трехмерном пространстве в качестве ваших точек или определите массив с желаемыми точками общественный Преобразовать[] точки; // Сохраняем точки на кривой Катмулла, чтобы мы могли их визуализировать Список<Вектор2> newPoints = новый Список<Вектор2>(); // Сколько точек вы хотите на кривой uint numberOfPoints = 10; // Параметрическая константа: 0,0 для однородного сплайна, 0,5 для центростремительного сплайна, 1,0 для хордального сплайна общественный плавать альфа = 0,5f; ///////////////////////////// пустота Обновлять() { CatmulRom(); } пустота CatmulRom() { newPoints.Прозрачный(); Вектор2 p0 = точки[0].позиция; // Vector3 имеет неявное преобразование в Vector2 Вектор2 p1 = точки[1].позиция; Вектор2 p2 = точки[2].позиция; Вектор2 p3 = точки[3].позиция; плавать t0 = 0,0f; плавать t1 = GetT(t0, p0, p1); плавать t2 = GetT(t1, p1, p2); плавать t3 = GetT(t2, p2, p3); за (плавать т=t1; т<t2; т+=((t2-t1)/(плавать)numberOfPoints)) { Вектор2 A1 = (t1-т)/(t1-t0)*p0 + (т-t0)/(t1-t0)*p1; Вектор2 A2 = (t2-т)/(t2-t1)*p1 + (т-t1)/(t2-t1)*p2; Вектор2 A3 = (t3-т)/(t3-t2)*p2 + (т-t2)/(t3-t2)*p3; Вектор2 B1 = (t2-т)/(t2-t0)*A1 + (т-t0)/(t2-t0)*A2; Вектор2 Би 2 = (t3-т)/(t3-t1)*A2 + (т-t1)/(t3-t1)*A3; Вектор2 C = (t2-т)/(t2-t1)*B1 + (т-t1)/(t2-t1)*Би 2; newPoints.Добавлять(C); } } плавать GetT(плавать т, Вектор2 p0, Вектор2 p1) { плавать а = Mathf.Pow((p1.Икс-p0.Икс), 2.0f) + Mathf.Pow((p1.у-p0.у), 2.0f); плавать б = Mathf.Pow(а, альфа * 0,5f); возвращаться (б + т); } // Визуализируем точки пустота OnDrawGizmos() { Вещицы.цвет = Цвет.красный; для каждого (Вектор2 темп в newPoints) { Вектор3 позиция = новый Вектор3(темп.Икс, темп.у, 0); Вещицы.DrawSphere(позиция, 0,3f); } }}Для реализации в трехмерном пространстве после преобразования точек Vector2 в Vector3 первая строка функции GetT должна быть изменена на эту: Mathf.Pow ((p1.x-p0.x), 2.0f) + Mathf.Pow ((p1.y-p0.y), 2.0f) + Mathf.Pow ((p1.z-p0.z), 2.0f);
Пример кода в Unreal C ++
плавать GetT( плавать т, плавать альфа, const FVector& p0, const FVector& p1 ){ авто d = p1 - p0; плавать а = d | d; // Скалярное произведение плавать б = FMath::Pow( а, альфа*.5f ); возвращаться (б + т);}FVector КошкаМуллРом( const FVector& p0, const FVector& p1, const FVector& p2, const FVector& p3, плавать т / * от 0 до 1 * /, плавать альфа=.5f / * от 0 до 1 * / ){ плавать t0 = 0,0f; плавать t1 = GetT( t0, альфа, p0, p1 ); плавать t2 = GetT( t1, альфа, p1, p2 ); плавать t3 = GetT( t2, альфа, p2, p3 ); т = FMath::Лерп( t1, t2, т ); FVector A1 = ( t1-т )/( t1-t0 )*p0 + ( т-t0 )/( t1-t0 )*p1; FVector A2 = ( t2-т )/( t2-t1 )*p1 + ( т-t1 )/( t2-t1 )*p2; FVector A3 = ( t3-т )/( t3-t2 )*p2 + ( т-t2 )/( t3-t2 )*p3; FVector B1 = ( t2-т )/( t2-t0 )*A1 + ( т-t0 )/( t2-t0 )*A2; FVector Би 2 = ( t3-т )/( t3-t1 )*A2 + ( т-t1 )/( t3-t1 )*A3; FVector C = ( t2-т )/( t2-t1 )*B1 + ( т-t1 )/( t2-t1 )*Би 2; возвращаться C;}Смотрите также
Рекомендации
- ^ Кэтмелл, Эдвин; Ром, Рафаэль (1974). «Класс локальных интерполирующих сплайнов». В Барнхилле, Роберт Э .; Ризенфельд, Ричард Ф. (ред.). Компьютерный геометрический дизайн. С. 317–326. Дои:10.1016 / B978-0-12-079050-0.50020-5. ISBN 978-0-12-079050-0.
- ^ Барри, Филип Дж .; Гольдман, Рональд Н. (август 1988 г.). Рекурсивный алгоритм вычисления для класса сплайнов Катмалла – Рома. Материалы 15-й ежегодной конференции по компьютерной графике и интерактивным методам, СИГГРАФ 1988. 22. Ассоциация вычислительной техники. С. 199–204. Дои:10.1145/378456.378511.
- ^ Юксель, Джем; Шефер, Скотт; Кейзер, Джон (июль 2011 г.). «Параметризация и приложения кривых Катмалла-Рома». Системы автоматизированного проектирования. 43 (7): 747–755. CiteSeerX 10.1.1.359.9148. Дои:10.1016 / j.cad.2010.08.008.
- ^ Джен Хонг, Тан; Ачарья, У. Раджендра (2014). «Активная сплайн-модель: интерактивная сегментация на основе модели» (PDF). Цифровая обработка сигналов. 35: 64–74. arXiv:1402.6387. Дои:10.1016 / j.dsp.2014.09.002. S2CID 6953844.
внешняя ссылка
- Кривая Катмулла-Рома без изгибов и самопересечений - реализация на Java
- Кривая Катмулла-Рома без изгибов и самопересечений - упрощенная реализация на C ++
- Шлицы Catmull-Rom - интерактивная генерация через Python в блокноте Jupyter





![{ mathbf {P}} _ {i} = [x_ {i} quad y_ {i}] ^ {T}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94b787f14d85118f4669426adc26edc700fc97e7)








![t _ {{i + 1}} = left [{ sqrt {(x _ {{i + 1}} - x_ {i}) ^ {2} + (y _ {{i + 1}} - y_ {i}) ) ^ {2}}} right] ^ {{ alpha}} + t_ {i}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3fbc45aa0c46308c07c445d0e1359cafca90a17)
















![{ displaystyle mathbf {P} _ {i} = [x_ {i} quad y_ {i} quad z_ {i}] ^ {T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f8d209346f24c717009326402cc571a17b77b4)

![{ displaystyle t_ {я + 1} = left [{ sqrt {(x_ {i + 1} -x_ {i}) ^ {2} + (y_ {i + 1} -y_ {i}) ^ { 2} + (z_ {i + 1} -z_ {i}) ^ {2}}} right] ^ { alpha} + t_ {i}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4324aa06aa4fecb4a093c1fc499d931ecee8040f)

