WikiDer > Контроллер артикуляции модели мозжечка

В арифметический компьютер модели мозжечка (CMAC) - это тип нейронной сети, основанный на модели млекопитающих мозжечок. Он также известен как контроллер артикуляции модели мозжечка. Это тип ассоциативный объем памяти.[2]
CMAC был впервые предложен как средство моделирования функций для контроллеров роботов. Джеймс Альбус в 1975 г.[1] (отсюда и название), но широко использовался в обучение с подкреплением а также для автоматизированной классификации в машинное обучение сообщество. CMAC является расширением перцептрон модель. Он вычисляет функцию для входные размеры. Пространство ввода разделено на гипер-прямоугольники, каждый из которых связан с ячейкой памяти. Содержимое ячеек памяти - это веса, которые корректируются во время тренировки. Обычно используется более одного квантования пространства ввода, так что любая точка в пространстве ввода ассоциируется с рядом гипер-прямоугольников и, следовательно, с несколькими ячейками памяти. Выходные данные CMAC - это алгебраическая сумма весов всех ячеек памяти, активированных точкой ввода.
Изменение значения точки ввода приводит к изменению набора активированных гипер-прямоугольников и, следовательно, к изменению набора ячеек памяти, участвующих в выводе CMAC. Таким образом, выходные данные CMAC хранятся распределенным образом, так что выходные данные, соответствующие любой точке входного пространства, являются производными от значения, хранящегося в ряде ячеек памяти (отсюда и название ассоциативная память). Это дает обобщение.
Строительные блоки
На соседнем изображении есть два входа в CMAC, представленные как 2D-пространство. Две функции квантования были использованы для разделения этого пространства двумя перекрывающимися сетками (одна показана более жирными линиями). Один вход показан около середины, и это активировало две ячейки памяти, соответствующие заштрихованной области. Если другая точка находится рядом с показанной, она будет разделять некоторые из тех же ячеек памяти, обеспечивая обобщение.
CMAC обучается путем представления пар входных точек и выходных значений и корректировки весов в активированных ячейках на долю ошибки, наблюдаемой на выходе. Этот простой обучающий алгоритм имеет доказательство сходимости.[3]
Добавление функции ядра к гипер-прямоугольнику является нормальным, чтобы точки, падающие к краю гипер-прямоугольника, имели меньшую активацию, чем точки, падающие около центра.[4]
Одна из основных проблем, упоминаемых при практическом использовании CMAC, - это требуемый объем памяти, который напрямую связан с количеством используемых ячеек. Обычно это улучшается при использовании хеш-функция, и предоставляет память только для фактических ячеек, которые активируются входами.
Одношаговый сходящийся алгоритм
Первоначально для обновления весов CMAC используется метод наименьших средних квадратов (LMS). Конвергенция использования LMS для обучения CMAC чувствительна к скорости обучения и может привести к расхождению. В 2004 г.[5] рекурсивный алгоритм наименьших квадратов (RLS) был введен для обучения CMAC онлайн. Нет необходимости настраивать скорость обучения. Его сходимость доказана теоретически и может гарантированно сходиться за один шаг. Вычислительная сложность этого алгоритма RLS составляет O (N3).
Инфраструктура аппаратной реализации
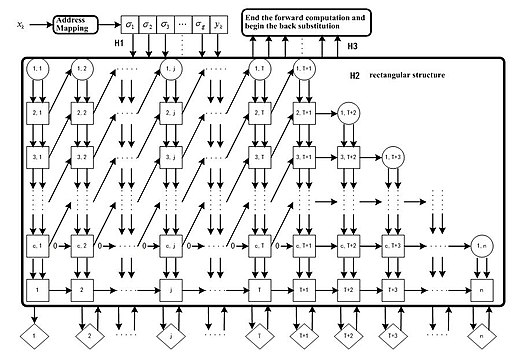
На основе QR-разложения алгоритм (QRLS) был дополнительно упрощен до сложности O (N). Следовательно, это значительно снижает использование памяти и временные затраты. Была представлена структура параллельного конвейерного массива при реализации этого алгоритма.[6]
В целом, используя алгоритм QRLS, можно гарантировать сходимость нейронной сети CMAC, а веса узлов можно обновить с помощью одного шага обучения. Его структура массива параллельных конвейеров предлагает большой потенциал для аппаратной реализации для крупномасштабного промышленного использования.
Непрерывный CMAC
Поскольку прямоугольная форма функций воспринимающего поля CMAC создает аппроксимацию прерывистой лестничной функции, путем интеграции CMAC с функциями B-сплайнов, непрерывный CMAC предлагает возможность получения любого порядка производных приближенных функций.
Глубокий CMAC
В последние годы многочисленные исследования подтвердили, что, объединяя несколько мелких структур в одну глубокую структуру, вся система может достичь лучшего представления данных и, таким образом, более эффективно справляться с нелинейными задачами высокой сложности. В 2018 г.[7] была предложена структура глубокого CMAC (DCMAC) и получен алгоритм обратного распространения ошибки для оценки параметров DCMAC. Экспериментальные результаты задачи адаптивного шумоподавления показали, что предлагаемый DCMAC может достигать лучших характеристик шумоподавления по сравнению с таковым из обычного однослойного CMAC.
Резюме
| Масштабируемость | Легко распространить на миллионы нейронов или дальше |
| Конвергенция | Обучение всегда может сходиться за один шаг |
| Производные функции | Легко получить с помощью интерполяции B-сплайнов |
| Структура оборудования | Структура параллельного конвейера |
| Использование памяти | Линейный по количеству нейронов |
| Вычислительная сложность | НА) |
Смотрите также
Рекомендации
- ^ а б J.S. Альбус (1975). «Новый подход к управлению манипулятором: контроллер артикуляции модели мозжечка (CMAC)». В: Пер. ASME, серия G. Журнал динамических систем, измерений и управления, Vol. 97. С. 220–233, 1975.
- ^ J.S. Альбус (1979). «Механизмы планирования и решения задач в мозге». В: Математические биологические науки. Vol. 45, стр. 247293, 1979.
- ^ Ю. Вонг, CMAC Learning управляется одним параметром, Международная конференция IEEE по нейронным сетям, Сан-Франциско, Vol. 1. С. 1439–43, 1993.
- ^ P.C.E. An, W.T. Miller и P.C. Паркс, Улучшения дизайна ассоциативной памяти для контроллеров артикуляции моделей мозжечка, Proc. ICANN, стр. 1207–10, 1991.
- ^ Тинг Цинь и др. «Алгоритм обучения CMAC на основе RLS». Письма о нейронной обработке 19.1 (2004): 49-61.
- ^ а б Тинг Цинь и др. «Непрерывный CMAC-QRLS и его систолический массив». Письма о нейронной обработке 22.1 (2005): 1-16.
- ^ * Yu Tsao, et al. «Адаптивное шумоподавление с использованием контроллера артикуляции модели глубокого мозжечка». IEEE Access Vol. 6. С. 37395 - 37402, 2018.
дальнейшее чтение
- Альбус, Дж. (1971). "Теория функции мозжечка". В: Математические биологические науки, Том 10, номера 1/2, февраль 1971 г., стр. 25–61
- Альбус, Дж. (1975). "Новый подход к управлению манипулятором: контроллер артикуляции модели мозжечка (CMAC)". В: Транзакции журнала ASME по динамическим системам, измерениям и управлению, Сентябрь 1975 г., стр. 220 - 227
- Альбус, Дж. (1979). "Механизмы планирования и решения проблем в мозге". В: Математические биологические науки 45, стр. 247–293, 1979.
- Цао, Ю. (2018). "Адаптивное шумоподавление с использованием контроллера артикуляции модели глубокого мозжечка". В: Доступ IEEE 6 апреля 2018 г., стр. 37395-37402.
внешняя ссылка
- Блог о контроллере артикуляции модели мозжечка (CMAC) пользователя Ting Qin. Подробнее об одношаговом конвергентном алгоритме, разработке кода и т. Д.