WikiDer > Индекс сложности - Википедия

Эта статья предоставляет недостаточный контекст для тех, кто не знаком с предметом. Пожалуйста помоги улучшить статью к обеспечение большего контекста для читателя. (Октябрь 2009 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Помимо сложности, задуманной как сложность вычисления функции (см. вычислительная сложность), в современном Информатика И в статистика еще один индекс сложности функции обозначает ее информационное содержание, что, в свою очередь, влияет на сложность изучения функция из примеров.Показатели сложности в этом смысле характеризуют весь класс функций, к которому принадлежит интересующая нас функция. Сфокусироваться на Логические функции, то деталь класса ${ displaystyle { mathsf {C}}}$ булевых функций c по существу означает, насколько глубоко артикулирован класс.

Чтобы идентифицировать этот индекс, мы должны сначала определить караульная функция из ${ displaystyle { mathsf {C}}}$. Давайте сосредоточимся на одной функции. c, назовите это концепция определен на множестве ${ displaystyle { mathcal {X}}}$ элементов, которые мы можем изобразить как точки в Евклидово пространство. В этой структуре указанная выше функция ассоциируется с c набор точек, которые, поскольку определены как внешние по отношению к концепции, препятствуют ее расширению в другую функцию ${ displaystyle { mathsf {C}}}$. Мы можем определить эти точки двояко с точки зрения определения данной концепции. c быть полностью закрытым (вторгшимся) другим концептом внутри класса. Поэтому мы называем эти точки либо часовые или же сторожевые посты; они назначаются сторожевой функцией ${ displaystyle { boldsymbol {S}}}$ к каждой концепции ${ displaystyle { mathsf {C}}}$ таким образом, что:

1. сторожевые посты находятся вне концепции c быть дозорным и внутренним по крайней мере для одного другого, включая его,
2. каждая концепция ${ displaystyle c '}$ включая c имеет хотя бы один из постов охраны c либо в промежутке между c и ${ displaystyle c '}$, или снаружи ${ displaystyle c '}$ и в отличие от постов охраны ${ displaystyle c '}$, и
3. они составляют минимальный набор с этими свойствами.

Техническое определение, взятое из (Аполлони 2006) ошибка harv: цель отсутствует: CITEREFApolloni2006 (помощь) основан на включении расширенной концепции ${ displaystyle c ^ {+}}$ состоит из c плюс его сторожевые посты другим ${ Displaystyle влево (с ' вправо) ^ {+}}$ в том же классе.

Определение сторожевой функции

Для концептуального класса ${ displaystyle { mathsf {C}}}$ на пространстве ${ displaystyle { mathfrak {X}}}$, а караульная функция это общая функция ${ displaystyle { boldsymbol {S}}: { mathsf {C}} cup { emptyset, { mathfrak {X}} } mapsto 2 ^ { mathfrak {X}}}$ удовлетворяющие следующим условиям:

1. Стражи вне дозорной концепции (${ displaystyle c cap { boldsymbol {S}} (c) = emptyset}$ для всех ${ displaystyle c in { mathsf {C}}}$).
2. Часовые находятся внутри концепции вторжения (Представив наборы ${ Displaystyle с ^ {+} = с чашка { boldsymbol {S}} (с)}$, захватническая концепция ${ displaystyle c ' in { mathsf {C}}}$ таково, что ${ displaystyle c ' not substeq c}$ и ${ displaystyle c ^ {+} substeq left (c ' right) ^ {+}}$. Обозначение ${ Displaystyle mathrm {вверх} (с)}$ набор понятий вторгается c, мы должны иметь это, если ${ displaystyle c_ {2} in mathrm {up} (c_ {1})}$, тогда ${ Displaystyle c_ {2} cap { boldsymbol {S}} (c_ {1}) neq emptyset}$).
3. ${ Displaystyle { boldsymbol {S}} (с)}$ минимальное множество с указанными выше свойствами (Нет ${ displaystyle { boldsymbol {S}} ' neq { boldsymbol {S}}}$ существует, удовлетворяющее (1) и (2) и обладающее тем свойством, что ${ Displaystyle { boldsymbol {S}} '(с) substeq { boldsymbol {S}} (с)}$ для каждого ${ displaystyle c in { mathsf {C}}}$).
4. Часовые - честные стражи. Может быть что ${ Displaystyle с substeq влево (с ' вправо) ^ {+}}$ но ${ displaystyle { boldsymbol {S}} (с) cap c '= emptyset}$ так что ${ displaystyle c ' not in mathrm {up} (c)}$. Однако это должно быть следствием того факта, что все точки ${ Displaystyle { boldsymbol {S}} (с)}$ вовлечены в настоящие дозорные c против других концепций в ${ Displaystyle mathrm {вверх} (с)}$ и не только для того, чтобы избежать включения ${ displaystyle c ^ {+}}$ к ${ Displaystyle (с ') ^ {+}}$. Таким образом, если мы удалим ${ displaystyle c ', { boldsymbol {S}} (c)}$ остается неизменной (В любое время ${ displaystyle c_ {1}}$ и ${ displaystyle c_ {2}}$ такие, что ${ displaystyle c_ {1} subset c_ {2} cup { boldsymbol {S}} (c_ {2})}$ и ${ Displaystyle c_ {2} cap { boldsymbol {S}} (c_ {1}) = emptyset}$, то ограничение ${ displaystyle { boldsymbol {S}}}$ к ${ Displaystyle {c_ {1} } чашка mathrm {up} (c_ {1}) - {c_ {2} }}$ это караульная функция на этом наборе).

${ Displaystyle { boldsymbol {S}} (с)}$ это граница из c на ${ displaystyle { boldsymbol {S}}}$.

Схематическое изображение функциональности внешнего дозорного

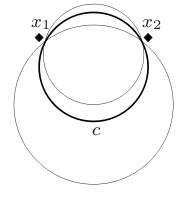
Что касается изображения справа, ${ Displaystyle {x_ {1}, x_ {2}, x_ {3} }}$ является кандидатом границы ${ displaystyle c_ {0}}$ против ${ displaystyle c_ {1}, c_ {2}, c_ {3}, c_ {4}}$. Все точки находятся в промежутке между ${ displaystyle c_ {i}}$ и ${ displaystyle c_ {0}}$. Они избегают включения ${ Displaystyle c_ {0} чашка {x_ {1}, x_ {2}, x_ {3} }}$ в ${ displaystyle c_ {3}}$, при условии, что эти точки не используются последним для самоконтроля против других концепций. Наоборот мы ожидаем, что ${ displaystyle c_ {1}}$ использует ${ displaystyle x_ {1}}$ и ${ displaystyle x_ {3}}$ как собственные стражи, ${ displaystyle c_ {2}}$ использует ${ displaystyle x_ {2}}$ и ${ displaystyle x_ {3}}$ и ${ displaystyle c_ {4}}$ использует ${ displaystyle x_ {1}}$ и ${ displaystyle x_ {2}}$ аналогично. Точка ${ displaystyle x_ {4}}$ не допускается как ${ displaystyle c_ {0}}$ сторожевой пост, поскольку, как и любое дипломатическое место, он должен располагаться вне всех других концепций, чтобы гарантировать, что он не будет занят в случае вторжения ${ displaystyle c_ {0}}$.

Определение детали

Граничный размер самого дорогостоящего концепта, подлежащего отправке с наименее эффективной функцией дозорного контроля, то есть количество

${ displaystyle mathrm {D} _ { mathsf {C}} = sup _ {{ boldsymbol {S}}, c} # { boldsymbol {S}} (c)}$,

называется деталь из ${ displaystyle { mathsf {C}}}$. ${ displaystyle { boldsymbol {S}}}$ охватывает также сторожевые функции на подмножествах ${ displaystyle { mathfrak {X}}}$ отслеживая в этом случае пересечения понятий с этими подмножествами. Собственно, собственные подмножества ${ displaystyle { mathfrak {X}}}$ могут выполнять дозорные задачи, которые оказываются сложнее, чем те, которые возникают с ${ displaystyle { mathfrak {X}}}$ сам.

Деталь ${ Displaystyle mathrm {D} _ { mathsf {C}}}$ является мерой сложности концептуальных классов, двойственных Размер ВК ${ Displaystyle mathrm {D} _ {{ mathsf {V}} C}}$. В первом случае точки используются для разделения наборов понятий, а во втором - для разделения наборов точек. В частности, имеет место следующее неравенство (Аполлони 1997) ошибка harv: цель отсутствует: CITEREFApolloni1997 (помощь)

${ Displaystyle mathrm {D} _ { mathsf {C}} leq mathrm {D} _ {{ mathsf {V}} C} +1}$

Смотрите также Радемахерская сложность для недавно введенного индекса сложности класса.

Пример: непрерывные пробелы

Учебный класс C кругов в ${ Displaystyle mathbb {R} ^ {2}}$ есть детали ${ Displaystyle mathrm {D} _ { mathsf {C}} = 2}$, как показано на рисунке слева ниже. Аналогично для класса отрезков на ${ Displaystyle mathbb {R}}$, как показано на рисунке справа.

Две точки ${ displaystyle x_ {1}, x_ {2}}$ за пределами c (толстый круг) достаточны, чтобы предотвратить его включение в больший круг, не содержащий их

Класс сегментов в ${ Displaystyle mathbb {R}}$ и два пункта, необходимые для отслеживания его концепций

Пример: дискретные пространства

Класс ${ Displaystyle { mathsf {C}} = {c_ {1}, c_ {2}, c_ {3}, c_ {4} }}$ на ${ Displaystyle { mathfrak {X}} = {x_ {1}, x_ {2}, x_ {3} }}$ концепции которых проиллюстрированы на следующей схеме, где «+» обозначает элемент ${ displaystyle x_ {j}}$ принадлежащий ${ displaystyle c_ {i}}$, «-» элемент вне ${ displaystyle c_ {i}}$ и сторожевой пост:

	${ displaystyle x_ {1}}$	${ displaystyle x_ {2}}$	${ displaystyle x_ {3}}$
${ displaystyle c_ {1} =}$	​ -⃝	​ -⃝	-
${ displaystyle c_ {2} =}$	​ -⃝	+	+
${ displaystyle c_ {3} =}$	+	​ -⃝	+
${ displaystyle c_ {4} =}$	+	+	+

Этот класс имеет ${ Displaystyle mathrm {D} _ { mathsf {C}} = 2}$. Как обычно, у нас могут быть разные дозорные функции. Худший случай S, как показано, это: ${ Displaystyle mathbf {S} (c_ {1}) = {x_ {1}, x_ {2} }, mathbf {S} (c_ {2}) = {x_ {1} }, mathbf {S} (c_ {3}) = {x_ {2} }, mathbf {S} (c_ {4}) = emptyset}$. Однако более дешевый ${ Displaystyle mathbf {S} (c_ {1}) = {x_ {3} }, mathbf {S} (c_ {2}) = {x_ {1} }, mathbf {S} (c_ {3}) = {x_ {2} }, mathbf {S} (c_ {4}) = emptyset}$:

	${ displaystyle x_ {1}}$	${ displaystyle x_ {2}}$	${ displaystyle x_ {3}}$
${ displaystyle c_ {1} =}$	-	-	​ -⃝
${ displaystyle c_ {2} =}$	​ -⃝	+	+
${ displaystyle c_ {3} =}$	+	​ -⃝	+
${ displaystyle c_ {4} =}$	+	+	+

Рекомендации

• Аполлони, В; Malchiodi, D .; Гайто, С. (2006). Алгоритмический вывод в машинном обучении. Международная серия по продвинутому интеллекту. 5 (2-е изд.). Аделаида: Мэджилл. Advanced Knowledge International
• Apolloni, B .; Кьяравалли, С. (1997). «PAC изучение концептуальных классов через границы их элементов». Теоретическая информатика. 172 (1–2): 91–120. Дои:10.1016 / S0304-3975 (95) 00240-5.