WikiDer > Вычисление циклических проверок избыточности
Вычисление циклическая проверка избыточности выводится из математики полиномиальное деление по модулю два. На практике это похоже на длинное деление из двоичный строка сообщения с фиксированным количеством добавленных нулей строкой "генераторного полинома", за исключением того, что Эксклюзивный или операции заменяют вычитания. Подобное деление эффективно реализовано аппаратно модифицированным регистр сдвига,[1] и в программном обеспечении серией эквивалентных алгоритмы, начиная с простого кода, близкого к математике, и становясь быстрее (и, возможно, более запутанный[2]) через байт-Мудрый параллелизм и пространственно-временные компромиссы.
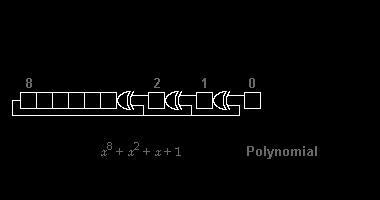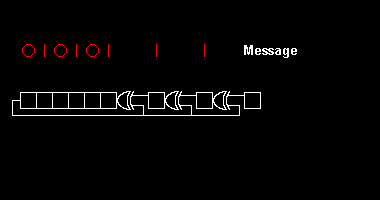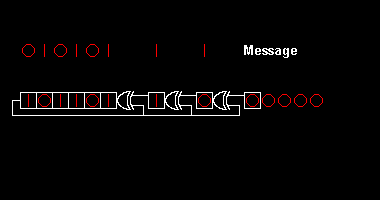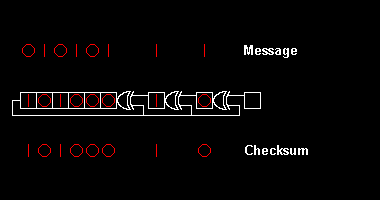

Различные стандарты CRC расширяют алгоритм полиномиального деления, определяя начальное значение регистра сдвига, последний шаг исключающего ИЛИ и, что наиболее важно, порядок битов (порядок байтов). В результате код, видимый на практике, сбивает с толку от "чистого" разделения,[2] и регистр может сдвигаться влево или вправо.
Пример
В качестве примера реализации полиномиального деления на аппаратном уровне предположим, что мы пытаемся вычислить 8-битный CRC 8-битного сообщения, состоящего из ASCII символ "W", который является двоичным 010101112, десятичная 8710, или же шестнадцатеричный 5716. Для иллюстрации мы будем использовать CRC-8-ATM (HEC) полином . Запись первого переданного бита (коэффициент наибольшей степени ) слева, это соответствует 9-битной строке «100000111».
Значение байта 5716 могут передаваться в двух разных порядках, в зависимости от используемого соглашения о порядке битов. Каждый генерирует свой многочлен сообщения . Msbit-first, это = 01010111, а lsbit-first это = 11101010. Затем их можно умножить на для создания двух 16-битных многочленов сообщений .
Затем вычисление остатка состоит из вычитания значений, кратных порождающему полиному . Это похоже на десятичное деление в столбик, но еще проще, потому что единственные возможные кратные на каждом шаге - это 0 и 1, а вычитания поручительство «из бесконечности» вместо уменьшения старших цифр. Поскольку нас не интересует частное, нет необходимости его записывать.
| Сначала старший бит | Сначала младший бит | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Обратите внимание, что после каждого вычитания биты делятся на три группы: в начале группа, которая все равна нулю; в конце - группа, не изменившаяся от оригинала; и "интересная" группа, заштрихованная синим цветом. «Интересная» группа имеет длину 8 бит, что соответствует степени полинома. На каждом шаге соответствующее кратное полинома вычитается, чтобы сделать нулевую группу на один бит длиннее, а неизмененная группа становится на один бит короче, пока не останется только последний остаток.
В примере msbit-first полином остатка равен . Преобразование в шестнадцатеричное число с использованием соглашения о том, что наибольшая степень Икс это msbit; это A216. В lsbit-first остаток равен . Преобразование в шестнадцатеричное с использованием соглашения о том, что наибольшая степень Икс это lsbit, это 1916.
Выполнение
Написание полного сообщения на каждом этапе, как это сделано в примере выше, очень утомительно. Эффективные реализации используют -кусочек регистр сдвига хранить только интересные части. Умножая многочлен на эквивалентно сдвигу регистра на одну позицию, так как коэффициенты не изменяются по значению, а только перемещаются к следующему члену полинома.
Вот первый набросок некоторых псевдокод для вычисления п-битный CRC. Он использует надуманный составной тип данных для полиномов, где Икс не целочисленная переменная, а конструктор создание Полиномиальный объект которые можно складывать, умножать и возводить в степень. К xor два полинома - сложить их по модулю два; то есть, чтобы Эксклюзивный или коэффициенты каждого члена согласования от обоих полиномов.
функция crc (битовый массив bitString [1..len], int len) {остатокПолином: = polynomialForm(bitString [1..n]) // Первые n бит сообщения // Популярный вариант дополняет здесь ОстаточноеПолиномиальное; видеть § По умолчанию -1 ниже за я из 1 к len {ОстаточныйПолином: = ОстаточныйПолином * Икс + bitString [i + n] * Икс0 // Определить bitString [k] = 0 для k> len если коэффициент Иксп остаткаПолином = 1 {остатокПолином: = остатокПолином xor generatorPolynomial}} // Популярный вариант дополняет здесь ОстаточноеПолиномиальное; видеть § Пост-инвертирование ниже возвращаться elsederPolynomial}- Фрагмент кода 1: Простое полиномиальное деление
Обратите внимание, что в этом примере кода не требуется указывать соглашение об упорядочении битов, так как не используются байты; вход bitString уже в виде битового массива, а остатокПолином обрабатывается в терминах полиномиальных операций; умножение на может быть сдвиг влево или вправо, и добавление bitString [i + n] делается для коэффициент, который может быть правым или левым концом регистра.
У этого кода есть два недостатка. Во-первых, на самом деле требуется п+ 1-битный регистр для хранения остатокПолином таким образом коэффициент можно проверить. Что еще более важно, это требует bitString быть дополненным п нулевые биты.
Первую проблему можно решить, протестировав коэффициент остатокПолином прежде чем это умножится на .
Вторую проблему можно решить, сделав последний п итераций по-разному, но есть более тонкая оптимизация, которая используется повсеместно как в аппаратной, так и в программной реализациях.
Поскольку операция XOR, используемая для вычитания полинома генератора из сообщения, является коммутативный и ассоциативный, не имеет значения, в каком порядке различные входы объединяются в остатокПолином. И, в частности, данная часть bitString не нужно добавлять в остатокПолином до самого последнего момента, когда он будет проверен, чтобы определить, следует ли xor с генераторПолином.
Это избавляет от необходимости предварительно нагружать остатокПолином с первым п биты сообщения, а также:
функция crc (битовый массив bitString [1..len], int len) {остатокПолином: = 0 // Популярный вариант дополняет здесь ОстаточноеПолиномиальное; видеть § По умолчанию -1 ниже за я из 1 к len {остатокПолином: = остатокПолином xor (битовая строка [i] * Иксп-1) если (коэффициент Иксп-1 of ОстаточныйПолином) = 1 {ОстаточныйПолином: = (ОстаточныйПолином * Икс) xor generatorPolynomial} еще {ОстаточныйПолином: = (ОстаточныйПолином * Икс) } } // Популярный вариант дополняет здесь ОстаточноеПолиномиальное; видеть § Пост-инвертирование ниже возвращаться elsederPolynomial}- Фрагмент кода 2: Полиномиальное деление с отложенным XOR сообщениями
Это стандартная аппаратная реализация CRC с побитовой обработкой, и она заслуживает изучения; как только вы поймете, почему это дает точно такой же результат, как и в первой версии, остальные оптимизации будут довольно простыми. Если остатокПолином только п бит, то коэффициенты этого и генераторПолином просто отбрасываются. Это причина того, что вы обычно видите полиномы CRC, записанные в двоичном формате, без ведущего коэффициента.
В программном обеспечении удобно отметить, что пока можно отложить xor каждого бита до самого последнего момента, это также возможно сделать раньше. Обычно удобно выполнять xor а байт за раз, даже в такой поэтапной реализации:
функция crc (байтовый массив строка [1..len], int len) {остатокПолином: = 0 // Популярный вариант дополняет здесь ОстаточноеПолиномиальное; видеть § По умолчанию -1 ниже за я из 1 к len {остатокПолином: = остатокПолином xor polynomialForm(строка [i]) * xп-8 за j из 1 к 8 { // Предполагая 8 бит на байт если коэффициент Иксп-1 остаткаПолином = 1 {ОстаточныйПолином: = (ОстаточныйПолином * Икс) xor generatorPolynomial} еще {ОстаточныйПолином: = (ОстаточныйПолином * Икс) } } } // Популярный вариант дополняет здесь ОстаточноеПолиномиальное; видеть § Пост-инвертирование ниже возвращаться elsederPolynomial}- Фрагмент кода 3: Полиномиальное деление с побайтовой XORing сообщения
Обычно это наиболее компактная программная реализация, используемая в микроконтроллеры когда пространство превыше скорости.
Порядок битов (порядок байтов)
При реализации в бит серийный аппаратное обеспечение, порождающий полином однозначно описывает назначение битов; первым переданным битом всегда является коэффициент наивысшей степени , и последнее переданные биты - это остаток CRC , начиная с коэффициента и заканчивая коэффициентом , также известный как коэффициент 1.
Однако, когда биты обрабатываются, байт за раз, например, при использовании параллельная передача, байтовое кадрирование как в Кодирование 8B / 10B или же RS-232-стиль асинхронная последовательная связь, или при реализации CRC в программного обеспечениянеобходимо указать порядок следования битов (порядок следования байтов) данных; какой бит в каждом байте считается "первым" и будет коэффициентом большей степени .
Если данные предназначены для последовательная связь, лучше всего использовать порядок битов, в который в конечном итоге будут отправлены данные. Это связано с тем, что способность CRC обнаруживать пакетные ошибки основан на близости в полиноме сообщения ; если соседние полиномиальные члены не передаются последовательно, пакет физических ошибок одной длины может рассматриваться как более длинный пакет из-за перестановки битов.
Например, оба IEEE 802 (Ethernet) и RS-232 (Серийный порт) стандарты определяют передачу в первую очередь младших битов (с прямым порядком байтов), поэтому программная реализация CRC для защиты данных, передаваемых по такому каналу, должна отображать младшие значащие биты в каждом байте с коэффициентами наивысших степеней . С другой стороны, дискеты и большинство жесткие диски сначала запишите старший бит каждого байта.
Lsbit-first CRC немного проще реализовать в программном обеспечении, поэтому встречается несколько чаще, но многие программисты считают, что упорядочение битов msbit-first проще. Так, например, XMODEM-CRC extension, раннее использование CRC в программном обеспечении, использует CRC сначала в msbit.
До сих пор псевдокод избегал указания порядка битов в байтах, описывая сдвиги в псевдокоде как умножения на и написание явных преобразований из двоичной в полиномиальную форму. На практике CRC хранится в стандартном двоичном регистре с использованием определенного соглашения об упорядочении битов. В формате «сначала мсбит» старшие двоичные биты будут отправлены первыми и, таким образом, будут содержать полиномиальные коэффициенты более высокого порядка, в то время как в форме «сначала мсбит» младшие двоичные биты содержат коэффициенты более высокого порядка. Вышеупомянутый псевдокод может быть записан в обеих формах. Для конкретности здесь используется 16-битный CRC-16-CCITT многочлен :
// Сначала старший бит (обратный порядок байтов)// x ^ 16 + x ^ 12 + x ^ 5 + 1 = (1) 0001 0000 0010 0001 = 0x1021функция crc (байтовый массив строка [1..len], int len) {rem: = 0 // Здесь популярный вариант дополняет rem за я из 1 к len {rem: = rem xor (строка [i] левый "шифт (п-8)) // n = 16 в этом примере за j из 1 к 8 { // Предполагая 8 бит на байт если rem и 0x8000 { // если установлен крайний левый (самый старший) бит rem: = (rem левый "шифт 1) xor 0x1021} еще {rem: = rem левый "шифт 1} rem: = rem и 0xffff // Обрезать остаток до 16 бит}} // Здесь популярный вариант дополняет rem возвращаться rem}- Фрагмент кода 4: деление на основе регистра сдвига, сначала старший бит
// Сначала младший бит (прямой порядок байтов)// x ^ 16 + x ^ 12 + x ^ 5 + 1 = 1000 0100 0000 1000 (1) = 0x8408функция crc (байтовый массив строка [1..len], int len) {rem: = 0 // Здесь популярный вариант дополняет rem за я из 1 к len {rem: = rem xor строка [i] за j из 1 к 8 { // Предполагая 8 бит на байт если rem и 0x0001 { // если установлен крайний правый (самый старший) бит rem: = (rem rightShift 1) xor 0x8408} еще {rem: = rem rightShift 1 } } } // Здесь популярный вариант дополняет rem возвращаться rem}- Фрагмент кода 5: деление на основе регистра сдвига, сначала младший бит
Обратите внимание, что форма lsbit-first позволяет избежать необходимости сдвигать строка [i] перед xor. В любом случае не забудьте передать байты CRC в порядке, соответствующем выбранному вами соглашению об упорядочении битов.
Многобитовые вычисления
Другая распространенная оптимизация использует Справочная таблица индексируется коэффициентами наивысшего порядка rem для обработки более одного бита дивиденда за итерацию.[3] Чаще всего используется таблица поиска с 256 записями, заменяющая внутренний цикл на j с:
// Msbit-firstrem = (rem левый "шифт 8) xor big_endian_table [строка [i] xor ((крайние левые 8 бит rem) rightShift (n-8))] // Lsbit-firstrem = (rem rightShift 8) xor little_endian_table [строка [i] xor (крайние правые 8 бит rem)]
- Фрагмент кода 6: Ядра табличного деления
Один из наиболее часто встречающихся алгоритмов CRC известен как CRC-32, используется (среди прочего) Ethernet, FDDI, ZIP и другие форматы архивов, и PNG формат изображения. Его многочлен может быть записан в msbit-first как 0x04C11DB7 или lsbit-first как 0xEDB88320. Веб-страница W3C на PNG включает приложение с короткой и простой реализацией CRC-32 на языке C на языке C.[4] Вы заметите, что этот код соответствует представленному здесь псевдокоду «первый бит за раз», а таблица создается с использованием побитового кода.
Обычно удобнее всего использовать таблицу из 256 записей, но можно использовать и другие размеры. В небольших микроконтроллерах использование таблицы с 16 записями для обработки четырех битов за раз дает полезное повышение скорости при сохранении небольшого размера таблицы. На компьютерах с достаточным объемом памяти 65536-entry table может использоваться для обработки 16 бит за раз.
Создание таблиц
Программное обеспечение для создания таблиц настолько маленькое и быстрое, что обычно быстрее вычислять их при запуске программы, чем загружать предварительно вычисленные таблицы из хранилища. Один из популярных методов - использовать побитовый код 256 раз для генерации CRC 256 возможных 8-битных байтов. Однако это можно значительно оптимизировать, воспользовавшись тем свойством, что таблица [я xor j] == таблица [i] xor таблица [j]. Только записи таблицы, соответствующие степеням двойки, необходимо вычислять напрямую.
В следующем примере кода crc имеет ценность таблица [i]:
big_endian_table [0]: = 0crc: = 0x8000 // Предполагая 16-битный полиномя: = 1делать { если crc и 0x8000 {crc: = (crc левый "шифт 1) xor 0x1021 // Полином CRC } еще {crc: = crc левый "шифт 1} // crc это ценность big_endian_table [i]; позволять j перебирать уже инициализированные записи за j из 0 к i − 1 {big_endian_table [i + j]: = crc xor big_endian_table [j]; } i: = i левый "шифт 1} пока я <256- Фрагмент кода 7: Покадровая генерация таблицы CRC, сначала MSB
little_endian_table [0]: = 0crc: = 1; i: = 128делать { если crc и 1 {crc: = (crc rightShift 1) xor 0x8408 // Полином CRC } еще {crc: = crc rightShift 1} // crc это ценность little_endian_table [я]; позволять j перебирать уже инициализированные записи за j из 0 к 255 к 2 × i {little_endian_table [i + j]: = crc xor little_endian_table [j]; } i: = i сдвиг вправо 1} пока я> 0- Фрагмент кода 8: Покадровая генерация таблицы CRC, сначала младший бит
В этих примерах кода индекс таблицы я + j эквивалентно я xor j; вы можете использовать любую удобную форму.
Байт-нарезка с использованием нескольких таблиц
Этот раздел пуст. Вы можете помочь добавляя к этому. (Август 2017 г.) |
Параллельное вычисление без таблицы
Параллельное обновление для байта или слова за раз также может выполняться явно, без таблицы.[10] Обычно это используется в реализациях высокоскоростного оборудования. Для каждого бита уравнение решается после сдвига 8 битов. В следующих таблицах перечислены уравнения для некоторых часто используемых полиномов с использованием следующих символов:
| cя | CRC бит 7… 0 (или 15… 0) перед обновлением |
| ря | CRC бит 7… 0 (или 15… 0) после обновления |
| dя | бит входных данных 7… 0 |
| ея = dя + cя | еп = e7 + е6 +… + Е1 + е0 (бит четности) |
| sя = dя + cя + 8 | sп = s7 + с6 +… + С1 + с0 (бит четности) |
| Полином: | (Икс7 + Икс3 + 1) × Икс (CRC-7-CCITT со смещением влево) | Икс8 + Икс5 + Икс4 + 1 (CRC-8-Даллас / Максим) |
|---|---|---|
| Коэффициенты: | 0x12 = (0x09 << 1) (MSBF/нормальный) | 0x8c (LSBF/обеспечить регресс) |
р0 ← г1 ← г2 ← г3 ← г4 ← г5 ← г6 ← г7 ← | 0e0 + е4 + е7е1 + е5е2 + е6е3 + е7 + е0 + е4 + е7е4 + е1 + е5е5 + е2 + е6е6 + е3 + е7 | е0 + е4 + е1 + е0 + е5 + е2 + е1е1 + е5 + е2 + е1 + е6 + е3 + е2 + е0е2 + е6 + е3 + е2 + е0 + е7 + е4 + е3 + е1е3 + е0 + е7 + е4 + е3 + е1е4 + е1 + е0е5 + е2 + е1е6 + е3 + е2 + е0е7 + е4 + е3 + е1 |
| Код C фрагменты: | uint8_t c, d, е, ж, р; … е = c ^ d; ж = е ^ (е >> 4) ^ (е >> 7); р = (ж << 1) ^ (ж << 4); | uint8_t c, d, е, ж, р; … е = c ^ d; ж = е ^ (е << 3) ^ (е << 4) ^ (е << 6); р = ж ^ (ж >> 4) ^ (ж >> 5); |
| Полином: | Икс16 + Икс12 + Икс5 + 1 (CRC-16-CCITT) | Икс16 + Икс15 + Икс2 + 1 (CRC-16-ANSI) | ||
|---|---|---|---|---|
| Коэффициенты: | 0x1021 (MSBF / нормальный) | 0x8408 (LSBF / обратный) | 0x8005 (MSBF / нормальный) | 0xa001 (LSBF / обратный) |
р0 ← г1 ← г2 ← г3 ← г4 ← г5 ← г6 ← г7 ← г8 ← г9 ← г10 ← г11 ← г12 ← г13 ← г14 ← г15 ← | s4 + с0s5 + с1s6 + с2s7 + с3 s4 s5 + с4 + с0 s6 + с5 + с1 s7 + с6 + с2c0 + с7 + с3c1 + с4c2 + с5c3 + с6c4 + с7 + с4 + с0c5 + с5 + с1c6 + с6 + с2c7 + с7 + с3 | c8 + е4 + е0c9 + е5 + е1c10 + е6 + е2c11 + е0 + е7 + е3c12 + е1c13 + е2c14 + е3c15 + е4 + е0 е0 + е5 + е1 е1 + е6 + е2 е2 + е7 + е3 е3 е4 + е0 е5 + е1 е6 + е2 е7 + е3 | sп s0 + сп s1 + с0 s2 + с1 s3 + с2 s4 + с3 s5 + с4 s6 + с5c0 + с7 + с6c1 + с7c2c3c4c5c6c7 + сп | c8 + епc9 c10c11c12c13c14 + е0c15 + е1 + е0 е2 + е1 е3 + е2 е4 + е3 е5 + е4 е6 + е5 е7 + е6 еп + е7 еп |
| Код C фрагменты: | uint8_t d, s, т; uint16_t c, р; … s = d ^ (c >> 8); т = s ^ (s >> 4); р = (c << 8) ^ т ^ (т << 5) ^ (т << 12); | uint8_t d, е, ж; uint16_t c, р; … е = c ^ d; ж = е ^ (е << 4); р = (c >> 8) ^ (ж << 8) ^ (ж << 3) ^ (ж >> 4); | uint8_t d, s, п; uint16_t c, р, т; … s = d ^ (c >> 8); п = s ^ (s >> 4); п = п ^ (п >> 2); п = п ^ (п >> 1); п = п & 1; т = п | (s << 1); р = (c << 8) ^ (т << 15) ^ т ^ (т << 1); | uint8_t d, е, п; uint16_t c, р, ж; … е = c ^ d; п = е ^ (е >> 4); п = п ^ (п >> 2); п = п ^ (п >> 1); п = п & 1; ж = е | (п << 8); р = (c >> 8) ^ (ж << 6) ^ (ж << 7) ^ (ж >> 8); |
Двухэтапное вычисление
Поскольку полином CRC-32 имеет большое количество членов, при вычислении остатка по байту за раз каждый бит зависит от нескольких бит предыдущей итерации. В аппаратных реализациях с байтовым параллелизмом это требует либо нескольких входов, либо каскадных вентилей XOR, которые Задержка распространения.
Чтобы максимизировать скорость вычислений, промежуточный остаток можно вычислить, пропустив сообщение через 123-битный регистр сдвига. Полином является тщательно подобранным кратным стандартному полиному, так что члены (отводы обратной связи) широко разнесены, и ни один бит остатка не подвергается XOR-операции более одного раза на итерацию байта. Таким образом, необходимы только двухвходовые вентили XOR, самые быстрые из возможных. Наконец, промежуточный остаток делится на стандартный полином во втором регистре сдвига, чтобы получить остаток CRC-32.[11]
Однопроходная проверка
При добавлении CRC к сообщению можно отделить переданный CRC, пересчитать его и сравнить пересчитанное значение с переданным. Однако в аппаратной части обычно используется более простой метод.
Когда CRC передается с правильным порядком байтов (соответствует выбранному соглашению об упорядочении битов), получатель может вычислить общий CRC по сообщению. и CRC, и если они верны, результат будет нулевым. Эта возможность является причиной того, что большинство сетевых протоколов, которые включают CRC, делают это. перед конечный разделитель; нет необходимости знать, приближается ли конец пакета для проверки CRC.
Варианты CRC
На практике в большинстве стандартов указывается предварительная установка регистра на все единицы и инвертирование CRC перед передачей. Это не влияет на способность CRC обнаруживать измененные биты, но дает ему возможность замечать биты, которые добавляются к сообщению.
Предустановлено на -1
Базовая математика CRC принимает (считает, как правильно переданные) сообщения, которые при интерпретации как полином являются кратными полиному CRC. Если к такому сообщению добавляются некоторые ведущие 0 бит, они не изменят его интерпретацию как полином. Это эквивалентно тому, что 0001 и 1 - это одно и то же число.
Но если передаваемое сообщение действительно заботится о начальных 0 битах, неспособность базового алгоритма CRC обнаружить такое изменение нежелательна. Если возможно, что ошибка передачи может добавить такие биты, простое решение - начать с rem регистр сдвига установлен на какое-то ненулевое значение; для удобства обычно используется значение «все единицы». Это математически эквивалентно дополнению (двоичное НЕ) первого п биты сообщения, где п - количество битов в регистре CRC.
Это никак не влияет на генерацию и проверку CRC, если и генератор, и программа проверки используют одно и то же начальное значение. Подойдет любое ненулевое начальное значение, а некоторые стандарты определяют необычные значения,[12] но значение «все единицы» (-1 в двоичном дополнительном двоичном коде) является наиболее распространенным. Обратите внимание, что однопроходная генерация / проверка CRC все равно будет давать нулевой результат, если сообщение правильное, независимо от предварительно установленного значения.
Пост-инвертировать
Такая же ошибка может возникнуть в конце сообщения, хотя и с более ограниченным набором сообщений. Добавление 0 битов к сообщению эквивалентно умножению его полинома на Икс, и если ранее оно было кратным полиному CRC, результат этого умножения также будет. Это эквивалентно тому факту, что, поскольку 726 кратно 11, 7260 равно 7260.
Аналогичное решение можно применить в конце сообщения, инвертируя регистр CRC перед его добавлением к сообщению. Опять же, подойдет любое ненулевое изменение; инвертирование всех битов (XOR с шаблоном все единицы) просто самый распространенный.
Это влияет на однопроходную проверку CRC: вместо получения нулевого результата, когда сообщение является правильным, он дает фиксированный ненулевой результат. (Чтобы быть точным, результатом является CRC (без ненулевой предустановки, но с пост-инверсией) шаблона инверсии.) Как только эта константа будет получена (проще всего выполнить однопроходную генерацию / проверку CRC для произвольное сообщение), его можно использовать напрямую для проверки правильности любого другого сообщения, проверенного с использованием того же алгоритма CRC.
Смотрите также
Общая категория
- Код исправления ошибок
- Список хеш-функций
- Паритет эквивалентен 1-битной CRC с полиномом Икс+1.
Контрольные суммы без CRC
Рекомендации
- ^ Дуброва, Елена; Мансури, Шохре Шариф (май 2012 г.). «Основанный на BDD подход к построению LFSR для параллельного кодирования CRC». Материалы международного симпозиума IEEE по многозначной логике: 128–133. ISBN 978-0-7695-4673-5.
- ^ а б Уильямс, Росс Н. (1996-09-24). "Безболезненное руководство по алгоритмам обнаружения ошибок CRC V3.00". Архивировано из оригинал на 2006-09-27. Получено 2016-02-16.
- ^ Сарвате, Дилип В. (август 1998 г.). «Вычисление циклических проверок избыточности посредством просмотра таблицы». Коммуникации ACM. 31 (8): 1008–1013. Дои:10.1145/63030.63037.
- ^ «Спецификация Portable Network Graphics (PNG) (Второе издание): Приложение D, Пример реализации кода циклического избыточного кода». W3C. 2003-11-10. Получено 2016-02-16.
- ^ Кунавис, Майкл Э .; Берри, Франк Л. (27–30 июня 2005 г.). Системный подход к созданию высокопроизводительных программных генераторов CRC (PDF). Симпозиум IEEE по компьютерам и коммуникациям 2013 г. (ISCC). Картахена, Мерсия, Испания. С. 855–862. Дои:10.1109 / ISCC.2005.18. ISBN 0-7695-2373-0.
- ^ Берри, Фрэнк Л .; Кунавис, Майкл Э. (ноябрь 2008 г.). «Новые алгоритмы поиска по таблицам для высокопроизводительной генерации CRC». Транзакции IEEE на компьютерах. 57 (11): 1550–1560. Дои:10.1109 / TC.2008.85.
- ^ Генерация высокооктанового CRC с использованием алгоритма Intel Slicing-by-8 (PDF) (Технический отчет). Intel. Архивировано из оригинал (PDF) на 2012-07-22.
- ^ Менон-Сен, Абхиджит (20 января 2017 г.). "Кто изобрел алгоритм среза по N CRC32?".
- ^ https://github.com/torvalds/linux/blob/master/Documentation/crc32.txt
- ^ Джон Буллер (1996-03-15). "Re: 8051 и CRC-CCITT". Группа новостей: comp.arch.embedded. Usenet: [email protected]. Получено 2016-02-16.
- ^ Глез, Рене Дж. (1997-01-20). «Двухэтапное вычисление циклического избыточного кода CRC-32 для сетей ATM». Журнал исследований и разработок IBM. Армонк, штат Нью-Йорк: IBM. 41 (6): 705. Дои:10.1147 / ряд 416.0705. Архивировано из оригинал на 2009-01-30. Получено 2016-02-16.
- ^ Например. низкочастотный RFID Технический паспорт TMS37157 - Пассивное низкочастотное интерфейсное устройство с EEPROM и интерфейсом транспондера 134,2 кГц (PDF), Инструменты Техаса, Ноябрь 2009 г., стр. 39, получено 2016-02-16,
Генератор CRC инициализируется значением 0x3791, как показано на рисунке 50.
внешняя ссылка
- Иоанн Павел Адамовский. «64-битный циклический избыточный код - длинное деление XOR для побайтового поиска в таблице».
- Эндрю Кадарч, Боб Дженкинс. «Эффективная (~ 1 цикл ЦП на байт) реализация CRC».















