WikiDer > Сеть глубоких убеждений
| Часть серии по |
| Машинное обучение и сбор данных |
|---|
Площадки для машинного обучения |
В машинное обучение, а сеть глубоких убеждений (DBN) это генеративный графическая модель, или, альтернативно, класс глубокий нейронная сеть, состоящий из нескольких слоев скрытые переменные («скрытые блоки») со связями между слоями, но не между блоками внутри каждого слоя.[1]
При обучении на набор примеров без присмотра, DBN может научиться вероятностно восстанавливать свои входы. Слои тогда действуют как детекторы функций.[1] После этого шага обучения DBN может быть дополнительно обучен с помощью наблюдение выполнять классификация.[2]
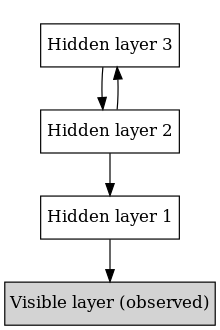
DBN можно рассматривать как набор простых неконтролируемых сетей, таких как ограниченные машины Больцмана (УКР)[1] или же автокодеры,[3] где скрытый слой каждой подсети служит видимым слоем для следующего. УКР - это ненаправленный, генеративная энергетическая модель с «видимым» входным слоем и скрытым слоем и связями между слоями, но не внутри них. Эта композиция приводит к быстрой пошаговой процедуре обучения без учителя, где контрастное расхождение применяется к каждой подсети по очереди, начиная с «самой нижней» пары слоев (самый низкий видимый слой - это Обучающий набор).
Наблюдение[2] что DBN можно обучить жадно, по одному слою за раз, привело к одному из первых эффективных глубокое обучение алгоритмы.[4]:6 В целом существует множество привлекательных реализаций и вариантов использования DBN в реальных приложениях и сценариях (например, электроэнцефалография,[5] открытие лекарств[6][7][8]).
Обучение персонала

Метод обучения RBM, предложенный Джеффри Хинтон для использования с обучением модели «Продукт эксперта» контрастное расхождение (CD).[9] CD дает приближение к максимальная вероятность метод, который идеально подходит для обучения весам.[10][11] При обучении одного RBM обновления веса выполняются с градиентный спуск с помощью следующего уравнения:
куда, это вероятность видимого вектора, которая определяется как . - статистическая сумма (используется для нормализации) и - функция энергии, присвоенная состоянию сети. Более низкая энергия указывает на то, что сеть находится в более «желательной» конфигурации. Градиент имеет простую форму куда представляют собой средние по распределению . Проблема возникает при отборе проб потому что это требует расширенного чередования Выборка Гиббса. Компакт-диск заменяет этот шаг выполнением попеременного семплирования Гиббса для шаги (значения выступить хорошо). После шаги, данные выбираются, и этот образец используется вместо . Процедура CD работает следующим образом:[10]
- Инициализируйте видимые единицы тренировочным вектором.
- Обновите скрытые блоки параллельно с учетом видимых блоков: . это сигмовидная функция и это предвзятость .
- Обновите видимые блоки параллельно с учетом скрытых блоков: . это предвзятость . Это называется этапом «реконструкции».
- Повторно обновите скрытые блоки параллельно с учетом реконструированных видимых блоков, используя то же уравнение, что и на шаге 2.
- Выполните обновление веса: .
Как только RBM обучен, другой RBM «накладывается» поверх него, принимая входные данные от последнего обученного слоя. Новый видимый слой инициализируется обучающим вектором, а значения единиц в уже обученных слоях назначаются с использованием текущих весов и смещений. Затем новый RBM обучается с помощью описанной выше процедуры. Весь этот процесс повторяется до тех пор, пока не будет достигнут желаемый критерий остановки.[12]
Хотя приближение CD к максимальной вероятности является грубым (не следует за градиентом какой-либо функции), оно эмпирически эффективно.[10]
Смотрите также
Рекомендации
- ^ а б c Хинтон Г (2009). "Сети глубоких убеждений". Scholarpedia. 4 (5): 5947. Bibcode:2009SchpJ ... 4.5947H. Дои:10.4249 / scholarpedia.5947.
- ^ а б Hinton GE, Osindero S, Teh YW (июль 2006 г.). «Алгоритм быстрого обучения для сетей глубоких убеждений» (PDF). Нейронные вычисления. 18 (7): 1527–54. CiteSeerX 10.1.1.76.1541. Дои:10.1162 / neco.2006.18.7.1527. PMID 16764513.
- ^ Бенжио Y, Ламблин П., Поповичи Д., Ларошель Х (2007). Жадное послойное обучение глубоких сетей (PDF). НИПС.
- ^ Бенджио, Ю. (2009). «Изучение глубинных архитектур для ИИ» (PDF). Основы и тенденции в машинном обучении. 2: 1–127. CiteSeerX 10.1.1.701.9550. Дои:10.1561/2200000006.
- ^ Movahedi F, Coyle JL, Sejdic E (май 2018 г.). "Сети глубокого убеждения для электроэнцефалографии: обзор недавних результатов и перспектив на будущее". Журнал IEEE по биомедицинской и медицинской информатике. 22 (3): 642–652. Дои:10.1109 / jbhi.2017.2727218. ЧВК 5967386. PMID 28715343.
- ^ Гасеми, Перес-Санчес; Мери, Перес-Гарридо (2018). «Нейронные сети и алгоритмы глубокого обучения, используемые в исследованиях QSAR: достоинства и недостатки». Открытие наркотиков сегодня. 23 (10): 1784–1790. Дои:10.1016 / j.drudis.2018.06.016. PMID 29936244.
- ^ Гасеми, Перес-Санчес; Мехри, фассихи (2016). «Роль различных методов отбора проб в улучшении прогнозирования биологической активности с использованием сети глубокого убеждения». Журнал вычислительной химии. 38 (10): 1–8. Дои:10.1002 / jcc.24671. PMID 27862046.
- ^ Gawehn E, Hiss JA, Schneider G (январь 2016 г.). «Глубокое обучение в открытии лекарств». Молекулярная информатика. 35 (1): 3–14. Дои:10.1002 / мин.201501008. PMID 27491648.
- ^ Хинтон Г.Е. (2002). «Обучающий продукт для экспертов путем минимизации противоречивых расхождений» (PDF). Нейронные вычисления. 14 (8): 1771–1800. CiteSeerX 10.1.1.35.8613. Дои:10.1162/089976602760128018. PMID 12180402.
- ^ а б c Хинтон Г.Е. (2010). «Практическое руководство по обучению ограниченных машин Больцмана». Tech. Представитель UTML TR 2010-003.
- ^ Фишер А., Игель С. (2014). «Обучение ограниченным машинам Больцмана: Введение» (PDF). Распознавание образов. 47: 25–39. CiteSeerX 10.1.1.716.8647. Дои:10.1016 / j.patcog.2013.05.025. Архивировано из оригинал (PDF) на 2015-06-10. Получено 2017-07-02.
- ^ Бенджио Y (2009). «Изучение глубинных архитектур для ИИ» (PDF). Основы и тенденции в машинном обучении. 2 (1): 1–127. CiteSeerX 10.1.1.701.9550. Дои:10.1561/2200000006. Архивировано из оригинал (PDF) на 2016-03-04. Получено 2017-07-02.
внешняя ссылка
- "Сети глубокого убеждения". Учебники по глубокому обучению.
- "Пример сети глубокого убеждения". Deeplearning4j Учебники. Архивировано из оригинал на 2016-10-03. Получено 2015-02-22.



















