WikiDer > Граф Дейтера
| Граф Дейтера | |
|---|---|
 | |
| Вершины | 112 |
| Края | 336 |
| Радиус | 7 |
| Диаметр | 7 |
| Обхват | 6 |
| Автоморфизмы | 2688 |
| Таблица графиков и параметров | |
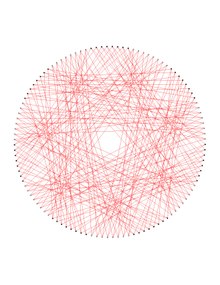
в математический поле теория графов, то Граф Дейтера 6-регулярный граф со 112 вершинами, 336 ребрами и обхватом 6.[1][2][3][4][5][6][7] График Дейтера получается путем удаления копии Код Хэмминга длины 7 из двоичногокуб.
Граф Дейтера и, соответственно, любой граф, полученный удалением Код Хэмминга длины 2р-1 из (2р-1)-куб, это симметричный графВ частности, граф Дейтера допускает 3-факторизация на две копии Любляна график, который является третьим по величине из существующих полусимметричный кубический граф регулярной степени 3. Обхват графа Любляны равен 10.
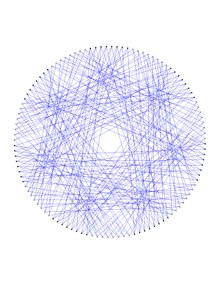
Фактически, доказано, что граф Дейтера может быть двухцветным, скажем, в наборе цветов {красный, синий}, как на верхнем рисунке справа, так что получающиеся в результате монохроматические по краям красный и синий покрывающие вершины подграфы являются копиями Любляна график. Эти две копии содержат ровно 112 вершин графа Дейтера и по 168 ребер каждая, причем обе копии имеют обхват 10, в то время как граф Дейтера имеет обхват 6 и обхват 7-куба 4. Кажется, что граф Дейтера наименьший. симметричный граф имеющий связную самодополняющую вершинно-остовную полусимметричный кубический подграф.
И красный, и синий подграфы Любляны, покрывающие вершины, графа Дейтера могут быть представлены как покрывающие графы из График Хивуда, а именно как 8-обложки График Хивуда. Это предлагается в каждом из двух представлений Любляна график(красный вверху, синий внизу, оба вправо), поочередно раскрашивая прообразы последовательных вершин График Хивуда, скажем, в черно-белом (лучше просмотреть, дважды щелкнув изображение для увеличения рисунка), согласно График Хивуда раздвоение. Каждый такой инверсный образ формируется 8 соседями, вдоль фиксированного координатного направления 7-куба, половины кода Хэмминга, имеющего фиксированный вес, 0 или 1. Путем обмена этими весами посредством перестановки (0 1), можно перейти от смежности, предлагаемой красным графом Любляны, к соседству, предлагаемому синим графом Любляны, или наоборот.
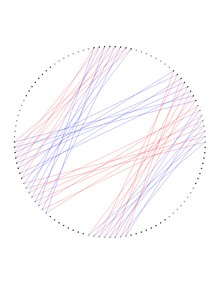
Одна седьмая часть графика Дейтера представлена на отдельном рисунке внизу, который может быть получен из двух полученных копий График Хивуда.
использованная литература
- ^ Клин М .; Лаури Дж .; Зив-Ав М. "Связи двух полусимметричных графов на вершинах через призму ассоциативных схем", Jour. SymbolicComput., 47–10, 2012, 1175–1191.
- ^ Borges J .; Дейтер И. Дж. «О совершенных доминирующих множествах в гиперкубах и их дополнениях», Дж. Комбин. Математика. Комбинировать. Comput.20 (1996), 161-173
- ^ Дейтер И. Дж. «О симметричных подграфах 7-куба: обзор», Дискретная математика. 124 (1994) 55–66
- ^ Дейтер И. Дж. "Симметрия факторов 7-куба Хэммингшелла", J. Combin. Des. 5 (1997), 301–309
- ^ Дейтер И. Дж.; Гуан П. «Подмножества ребер с блокировкой квадратов в гиперкубах и устранение вершин», Теория графов, комбинаторика, алгоритмы и приложения (Сан-Франциско, Калифорния, 1989), 162–174, SIAM, Филадельфия, Пенсильвания, 1991
- ^ Дейтер И. Дж .; Пуйоль Дж. «Совершенное доминирование и симметрия в гиперкубах», Труды Двадцать шестой Юго-Восточной международной конференции по комбинаторике, теории графов и вычислениям (Бока-Ратон, Флорида, 1995). Congr. Нумер. 111 (1995), 18–32
- ^ Дейтер И. Дж .; Weichsel P.M. "Скрученные перфектдоминирующие подграфы гиперкубов", Труды Двадцать четвертой Юго-Восточной международной конференции по комбинаторике, теории графов и вычислениям (Бока-Ратон, Флорида, 1993) .Congr. Нумер. 94 (1993), 67–78.