WikiDer > Меры расстояния (космология)

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. Найдите источники: Космология "мер расстояния" – Новости · газеты · книги · ученый · JSTOR (Апрель 2018 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Часть серии по
Физическая космология
Большой взрыв · Вселенная Возраст вселенной Хронология Вселенной
Ранняя вселенная Эпоха Планка Эпоха великого объединения Электрослабая эпоха Кварковая эпоха Адронная эпоха Лептонная эпоха Фотонная эпоха Нуклеосинтез Большого взрыва Инфляция Темные времена Звездная эра Фоны Космический фоновый радиационный фон (CBR) Фон гравитационных волн (ФГВ) Космический микроволновый фон (CMB) · Космический нейтринный фон (CNB) Космический инфракрасный фон (ИНБ)
Расширение· Будущее Закон Хаббла · Красное смещение Расширение Вселенной Ускоряющееся расширение Вселенной Сопутствующие и правильные расстояния Метрика FLRW · Уравнения Фридмана Неоднородная космология Будущее расширяющейся Вселенной Конечная судьба вселенной Тепловая смерть вселенной Большой разрыв Большой хруст Большой отскок
Составные части· Структура Составные части Лямбда-CDM модель Барионная материя Экзотическая материя Энергия Отрицательная энергия Нулевая энергия Энергия вакуума Радиация Фоновое излучение Темная энергия Квинтэссенция Фантомная энергия Темная материя Холодная темная материя Теплая темная материя Смешанная темная материя Горячая темная материя Светлая темная материя Самовзаимодействующая темная материя Скалярное поле темная материя Темное излучение Темная жидкость Зеркальное дело Структура Форма вселенной Реионизация · Формирование структуры Формирование галактики Крупномасштабная конструкция Большая группа квазаров Нить галактики Сверхскопление Скопление галактик Группа галактик Местная группа Галактика Ореол темной материи Звездное скопление Солнечная система Планетная система Пустота
Эксперименты Бумеранг Исследователь космического фона (COBE) Обзор темной энергии Евклид Проект Illustris Обсерватория Веры К. Рубин Космическая обсерватория Планка Слоан цифровой обзор неба (SDSS) Обзор красного смещения галактики 2dF ("2dF") ВселеннаяМашина Микроволновая анизотропия Уилкинсона Зонд (WMAP)
Ученые Ааронсон Альфвен Альфер Бхарадвадж Коперник де Ситтер Дике Эддингтон Элерс Эйнштейн Эллис Фридман Галилео Гамов Guth Хаббл Лемэтр Linde Mather Ньютон Penzias Вбивать в голову Шмидт Шварцшильд Гладкий Старобинский Steinhardt Suntzeff Сюняев Толман Уилсон Зельдович
История темы Открытие космического микроволн фоновое излучение История теории большого взрыва Религиозные интерпретации теория большого взрыва Хронология космологических теорий
Категория  Астрономический портал
v т е

Меры расстояния используются в физическая космология дать естественное представление о расстояние между двумя объектами или событиями в вселенная. Их часто используют для завязывания наблюдаемый количество (например, яркость далекого квазар, то красное смещение далекого галактика, или угловой размер акустических пиков в CMB спектр мощности) на другую величину, которая не напрямую наблюдаемый, но более удобный для расчетов (например, сопутствующие координаты квазара, галактики и т. д.). Все обсуждаемые здесь меры расстояния сводятся к общему понятию Евклидово расстояние при малом красном смещении.

В соответствии с нашим нынешним пониманием космологии, эти меры рассчитываются в контексте общая теория относительности, где Фридман – Лемэтр – Робертсон – Уокер Решение используется для описания Вселенной.

Обзор

В космологии существует несколько различных определений «расстояния», которые все совпадают для достаточно малых красные смещения. Выражения для этих расстояний наиболее практичны, когда они записываются как функции красного смещения. ${displaystyle z}$, так как красное смещение всегда наблюдается. Их легко записать как функции от масштаб ${displaystyle a = 1 / (1 + z)}$, космическое время ${displaystyle t}$ или же конформное время ${displaystyle eta}$ а также путем простого преобразования переменных. Определив безразмерный Параметр Хаббла и расстояние Хаббла ${displaystyle d_ {H} = c / H_ {0}}$, связь между разными расстояниями становится очевидной.

${displaystyle E (z) = {sqrt {Omega _ {r} (1 + z) ^ {4} + Omega _ {m} (1 + z) ^ {3} + Omega _ {k} (1 + z) ^ {2} + Омега _ {Лямбда}}}}$

Здесь, ${displaystyle Omega _ {r}}$ - полная плотность энергии излучения, ${displaystyle Omega _ {m}}$ полная плотность вещества, ${displaystyle Omega _ {Lambda}}$ это темная энергия плотность, ${displaystyle Omega _ {k} = 1-Omega _ {m} -Omega _ {Lambda}}$ представляет кривизну, ${displaystyle H_ {0}}$ - это параметр Хаббла сегодня и ${displaystyle c}$ это скорость света. В Параметр Хаббла при данном красном смещении тогда ${displaystyle H (z) = H_ {0} E (z)}$.

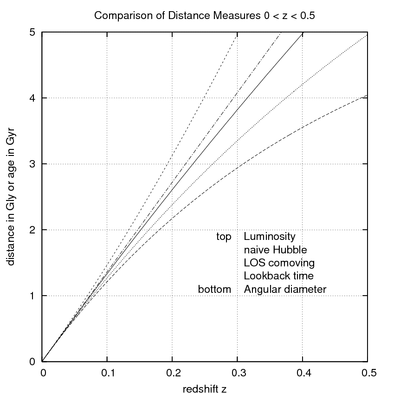
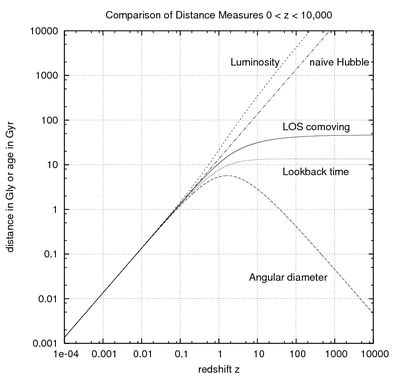
Чтобы вычислить расстояние до объекта по его красному смещению, мы должны интегрировать приведенное выше уравнение. Хотя для некоторых ограниченных вариантов выбора параметров (например, только материя: ${displaystyle Omega _ {m} = Omega _ {mathrm {total}} = 1}$) сопутствующий интеграл расстояний, определенный ниже, имеет замкнутый аналитический вид, в общем, и в частности для параметры нашей Вселенной- мы можем только найти решение численно. Космологи обычно используют следующие меры для измерения расстояний от наблюдателя до объекта при красном смещении. ${displaystyle z}$ по прямой видимости:^[1]

Сопутствующее расстояние:

${displaystyle d_ {C} (z) = d_ {H} int _ {0} ^ {z} {frac {dz '} {E (z')}}}$

Где здесь ${displaystyle d_ {H}}$ расстояние Хаббла, определяемое как скорость света, умноженная на время Хаббла; ${displaystyle d_ {H} = c / H_ {0} = 3000h ^ {- 1} {ext {Mpc}} = 9,26cdot 10 ^ {25} h ^ {- 1} {ext {m}}}$.

Поперечное сопутствующее расстояние:

${displaystyle d_ {M} (z) = left {{egin {array} {ll} {frac {d_ {H}} {sqrt {Omega _ {k}}}} sinh left ({sqrt {Omega _ {k}) }} d_ {C} (z) / d_ {H} ight) & {ext {for}} Omega _ {k}> 0 d_ {C} (z) & {ext {for}} Omega _ {k} = 0 {frac {d_ {H}} {{sqrt {| Omega _ {k}}} |}} sin left ({sqrt {| Omega _ {k} |}} d_ {C} (z) / d_ {H} ight) & {ext {for}} Omega _ {k} <0end {array}} ight.}$

Расстояние углового диаметра:

${displaystyle d_ {A} (z) = {гидроразрыв {d_ {M} (z)} {1 + z}}}$

Расстояние яркости:

${displaystyle d_ {L} (z) = (1 + z) d_ {M} (z)}$

Расстояние света:

${displaystyle d_ {T} (z) = d_ {H} int _ {0} ^ {z} {frac {dz '} {(1 + z') E (z ')}}}$

Обратите внимание, что сопутствующее расстояние восстанавливается из поперечного сопутствующего расстояния путем принятия предела ${displaystyle Omega _ {k} o 0}$, такая, что две меры расстояния эквивалентны в плоская вселенная.

Возраст вселенной ${displaystyle lim _ {zightarrow infty} d_ {T} (z) / c}$, а время, прошедшее с момента красного смещения ${displaystyle z}$ до сих пор

${displaystyle t (z) = d_ {T} (z) / c}$

Сравнение космологических расстояний, от нулевого красного смещения до красного смещения 0,5. Фоновая космология - параметр Хаббла 72 км / с / Мпк, ${displaystyle Omega _ {Lambda} = 0,732}$, ${displaystyle Omega _ {m {материя}} = 0,266}$, ${displaystyle Omega _ {m {радиация}} = 0,266 / 3454}$, и ${displaystyle Omega _ {k}}$ выбрано так, чтобы сумма параметров Омега была равна 1.

Сравнение космологических мер расстояния, от нулевого красного смещения до красного смещения 10 000, соответствующих эпохе равенства материи и излучения. Фоновая космология - параметр Хаббла 72 км / с / Мпк, ${displaystyle Omega _ {Lambda} = 0,732}$, ${displaystyle Omega _ {m {материя}} = 0,266}$, ${displaystyle Omega _ {m {радиация}} = 0,266 / 3454}$, и ${displaystyle Omega _ {k}}$ выбирается так, чтобы сумма параметров Omega была равна единице.

Альтернативная терминология

Пиблз (1993) называет поперечное сопутствующее расстояние «расстоянием углового размера», которое не следует принимать за расстояние углового диаметра.^[2] Несмотря на то, что это не вопрос номенклатуры, поперечное сопутствующее расстояние эквивалентно расстоянию собственного движения, которое определяется как отношение поперечной скорости к его собственному движению в радианах за время. Иногда символы ${displaystyle chi}$ или же ${displaystyle r}$ используются для обозначения как сопутствующего, так и углового диаметра. Иногда расстояние, пройденное светом, также называют «ретроспективным расстоянием».

Подробности

Сопутствующее расстояние

Сопутствующее расстояние между фундаментальными наблюдателями, то есть наблюдателями, которые оба движутся вместе с Хаббловский поток, не меняется со временем, так как сопутствующие расстояния объясняют расширение Вселенной. Сопутствующее расстояние получается путем интегрирования соответствующих расстояний до ближайших фундаментальных наблюдателей вдоль луча зрения (LOS), где правильное расстояние - это то, что даст измерение при постоянном космическом времени.

В стандартная космология, сопутствующее расстояние и правильное расстояние это две тесно связанные меры расстояния, используемые космологами для измерения расстояний между объектами; сопутствующее расстояние - это правильное расстояние в настоящее время.

Правильное расстояние

Правильное расстояние примерно соответствует тому, где удаленный объект мог бы находиться в определенный момент времени. космологическое время, который со временем может измениться из-за расширение вселенной. Сопутствующее расстояние учитывает расширение Вселенной, что дает расстояние, которое не изменяется во времени из-за расширения пространства (хотя это может измениться из-за других, локальных факторов, таких как движение галактики внутри скопления); сопутствующее расстояние - это правильное расстояние в настоящее время.

Поперечное сопутствующее расстояние

Два движущихся объекта с постоянным красным смещением ${displaystyle z}$ которые разделены углом ${displaystyle delta heta}$ в небе есть расстояние ${displaystyle delta heta d_ {M} (z)}$, где поперечное сопутствующее расстояние ${displaystyle d_ {M}}$ определяется соответствующим образом.

Расстояние углового диаметра

Объект размера ${displaystyle x}$ при красном смещении ${displaystyle z}$ который имеет угловой размер ${displaystyle delta heta}$ имеет расстояние углового диаметра ${displaystyle d_ {A} (z) = x / delta heta}$. Обычно это используется для наблюдения так называемого стандартные линейки, например, в контексте барионные акустические колебания.

Расстояние яркости

Если внутренняя яркость ${displaystyle L}$ удаленного объекта известно, мы можем вычислить его световое расстояние, измерив поток ${displaystyle S}$ и определить ${displaystyle d_ {L} (z) = {sqrt {L / 4pi S}}}$, что оказывается эквивалентным приведенному выше выражению для ${displaystyle d_ {L} (z)}$. Эта величина важна для измерения стандартные свечи подобно сверхновые типа Ia, которые впервые были использованы для обнаружения ускорения расширение вселенной.

Расстояние света

Это расстояние - это время (в годах), которое потребовалось свету, чтобы достичь наблюдателя от объекта, умноженное на скорость света. Например, радиус наблюдаемая вселенная в этом случае мера расстояния становится возрастом Вселенной, умноженным на скорость света (1 световой год / год), то есть 13,8 миллиарда световых лет. Также см заблуждения размером с видимую Вселенную.

Двойственность расстояний Этерингтона

Уравнение двойственности расстояния Этерингтона ^[3] - это соотношение между светимостью стандартных свечей и расстоянием по угловому диаметру. Это выражается следующим образом: ${displaystyle d_ {L} = (1 + z) ^ {2} d_ {A}}$

Смотрите также

• Большой взрыв
• Сопутствующее расстояние
• Уравнения Фридмана
• Парсек
• Физическая космология
• Лестница космических расстояний
• Метрика Фридмана-Лемэтра-Робертсона-Уокера
• Субатомный масштаб

Рекомендации

• Скотт Додельсон, Современная космология. Академическая пресса (2003).

внешняя ссылка

• «Шкала расстояний до Вселенной» сравнивает различные космологические меры расстояния.
• 'Меры расстояния в космологии' подробно объясняет, как рассчитать различные меры расстояния в зависимости от модели мира и красного смещения.
• iCosmos: Космологический калькулятор (с построением графиков) вычисляет различные меры расстояния как функцию космологической модели и красного смещения и генерирует графики для модели от красного смещения от 0 до 20.