WikiDer > Додекаэдрическая призма
| Додекаэдрическая призма | |
|---|---|
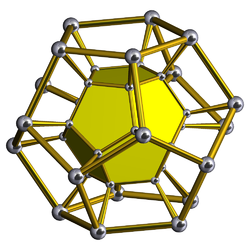 Диаграмма Шлегеля Показана только одна додекаэдрическая ячейка | |
| Тип | Призматический однородный 4-многогранник |
| Единый индекс | 57 |
| Символ Шлефли | т0,3{5,3,2} или {5,3} × {} |
| Кокстер-Дынкин | |
| Клетки | 2 (5.5.5) 12 (4.4.5) |
| Лица | 30 {4} 24 {5} |
| Края | 80 |
| Вершины | 40 |
| Фигура вершины | 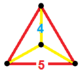 Равносторонне-треугольная пирамида |
| Группа симметрии | [5,3,2], заказ 240 |
| Характеристики | выпуклый |
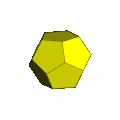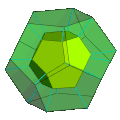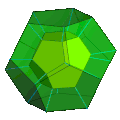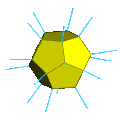
В геометрия, а додекаэдрическая призма выпуклый равномерный 4-многогранник. Этот 4-многогранник имеет 14 многогранник ячеек: 2 додекаэдр соединены 12 пятиугольные призмы. У него 54 лица: 30 квадратов и 24 пятиугольника. У него 80 ребер и 40 вершин.
Его можно построить, создав два совпадающих додекаэдра в 3-м пространстве и переведя каждую копию в противоположных перпендикулярных направлениях в 4-м пространстве, пока их расстояние не станет равным длине их ребер.
Это один из 18 выпуклых однородные многогранные призмы создан с использованием униформы призмы для соединения пар параллельно Платоновы тела или Архимедовы тела.
Альтернативные названия
- Додекаэдрическая диадическая призма Норман В. Джонсон
- Допинг (для додекаэдрической призмы) Джонатан Бауэрс
- Додекаэдрическая гиперпризма
Изображений
Прозрачный Диаграмма Шлегеля
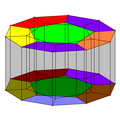
An орфографическая проекция с каркасной моделью и имеет половину пятиугольных граней, окрашенных, чтобы показать два додекаэдра. Додекаэдры правильные, но выглядят уплощенными из-за проекции и направления взгляда.
Структура
Додекаэдрическая призма состоит из двух додекаэдров, соединенных между собой 12 пятиугольник призмы. Пятиугольные призмы соединены друг с другом квадратными гранями.
Прогнозы
Ортографическая проекция додекаэдрической призмы в трехмерное пространство, расположенная впереди пятиугольной призмы, имеет десятиугольный конверт (см. схему). Две пятиугольные призмы выступают в центр этого объема, каждая окружена пятью другими пятиугольными призмами. Они образуют два набора (каждый из которых состоит из центральной пятиугольной призмы, окруженной 5 другими неоднородными пятиугольными призмами), которые дважды покрывают объем десятиугольной призмы. Два додекаэдра выступают на десятиугольные грани оболочки.
Ортографическая проекция додекаэдра сначала додекаэдром в трехмерное пространство имеет додекаэдрическую огибающую. Две додекаэдрические ячейки проецируются на весь объем этой оболочки, в то время как 12 декагональных призматических ячеек выступают на ее 12 пятиугольных гранях.
внешняя ссылка
- 6. Выпуклая однородная призматическая полихора - Модель 57., Георгий Ольшевский.
- Клитцинг, Ричард. "4D однородные многогранники (полихоры) x o3o5x - dope".