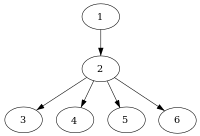
WikiDer > Доминатор (теория графов)
| 1 | дом | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 2 | дом | 2 | 3 | 4 | 5 | 6 | |
| 3 | дом | 3 | |||||
| 4 | дом | 4 | |||||
| 5 | дом | 5 | |||||
| 6 | дом | 6 | |||||
| Соответствующее отношение господства | |||||||
| Серые узлы не строго доминируют | |||||||
| Красные узлы немедленно доминируют | |||||||
В Информатика, в графики потока управления, а узел d доминирует узел п если каждый путь от входной узел к п должен пройти d. Условно это записывается как d дом п (или иногда d п). По определению, каждый узел доминирует над собой.
Есть ряд связанных понятий:
- Узел d строго доминирует узел п если d доминирует п и d не равно п.
- В непосредственный господин или идом узла п единственный узел, который строго доминирует п но не доминирует строго над любым другим узлом, который строго доминирует п. У каждого узла, кроме входного, есть непосредственный доминант.[1]
- В граница господства узла d это набор всех узлов п такой, что d доминирует над непосредственным предшественником п, но d не строго доминирует п. Это набор узлов, где d 's доминирование прекращается.
- А дерево доминирования это дерево где дочерние элементы каждого узла - это те узлы, над которыми он непосредственно доминирует. Поскольку непосредственный господин уникален, это дерево. Начальный узел - это корень дерева.
История
Доминирование было впервые представлено Риз Т. Проссер в статье 1959 года об анализе блок-схем.[2] Проссер не представил алгоритм для вычисления доминирования, который пришлось ждать десять лет Эдварду С. Лоури и К. У. Медлоку.[3] Рон Ситрон и другие. возродили интерес к доминированию в 1989 г., когда они применили его к проблеме эффективного вычисления размещения функций φ, которые используются в статическая форма единого назначения.[4]
Приложения
Доминаторы, и особенно границы доминирования, находят применение в компиляторы для вычислений статическая форма единого назначения. Некоторые оптимизации компилятора также могут выиграть от доминирования. Блок-граф в этом случае включает базовые блоки.
Автоматическое распараллеливание выигрывает от границ постдоминирования. Это эффективный метод вычисления зависимости управления, который имеет решающее значение для анализа.
Для анализа использования памяти может быть полезно использовать дерево доминирования, чтобы легко находить утечки и определять высокий уровень использования памяти.[5]
В аппаратных системах доминирующие элементы используются для вычисления вероятностей сигналов для генерации тестов, оценки коммутационных действий для анализа мощности и шума и выбора точек отсечки при проверке эквивалентности.[6]В программных системах они используются для уменьшения размера набора тестов в таких методах структурного тестирования, как покрытие операторов и переходов.[7]
Алгоритмы
Доминаторы узла n задаются максимальным решением следующих уравнений потока данных:
где - начальный узел.
Доминатором начального узла является сам начальный узел. Набор доминаторов для любого другого узла n - это пересечение набора доминаторов для всех предшественников p из n. Узел n также входит в набор доминаторов для n.
Алгоритм прямого решения:
// доминирующим элементом начального узла является сам старт Dom (n0) = {n0} // для всех остальных узлов устанавливаем все узлы как доминирующие для каждого п в N - {n0} Dom (n) = N; // итеративно удаляем узлы, которые не являются доминирующими в то время как изменения в любом Dom (n) для каждого п в N - {n0}: Dom (n) = {n} объединение с пересечением над Dom (p) для всех p в pred (n)Прямое решение квадратичный по количеству узлов, или O (п2). Ленгауэр и Tarjan разработал алгоритм, который является почти линейным,[1] и на практике, за исключением нескольких искусственных графов, алгоритм и его упрощенная версия так же быстры или быстрее, чем любой другой известный алгоритм для графов всех размеров, и его преимущество увеличивается с размером графа.[8]
Кейт Д. Купер, Тимоти Дж. Харви и Кен Кеннеди из Университет Райса описать алгоритм, который по существу решает приведенные выше уравнения потока данных, но использует хорошо спроектированные структуры данных для повышения производительности.[9]
Постдоминирование
Как и в приведенном выше определении доминирования, узел z говорят пост-доминировать узел п если все пути к выходному узлу графа начинаются с п должен пройти z. Точно так же непосредственный пост-доминатор узла п постдоминатор п это не строго постдоминирует с другими строгими постдоминаторами п.
Смотрите также
использованная литература
- ^ а б Ленгауэр, Томас; Тарджан, Роберт Эндре (Июль 1979 г.). «Быстрый алгоритм поиска доминаторов в потоковом графе». Транзакции ACM по языкам и системам программирования. 1 (1): 121–141. CiteSeerX 10.1.1.117.8843. Дои:10.1145/357062.357071.
- ^ Проссер, Риз Т. (1959). «Приложения булевых матриц к анализу блок-схем». Совместные компьютерные конференции AFIPS: доклады, представленные на 1–3 декабря 1959 г., Восточная объединенная компьютерная конференция IRE-AIEE-ACM. IRE-AIEE-ACM '59 (Восточный): 133–138. Дои:10.1145/1460299.1460314.
- ^ Лоури, Эдвард С .; Медлок, Клеберн В. (январь 1969 г.). «Оптимизация объектного кода». Коммуникации ACM. 12 (1): 13–22. Дои:10.1145/362835.362838.
- ^ Ситрон, Рон; Ферранте, Жанна; Розен, Барри К .; Wegman, Mark N .; Задек, Ф. Кеннет (1989). «Эффективный метод вычисления статической формы единственного присвоения». Материалы 16-го симпозиума ACM SIGPLAN-SIGACT по принципам языков программирования. ПОПЛ ’89: 25–35. Дои:10.1145/75277.75280. ISBN 0897912942.
- ^ "Доминатор Дерево". eclipse.org. SAP AG и IBM Corporation. 2012 [2008]. Получено 21 июн 2013.
- ^ Тесленко, Максим; Дуброва, Елена (2005). Эффективный алгоритм поиска двухвершинных доминаторов в схемных графах. Труды конференции по проектированию и испытаниям в Европе. Дата '05. С. 406–411. CiteSeerX 10.1.1.598.3053. Дои:10.1109 / ДАТА.2005.53. ISBN 9780769522883.
- ^ Дуброва, Елена (2005). Структурное тестирование на основе минимального количества ядер. Труды конференции по проектированию и испытаниям в Европе. Дата '05. С. 1168–1173. CiteSeerX 10.1.1.583.5547. Дои:10.1109 / ДАТА.2005.284. ISBN 9780769522883.
- ^ Георгиадис, Лукас; Тарджан, Роберт Э.; Вернек, Ренато Ф. (2006). «Поиск доминаторов на практике» (PDF).
- ^ Купер, Кейт Д.; Харви, Тимоти Дж; Кеннеди, Кен (2001). «Простой и быстрый алгоритм доминирования» (PDF).