WikiDer > Разложение динамического режима
Эта статья поднимает множество проблем. Пожалуйста помоги Улучши это или обсудите эти вопросы на страница обсуждения. (Узнайте, как и когда удалить эти сообщения-шаблоны) (Узнайте, как и когда удалить этот шаблон сообщения)
|
Разложение динамического режима (DMD) это уменьшение размерности алгоритм, разработанный Питером Шмидом в 2008 году. Получив временные ряды данных, DMD вычисляет набор режимов, каждый из которых связан с фиксированной частотой колебаний и скоростью затухания / роста. В частности, для линейных систем эти режимы и частоты аналогичны нормальные режимы системы, но в более общем плане они являются приближениями мод и собственных значений оператор композиции (также называется оператором Купмана). Из-за внутреннего временного поведения, связанного с каждым режимом, DMD отличается от таких методов уменьшения размерности, как Анализ главных компонентов, который вычисляет ортогональные режимы, в которых отсутствует заранее определенное временное поведение. Поскольку его режимы не ортогональны, представления на основе DMD могут быть менее экономичными, чем те, которые генерируются PCA. Однако они также могут быть более значимыми с физической точки зрения, поскольку каждый режим связан с затухающим (или управляемым) синусоидальным поведением во времени.
Обзор
Разложение динамических мод было впервые введено Шмидом как численная процедура для извлечения динамических характеристик из данных потока.[1]
Данные имеют форму последовательности снимков.
где это -й снимок поля потока, и представляет собой матрицу данных, столбцы которой являются отдельными снимками. Нижний и верхний индекс обозначают индекс снимка в первом и последнем столбцах соответственно. Предполагается, что эти снимки связаны линейным отображением, которое определяет линейная динамическая система
это остается примерно таким же в течение периода выборки. Написанное в матричной форме, это означает, что
где вектор остатков, который учитывает поведение, которое не может быть полностью описано с помощью , , , и . Независимо от подхода, выходом DMD являются собственные значения и собственные векторы , которые называются Собственные значения DMD и Режимы DMD соответственно.
Алгоритм
Есть два метода получения этих собственных значений и мод. Первый Подобный Арнольди, который полезен для теоретического анализа из-за его связи с Крылова методы. Второй - это разложение по сингулярным числам (SVD) подход, более устойчивый к шумам в данных и числовым ошибкам.
Подход Арнольди
В приложениях с жидкостями размер снимка, , предполагается, что намного больше, чем количество снимков , поэтому есть много равнозначных вариантов . Исходный алгоритм DMD выбирает так что каждый из снимков в можно записать как линейную комбинацию снимков в Поскольку большинство снимков появляется в обоих наборах данных, это представление не содержит ошибок для всех снимков, кроме , который записывается как
где представляет собой набор коэффициентов, которые DMD должен идентифицировать и - остаток.
где это сопутствующая матрица
Вектор может быть вычислен путем решения задачи наименьших квадратов, которая минимизирует общую невязку. В частности, если мы возьмем QR-разложение , тогда .
В этой форме МДД является разновидностью Метод Арнольди, а значит, и собственные значения являются приближениями собственных значений . Кроме того, если является собственным вектором , тогда является приближенным собственным вектором . Причина собственное разложение выполняется на скорее, чем это потому что намного меньше, чем , поэтому вычислительная стоимость DMD определяется количеством снимков, а не размером снимка.
Подход на основе СВД
Вместо вычисления сопутствующей матрицы , подход на основе SVD дает матрицу это связано с через преобразование подобия. Для этого предположим, что у нас есть СВД . потом
Эквивалентно предположению, сделанному в рамках подхода, основанного на Арнольди, мы выбираем так что снимки в можно записать как линейную суперпозицию столбцов в , что эквивалентно требованию, чтобы их можно было записать как суперпозицию Режимы POD. С этим ограничением минимизация остатка требует, чтобы он был ортогонален базису POD (т.е. ). Затем умножая обе части приведенного выше уравнения на дает , которыми можно манипулировать, чтобы получить
Потому что и связаны преобразованием подобия, собственные значения являются собственными значениями , и если является собственным вектором , тогда является собственным вектором .
Таким образом, подход на основе SVD выглядит следующим образом:
- Разделите временной ряд данных на в две матрицы и .
- Вычислить SVD .
- Сформировать матрицу , и вычислить его собственные значения и собственные векторы .
- В -ое собственное значение DMD равно и -й режим DMD - это .
Преимущество подхода на основе SVD перед подходом, подобным подходу Арнольди, заключается в том, что шум в данных и проблемы численного усечения могут быть компенсированы усечением SVD . Как отмечено в [1] без этого шага усечения может оказаться затруднительным точное вычисление большего количества мод и собственных значений, чем первая пара, на экспериментальных наборах данных.
Теоретические и алгоритмические достижения
С момента его создания в 2010 году значительный объем работы был сосредоточен на понимании и улучшении МДД. Один из первых анализов МДД, выполненный Rowley et al.[2] установил связь между DMD и оператором Купмана и помог объяснить выходные данные DMD в применении к нелинейным системам. С тех пор был разработан ряд модификаций, которые либо усиливают эту связь, либо повышают надежность и применимость подхода.
- Оптимизированный DMD: Оптимизированный DMD - это модификация исходного алгоритма DMD, разработанная для компенсации двух ограничений этого подхода: (i) сложность выбора режима DMD и (ii) чувствительность DMD к шуму или другим ошибкам на последнем снимке Временные ряды.[3] Оптимизированный DMD преобразовывает процедуру DMD в задачу оптимизации, в которой идентифицированный линейный оператор имеет фиксированный ранг. Кроме того, в отличие от DMD, который идеально воспроизводит все снимки, кроме последнего, Optimized DMD позволяет распределять ошибки реконструкции по набору данных, что, по-видимому, делает подход более надежным на практике.
- Оптимальное разложение по модам: Оптимальное разложение по режимам (OMD) преобразовывает процедуру DMD в задачу оптимизации и позволяет пользователю напрямую определять ранг идентифицированной системы.[4] При правильном выборе этого ранга OMD может создавать линейные модели с меньшими остаточными ошибками и более точными собственными значениями как на синтетических, так и на экспериментальных наборах данных.
- Точный МДД: Алгоритм Exact DMD обобщает исходный алгоритм DMD двумя способами. Во-первых, в исходном алгоритме DMD данные должны быть временными рядами снимков, но Exact DMD принимает набор данных пар снимков.[5] Снимки в паре должны быть разделены фиксированным , но необязательно извлекать из одного временного ряда. В частности, Exact DMD позволяет объединить данные нескольких экспериментов в единый набор данных. Во-вторых, оригинальный алгоритм DMD эффективно предварительно обрабатывает данные, проецируя их на набор режимов POD. Алгоритм Exact DMD удаляет этот этап предварительной обработки и может создавать режимы DMD, которые нельзя записать как суперпозицию режимов POD.
- Распространенность МДД: DMD, способствующий разреженности, представляет собой процедуру постобработки для режима DMD и выбора собственных значений.[6] МДД, способствующий редкости, использует штраф для определения меньшего набора важных режимов DMD и является альтернативным подходом к проблеме выбора режима DMD, который можно эффективно решить с помощью методы выпуклой оптимизации.
- МДД с несколькими разрешениями: DMD с несколькими разрешениями (mrDMD) - это комбинация методов, используемых в анализ с несколькими разрешениями с Exact DMD, предназначенным для надежного извлечения режимов DMD и собственных значений из наборов данных, содержащих несколько временных шкал.[7] Подход mrDMD был применен к данным о глобальной температуре поверхности и определяет режим DMD, который появляется в годы Эль-Ниньо.
- Расширенный МДД: Extended DMD - это модификация Exact DMD, которая усиливает связь между DMD и оператором Купмана.[8] Как следует из названия, Extended DMD - это расширение DMD, которое использует более богатый набор наблюдаемых функций для получения более точных приближений оператора Купмана. Он также продемонстрировал, что DMD и связанные с ним методы позволяют получить приближения собственных функций Купмана в дополнение к более часто используемым собственным значениям и модам.
- DMD с контролем: Разложение динамического режима с контролем (DMDc) [9] представляет собой модификацию процедуры DMD, предназначенную для данных, полученных от систем ввода-вывода. Одной из уникальных особенностей DMDc является способность устранять неоднозначность эффектов срабатывания системы от динамики разомкнутого контура, что полезно, когда данные получены при наличии срабатывания.
- Всего наименьших квадратов DMD: Total Least Squares DMD - это недавняя модификация Exact DMD, предназначенная для решения проблем устойчивости к шумам измерения в данных. В,[10] авторы интерпретируют Exact DMD как проблему регрессии, которая решается с использованием обыкновенный метод наименьших квадратов (OLS), который предполагает отсутствие шума в регрессорах. Это предположение создает смещение в собственных значениях DMD, когда оно применяется к наборам экспериментальных данных, где все наблюдения зашумлены. Метод наименьших квадратов DMD заменяет задачу OLS на общая задача наименьших квадратов, что устраняет эту предвзятость.
- Разложение динамического распределения: DDD фокусируется на прямой задаче в непрерывном времени, т.е. оператор передачи. Однако разработанный метод можно также использовать для решения задач DMD в непрерывном режиме.[11]
В дополнение к алгоритмам, перечисленным здесь, были разработаны аналогичные методы для конкретных приложений. Например, как DMD, Метод Прони представляет сигнал как суперпозицию затухающие синусоиды. В науке о климате линейное обратное моделирование также тесно связано с DMD.[12] Для более полного списка см. Tu et al.[5]
Примеры
Эта секция возможно содержит оригинальные исследования. (Март 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Задняя кромка профиля
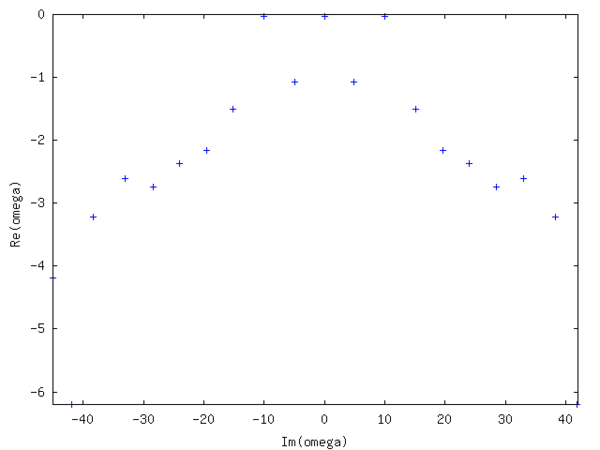
След за препятствием в потоке может вызвать Карман вихревая улица. На рис.1 показано слияние вихря за задней кромкой профиля. DMD-анализ был применен к 90 последовательным полям энтропии. (анимированный gif (1,9 МБ))и получить приближенный спектр собственных значений, как показано ниже. Анализ был применен к численным результатам без обращения к основным уравнениям. Профиль отображается белым цветом. Белые дуги - это границы процессора, поскольку вычисление выполнялось на параллельном компьютере с использованием разных вычислительных блоков.
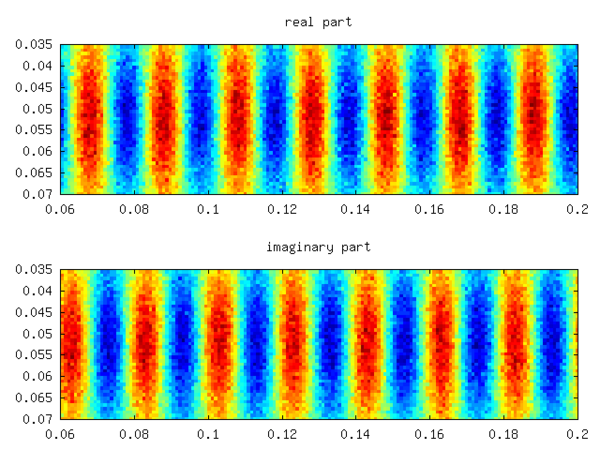
Примерно треть спектра была сильно затухающей (большой, отрицательный ) и не показан. Доминирующий режим линьки показан на следующих рисунках. Изображение слева - действительная часть, изображение справа - мнимая часть собственного вектора.
 |  |
Опять же, на этом рисунке показан собственный вектор энтропии. Акустическое содержание той же моды видно в нижней половине следующего графика. Верхняя половина соответствует энтропийному режиму, как указано выше.
Синтетический пример схемы передвижения
Анализ DMD предполагает образец формыгде - любая из независимых переменных задачи, но ее нужно выбрать заранее. Возьмем, например, шаблон
Со временем в качестве предварительно выбранного экспоненциального множителя.
На следующем рисунке показан образец с , и . Левое изображение показывает образец без, правое с добавлением шума. Амплитуда случайного шума такая же, как у шаблона.
Анализ DMD выполняется с 21 искусственно созданным полем с использованием временного интервала , ограничивая анализ .
Спектр симметричный и показывает три практически незатухающие моды (небольшая отрицательная действительная часть), тогда как остальные моды сильно затухают. Их числовые значения равны соответственно. Реальный соответствует среднему значению поля, тогда как соответствует наложенному шаблону с . Относительная ошибка -1/1000. Увеличение шума до 10-кратного значения сигнала дает примерно такую же ошибку. Действительная и мнимая части одной из последних двух собственных мод изображены на следующем рисунке.
Смотрите также
Существует несколько других декомпозиций экспериментальных данных. Если основные уравнения доступны, разложение по собственным значениям может быть возможным.
- Разложение на собственные значения
- Разложение по эмпирическим модам
- Глобальный режим
- Нормальный режим
- Правильное ортогональное разложение
- Разложение по сингулярным числам
Рекомендации
- ^ а б П.Дж. Шмид. «Динамическая модовая декомпозиция численных и экспериментальных данных». Журнал гидромеханики 656.1 (2010): 5–28.
- ^ К. В. Роули, И. Мезич, С. Багери, П. Шлаттер и Д. С. Хеннингсон, "Спектральный анализ нелинейных потоков". Журнал гидромеханики 641 (2009): 85-113
- ^ К.К. Чен, Дж. Ту, и К.В. Роули, "Варианты разложения динамического режима: граничные условия, Купман и анализ Фурье". Журнал нелинейной науки 22 (2012): 887-915.
- ^ А. Винн, Д. С. Пирсон, Б. Ганапатисубрамани и П. Дж. Гуларт, "Оптимальное разложение мод для нестационарных потоков". Журнал гидромеханики 733 (2013): 473-503
- ^ а б Ту, Роули, Лучтенбург, Брантон и Куц (декабрь 2014 г.). «О динамической модовой декомпозиции: теория и приложения». Американский институт математических наук. arXiv:1312.0041. Дои:10.3934 / jcd.2014.1.391.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ М.Р. Йованович, П.Дж. Шмид, Дж. У. Николс, "Разложение динамических мод, способствующих разреженности". Физика жидкостей 26 (2014)
- ^ J.N. Куц, Х. Фу и С.Л. Брантон, "Разложение динамических мод с несколькими разрешениями". Препринт arXiv arXiv: 1506.00564 (2015).
- ^ М.О. Уильямс, И. Кеврекидис, К.В. Роули, "Управляемая данными приближения оператора Купмана: расширение динамического разложения мод". Журнал нелинейной науки 25 (2015): 1307-1346.
- ^ J.L. Proctor, S.L. Брантон, Дж. Куц, «Разложение динамического режима с контролем». Препринт arXiv arXiv: 1409.6358 (2014).
- ^ РС. Hemati, C.W. Rowley, E.A. Дим, Л. Каттафеста, "Снятие смещения динамической разложения мод для прикладного спектрального анализа Купмана зашумленных наборов данных". Препринт arXiv arXiv: 1502.03854 (2015).
- ^ Тейлор-Кинг, Джейк П .; Riseth, Asbjørn N .; Макнейр, Уилл; Клаассен, Манфред (10.01.2020). «Разложение динамического распределения для временных рядов моментальных снимков одной ячейки определяет субпопуляции и траектории во время перепрограммирования ИПСК». PLOS вычислительная биология. 16 (1): e1007491. Дои:10.1371 / journal.pcbi.1007491. ISSN 1553-7358. ЧВК 6953770. PMID 31923173.
- ^ Пенланд, Магориан, Сесиль, Тереза (1993). «Прогноз температуры поверхности моря Niño 3 с использованием линейного обратного моделирования». J. Климат. 6.
- Шмид, П. Дж. И Сестерхенн, Дж. Л. 2008. Разложение численных и экспериментальных данных в динамическом режиме. В Bull. Амер. Phys. Soc., 61-е заседание APS, стр. 208. Сан-Антонио.
- Хассельманн, К., 1988. СОЗ и ГПИ. Редукция сложных динамических систем с использованием основных моделей колебаний и взаимодействия. J. Geophys. Res., 93 (D9): 10975–10988.