WikiDer > Сужение края

Стягивая ребро между указанными вершинами, получаем граф G / {uv}.

В теория графов, сжатие края является операция который удаляет ребро из графа, одновременно объединяя две вершины, которые он ранее соединял. Стягивание краев - фундаментальная операция в теории граф миноры. Идентификация вершины это менее ограничительная форма этой операции.

Определение

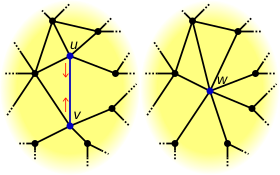
В сжатие края операция происходит относительно определенного ребра, ${displaystyle e}$. Край ${displaystyle e}$ удаляется и две его инцидентные вершины, ${displaystyle u}$ и ${displaystyle v}$, объединяются в новую вершину ${displaystyle w}$, где ребра, инцидентные ${displaystyle w}$ каждый соответствует ребру, инцидентному либо ${displaystyle u}$ или же ${displaystyle v}$. В более общем смысле, операция может быть выполнена для набора ребер путем сжатия каждого ребра (в любом порядке).^[1]

Полученный индуцированный граф иногда записывают как ${displaystyle G / e}$. (Сравните это с ${displaystyle Gsetminus e}$ что означает удаление края ${displaystyle e}$.)

Сужение кромки без создания нескольких кромок.

Как определено ниже, операция стягивания ребер может привести к графу с несколько краев даже если исходный график был простой график.^[2] Однако некоторые авторы^[3] запретить создание нескольких ребер, чтобы сокращения ребер, выполняемые на простых графах, всегда давали простые графы.

Формальное определение

Позволять ${displaystyle G = (V, E)}$ быть графом (или же ориентированный граф) содержащий ребро ${displaystyle e = (u, v)}$ с ${displaystyle ueq v}$. Позволять ${displaystyle f}$ - функция, отображающая каждую вершину в ${displaystyle Vsetminus {u, v}}$ в себя, а в противном случае отображает его в новую вершину ${displaystyle w}$.Сокращение ${displaystyle e}$ приводит к новому графику ${displaystyle G '= (V', E ')}$, куда ${displaystyle V '= (Vsetminus {u, v}) чашка {w}}$, ${displaystyle E '= Esetminus {e}}$, и для каждого ${displaystyle xin V}$, ${displaystyle x '= F (x) in V'}$ падает на край ${displaystyle e'in E '}$ тогда и только тогда, когда соответствующее ребро, ${displaystyle ein E}$ имеет отношение к ${displaystyle x}$ в ${displaystyle G}$.

Идентификация вершины

Идентификация вершины (иногда называют сокращение вершины) снимает ограничение, что сокращение должно происходить над вершинами, разделяющими инцидентное ребро. (Таким образом, стягивание ребер является частным случаем идентификации вершин.) Операция может выполняться с любой парой (или подмножеством) вершин в графе. Края между двумя договор вершины иногда удаляются. Если ${displaystyle v}$ и ${displaystyle v '}$ являются вершинами различных компонент ${displaystyle G}$, тогда мы можем создать новый график ${displaystyle G '}$ путем выявления ${displaystyle v}$ и ${displaystyle v '}$ в ${displaystyle G}$ как новая вершина ${displaystyle {extbf {v}}}$ в ${displaystyle G '}$.^[4] В более общем плане, учитывая раздел множества вершин можно идентифицировать вершины в разбиении; получившийся граф известен как факторный граф.

Скалывание вершин

Скалывание вершин что то же самое, что и разбиение вершин, означает, что одна вершина разбивается на две, где эти две новые вершины смежны с вершинами, с которыми была смежна исходная вершина. Это операция, обратная идентификации вершины.

Сужение пути

Сужение пути происходит на множестве ребер в дорожка который договор чтобы образовать единую кромку между конечными точками пути. Ребра, инцидентные вершинам на пути, либо удаляются, либо произвольно (или систематически) соединяются с одной из конечных точек.

Скручивание

Даны два непересекающихся графа ${displaystyle G_ {1}}$ и ${displaystyle G_ {2}}$, куда ${displaystyle G_ {1}}$ содержит вершины ${displaystyle u_ {1}}$ и ${displaystyle v_ {1}}$ и ${displaystyle G_ {2}}$ содержит вершины ${displaystyle u_ {2}}$ и ${displaystyle v_ {2}}$. Предположим, мы можем получить график ${displaystyle G}$ путем определения вершин ${displaystyle u_ {1}}$ из ${displaystyle G_ {1}}$ и ${displaystyle u_ {2}}$ из ${displaystyle G_ {2}}$ как вершина ${displaystyle u}$ из ${displaystyle G}$ и определение вершин ${displaystyle v_ {1}}$ из ${displaystyle G_ {1}}$ и ${displaystyle v_ {2}}$ из ${displaystyle G_ {2}}$ как вершина ${displaystyle v}$ из ${displaystyle G}$. В скручивание ${displaystyle G '}$ из ${displaystyle G}$ относительно множества вершин ${displaystyle {u, v}}$, вместо этого мы определяем ${displaystyle u_ {1}}$ с ${displaystyle v_ {2}}$ и ${displaystyle v_ {1}}$ с ${displaystyle u_ {2}}$.^[5]

Приложения

Методы сжатия ребер и вершин ценны в Доказательство по индукции от числа вершин или ребер в графе, где можно предположить, что свойство выполняется для всех меньших графов, и это можно использовать для доказательства свойства для большего графа.

Сужение ребер используется в рекурсивной формуле для количества остовных деревьев произвольного связного графа,^[6] и в рекуррентной формуле для хроматический полином простого графа.^[7]

Сокращения также полезны в структурах, где мы хотим упростить граф, идентифицируя вершины, которые представляют по существу эквивалентные объекты. Один из наиболее распространенных примеров - сокращение общего ориентированный граф для ациклический ориентированный граф сжав все вершины в каждом компонент сильной связности. Если отношение, описываемое графиком, имеет вид переходный, никакая информация не теряется, пока мы помечаем каждую вершину набором меток вершин, которые были сжаты для ее образования.

Другой пример - объединение, выполненное в распределение регистров раскраски глобального графа, где вершины сужаются (где это безопасно), чтобы исключить операции перемещения между отдельными переменными.

Сужение кромок используется в пакетах 3D-моделирования (вручную или с помощью некоторых функций программного обеспечения для моделирования) для последовательного уменьшения количества вершин, помогая создавать низкополигональные модели.

Смотрите также

• Подразделение (теория графов)

Примечания

Рекомендации

• Гросс, Джонатан; Йеллен, Джей (1998), Теория графов и ее приложения, CRC Press, ISBN 0-8493-3982-0
• Оксли, Джеймс (1992), Матроид Теория, Oxford University Press
• Розен, Кеннет (2011), Дискретная математика и ее приложения (7-е изд.), Макгроу-Хилл, ISBN 9780073383095
• Запад, Дуглас Б. (2001), Введение в теорию графов (2-е изд.), Прентис-Холл, ISBN 0-13-014400-2

внешняя ссылка

• Вайсштейн, Эрик В. «Сжатие края». MathWorld.