WikiDer > Восьмиточный алгоритм
В восьмиточечный алгоритм алгоритм, используемый в компьютерное зрение оценить основная матрица или фундаментальная матрица относящийся к паре стереокамер из набора соответствующих точек изображения. Он был представлен Кристофер Лонге-Хиггинс в 1981 г. для случая существенной матрицы. Теоретически этот алгоритм можно использовать и для фундаментальной матрицы, но на практике нормализованный восьмибалльный алгоритм, описанный Ричардом Хартли в 1997 году, лучше подходит для этого случая.
Название алгоритма происходит от того факта, что он оценивает существенную матрицу или фундаментальную матрицу по набору из восьми (или более) соответствующих точек изображения. Однако варианты алгоритма можно использовать менее чем для восьми точек.
Ограничение компланарности
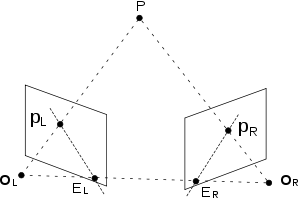
Можно выразить эпиполярная геометрия двух камер и точки в пространстве с алгебраическим уравнением. Обратите внимание, где бы ни находилась точка находится в пространстве, векторы , и принадлежат к одной плоскости. Вызов координаты точки в системе отсчета левого глаза и вызовите координаты в системе отсчета правого глаза и вызовите вращение и перевод между двумя системами отсчета s.t. это связь между координатами в двух системах отсчета. Следующее уравнение всегда выполняется, потому что вектор, созданный из ортогонален обоим и :
Потому что , мы получили
- .
Замена с , мы получили
Заметьте, что можно рассматривать как матрицу; Лонге-Хиггинс использовал символ чтобы обозначить это. Продукт часто называют основная матрица и обозначен .
Векторы параллельны векторам и поэтому ограничение компланарности выполняется, если мы подставляем эти векторы. Если мы позвоним координаты проекций на левую и правую плоскости изображения, то ограничение компланарности может быть записано как
Базовый алгоритм
Здесь описан базовый восьмибалльный алгоритм для случая оценки существенной матрицы . Он состоит из трех шагов. Во-первых, он формулирует однородное линейное уравнение, где решение напрямую связано с , а затем решает уравнение, учитывая, что оно может не иметь точного решения. Наконец, управляются внутренние ограничения результирующей матрицы. Первый шаг описан в статье Лонге-Хиггинса, второй и третий шаги представляют собой стандартные подходы в теории оценивания.
Ограничение, определяемое существенной матрицей является
для соответствующих точек изображения, представленных в нормализованных координатах изображения . Задача, которую решает алгоритм, - определить для набора совпадающих точек изображения. На практике координаты изображений точек изображения подвержены влиянию шума, и решение также может быть переопределено, что означает, что может быть невозможно найти которое удовлетворяет указанному выше ограничению точно для всех точек. Эта проблема решается на втором этапе алгоритма.
Шаг 1. Формулировка однородное линейное уравнение
С
- и и
ограничение также можно переписать как
или же
куда
- и
то есть, представляет собой существенную матрицу в виде 9-мерного вектора, и этот вектор должен быть ортогонален вектору которое можно рассматривать как векторное представление матрица .
Каждая пара соответствующих точек изображения дает вектор . Учитывая набор 3D-точек это соответствует набору векторов и все они должны удовлетворить
для вектора . Для достаточно большого числа (не менее восьми) линейно независимых векторов можно определить простым способом. Собрать все векторы как столбцы матрицы и тогда должно быть так, что
Это означает, что это решение однородное линейное уравнение.
Шаг 2: решение уравнения
Стандартный подход к решению этого уравнения подразумевает, что это левый сингулярный вектор из соответствующий исключительное значение что равно нулю. При условии, что не менее восьми линейно независимых векторов используются для построения отсюда следует, что этот сингулярный вектор единственен (без учета скалярного умножения) и, следовательно, а потом можно определить.
В случае использования более восьми соответствующих точек для построения возможно, что у него нет сингулярного значения, равного нулю. На практике такой случай имеет место, когда на координаты изображения влияют различные типы шума. Обычный подход к этой ситуации - описать ее как Всего наименьших квадратов проблема; найти что сводит к минимуму
когда . Решение - выбрать как левый сингулярный вектор, соответствующий самый маленький исключительное значение . Переупорядочивание этого обратно в матрица дает результат этого шага, называемого здесь .
Шаг 3. Обеспечение внутреннего ограничения
Другим следствием работы с координатами зашумленного изображения является то, что результирующая матрица может не удовлетворять внутреннему ограничению основной матрицы, то есть два из ее сингулярных значений равны и не равны нулю, а другое - нулю. В зависимости от приложения, меньшие или большие отклонения от внутреннего ограничения могут быть или не быть проблемой. Если критически важно, чтобы оцениваемая матрица удовлетворяла внутренним ограничениям, это можно сделать, найдя матрицу ранга 2, что минимизирует
куда матрица, полученная на шаге 2, а Норма матрицы Фробениуса используется. Решение проблемы дается сначала вычислением разложение по сингулярным числам из :
куда ортогональные матрицы и - диагональная матрица, содержащая сингулярные значения . В идеальном случае один из диагональных элементов должен быть нулевым или хотя бы маленьким по сравнению с двумя другими, которые должны быть равны. В любом случае установите
куда - наибольшее и второе наибольшее сингулярные значения в соответственно. Ну наконец то, дан кем-то
Матрица - итоговая оценка существенной матрицы, предоставляемой алгоритмом.
Нормализованный алгоритм
Базовый восьмиточечный алгоритм в принципе можно использовать также для оценки фундаментальной матрицы . Определяющее ограничение для является
куда являются однородными представлениями соответствующих координат изображения (не обязательно нормализованными). Это означает, что можно сформировать матрицу аналогично основной матрице и решить уравнение
за который является измененной версией . Следуя описанной выше процедуре, можно определить из набора из восьми совпадающих точек. Однако на практике полученная фундаментальная матрица может оказаться бесполезной для определения эпиполярных ограничений.
Сложность
Проблема в том, что в результате часто бывает плохо воспитанный. В теории, должно иметь одно сингулярное значение, равное нулю, а остальные ненулевые. Однако на практике некоторые из ненулевых сингулярных значений могут стать маленькими по сравнению с большими. Если более восьми соответствующих точек используются для построения , где координаты являются приблизительно правильными, может не быть четко определенного сингулярного значения, которое можно определить как приблизительно ноль. Следовательно, решение однородной линейной системы уравнений может быть недостаточно точным, чтобы быть полезным.
Причина
Хартли обратился к этой проблеме оценки в своей статье 1997 года. Его анализ проблемы показывает, что проблема вызвана плохим распределением координат однородных изображений в их пространстве, . Типичное однородное представление координат 2D-изображения является
где оба лежат в диапазоне от 0 до 1000–2000 для современной цифровой камеры. Это означает, что первые две координаты в изменяются в гораздо большем диапазоне, чем третья координата. Кроме того, если точки изображения, которые используются для построения лежат в относительно небольшой области изображения, например на , снова вектор указывает более или менее в одном направлении для всех точек. Как следствие, будет иметь одно большое сингулярное значение, а остальные - маленькие.
Решение
В качестве решения этой проблемы Хартли предложил преобразовать систему координат каждого из двух изображений независимо в новую систему координат в соответствии со следующим принципом.
- Начало новой системы координат должно быть отцентрировано (иметь начало) в центроиде (центре тяжести) точек изображения. Это достигается путем перевода исходного источника в новый.
- После переноса координаты равномерно масштабируются, так что среднее расстояние от начала координат до точки равно .
Этот принцип обычно приводит к отдельному преобразованию координат для каждого из двух изображений. В результате новые однородные координаты изображения даны
куда трансформации (перевод и масштабирование) от старого к новому нормализованные координаты изображения. Эта нормализация зависит только от точек изображения, которые используются в одном изображении, и, как правило, отличается от нормализованных координат изображения, созданных нормализованной камерой.
Эпиполярное ограничение, основанное на фундаментальной матрице, теперь можно переписать как
куда . Это означает, что можно использовать нормализованные координаты однородного изображения. оценить преобразованную фундаментальную матрицу используя базовый восьмибалльный алгоритм, описанный выше.
Цель преобразований нормализации состоит в том, чтобы матрица , построенный из нормализованных координат изображения, в общем случае имеет лучшее число обусловленности, чем имеет. Это означает, что решение более точно определяется как решение однородного уравнения чем относительно . Один раз был определен и преобразован в последний может быть денормализованный давать в соответствии с
В общем, эта оценка фундаментальной матрицы лучше, чем была бы получена путем оценки по ненормированным координатам.
Использование менее восьми точек
Каждая пара точек вносит свой вклад с одним ограничивающим уравнением для элемента в . С имеет пять степеней свободы, поэтому достаточно всего пяти пар точек для определения . Хотя это возможно с теоретической точки зрения, практическая реализация этого не является простой и зависит от решения различных нелинейных уравнений.
Каве Фатиан и др. предложены алгоритмы для пяти, шести и семи точек, которые обходят вычисление существенной матрицы, вычисляя кватернион вращения напрямую.[1][2]
Смотрите также
Рекомендации
- ^ Фатиан, Кавех (2018). «QuEst: подход на основе кватернионов для оценки движения камеры по минимальным характерным точкам». Письма IEEE по робототехнике и автоматизации. arXiv:1704.02672. Дои:10.1109 / LRA.2018.2792142.
- ^ Фатиан, Кавех (2018). «Оценка относительной позы камеры для визуального следящего с использованием кватернионов». Робототехника и автономные системы. Дои:10.1016 / j.robot.2018.05.014.
дальнейшее чтение
- Ричард И. Хартли (июнь 1997 г.). «В защиту восьмибалльного алгоритма». IEEE Transactions по распознаванию образов и машинному анализу. 19 (6): 580–593. Дои:10.1109/34.601246.
- Ричард Хартли и Эндрю Зиссерман (2003). Многоканальная геометрия в компьютерном зрении. Издательство Кембриджского университета. ISBN 978-0-521-54051-3.
- Х. Кристофер Лонге-Хиггинс (сентябрь 1981 г.). «Компьютерный алгоритм восстановления сцены из двух проекций». Природа. 293 (5828): 133–135. Дои:10.1038 / 293133a0.