WikiDer > Соотношение Фабера – Джексона

Дисперсия скорости (у-axis) нанесен на абсолютная величина (Икс-ось) для образца эллиптические галактики, причем соотношение Фабера – Джексона показано синим цветом.

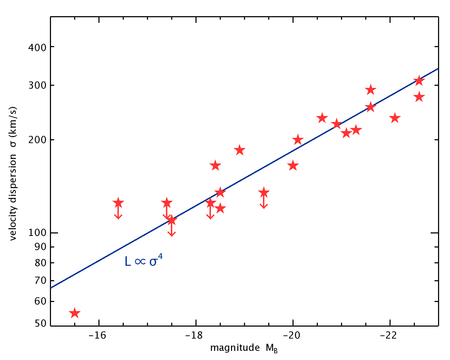
В Соотношение Фабера – Джексона предоставил первый эмпирический сила закона отношения между яркость ${displaystyle L}$ и центральный звездный дисперсия скоростей ${displaystyle sigma}$ из эллиптическая галактика, и был представлен астрономами Сандра М. Фабер и Роберт Эрл Джексон в 1976 году. Их отношение можно выразить математически следующим образом:

${displaystyle Lpropto sigma ^ {gamma}}$

с индексом ${displaystyle gamma}$ примерно равно 4.

В 1962 г. Рудольф Минковски открыл и написал, что «корреляция между дисперсией скоростей и [светимостью] существует, но она плохая» и что «кажется важным расширить наблюдения на большее количество объектов, особенно при низких и средних абсолютных величинах».^[1] Это было важно, потому что ценность ${displaystyle gamma}$ зависит от диапазона яркости галактик, который соответствует, со значением 2 для эллиптических галактик с низкой светимостью, обнаруженных группой во главе с Роджер Дэвис,^[2] и значение 5 сообщается Пол Л. Шехтер для светящихся эллиптических галактик.^[3]

Соотношение Фабера – Джексона понимается как проекция Фундаментальный план эллиптических галактик. Одно из основных его применений - это инструмент для определения расстояний до внешних галактик.

Теория

В гравитационный потенциал распределения масс радиуса ${displaystyle R}$ и масса ${displaystyle M}$ дается выражением:

${displaystyle U = -alpha {frac {GM ^ {2}} {R}}}$

Где α - константа, зависящая, например, на профиле плотности системы, а G - гравитационная постоянная. Для постоянной плотности ${displaystyle alpha = {frac {3} {5}}}$

Кинетическая энергия равна:

${displaystyle K = {frac {1} {2}} MV ^ {2} = {frac {3} {2}} Msigma ^ {2}}$

(Отзывать ${displaystyle sigma}$ - одномерная дисперсия скорости. Следовательно, ${displaystyle 3sigma ^ {2} = V ^ {2}}$.) От теорема вириала (${displaystyle 2K + U = 0}$ ) следует

${displaystyle sigma ^ {2} = {frac {1} {5}} {frac {GM} {R}}.}$

Если предположить, что отношение массы к свету, ${displaystyle M / L}$, является постоянным, например ${displaystyle Mpropto L}$ мы можем использовать это и вышеприведенное выражение, чтобы получить связь между ${displaystyle R}$ и ${displaystyle sigma ^ {2}}$:

${displaystyle Rpropto {frac {LG} {sigma ^ {2}}}.}$

Введем поверхностную яркость, ${displaystyle B = L / (4pi R ^ {2})}$ и предположим, что это константа (что с фундаментальной теоретической точки зрения является совершенно неоправданным предположением), чтобы получить

${displaystyle L = 4pi R ^ {2} B.}$

Используя это и комбинируя его с отношением между ${displaystyle R}$ и ${displaystyle L}$, это приводит к

${displaystyle Lpropto 4pi left ({frac {LG} {sigma ^ {2}}} ight) ^ {2} B}$

и, переписав приведенное выше выражение, мы окончательно получим связь между светимостью и дисперсией скоростей:

${displaystyle Lpropto {frac {sigma ^ {4}} {4pi G ^ {2} B}},}$

то есть

${displaystyle Lpropto sigma ^ {4}.}$

Учитывая, что массивные галактики возникают в результате гомологического слияния, а более слабые - в результате диссипации, предположение о постоянной поверхностной яркости больше не может поддерживаться. Эмпирически поверхностная яркость показывает пик примерно при ${displaystyle M_ {V} = - 23}$. Исправленное отношение затем становится

${displaystyle Lpropto sigma ^ {3.1}}$

для менее массивных галактик и

${displaystyle Lpropto sigma ^ {15.0}}$

для более массивных. С помощью этих измененных формул основная плоскость разделяется на две плоскости, наклоненные друг к другу примерно на 11 градусов.

Даже скопления галактик первого ранга не имеют постоянной поверхностной яркости. Заявление о постоянной яркости поверхности было представлено астрономом. Аллан Р. Сэндидж в 1972 г. на основе трех логических аргументов и собственных эмпирических данных. В 1975 г. Дональд Гудехус показали, что каждый из логических аргументов неверен и что галактики скопления, занявшие первое место, демонстрируют стандартное отклонение около половины звездной величины.

Оценка расстояний до галактик

Подобно соотношению Талли – Фишера, соотношение Фабера – Джексона позволяет оценить расстояние до галактики, которое иначе трудно получить, связав его с более легко наблюдаемыми свойствами галактики. В случае эллиптических галактик, если можно измерить центральную дисперсию звездных скоростей, что относительно легко сделать, используя спектроскопия измерить Доплеровский сдвиг света, излучаемого звездами, то можно получить оценку истинной светимости галактики с помощью соотношения Фабера – Джексона. Это можно сравнить с кажущаяся величина галактики, что дает оценку модуль расстояния и, следовательно, расстояние до галактики.

Комбинируя дисперсию центральной скорости галактики с измерениями ее центральной поверхностной яркости и параметра радиуса, можно еще больше улучшить оценку расстояния до галактики. Этот стандартный критерий, или «приведенный параметр-радиус галактики», ${displaystyle r_ {g}}$, разработанный Гудехусом в 1991 году, может давать расстояния без систематической ошибки с точностью до 31%.

Смотрите также

• Фундаментальная плоскость (эллиптические галактики)
• Соотношение Талли – Фишера
• M-сигма отношение

Рекомендации

внешняя ссылка

• Оригинальная статья Faber & Jackson
• Пересмотр Гудехусом соотношения Фабера – Джексона