WikiDer > Поле (география)
А поле, в контексте пространственный анализ, географические информационные системы, и географическая информатика, это свойство, заполняющее пространство и изменяющееся в зависимости от пространства, например температура или же плотность.[1] Это использование термина было заимствовано из физика и математика, из-за их сходства с физическими полями, такими как Электромагнитное поле или же Гравитационное поле. Синонимичные термины включают пространственно зависимая переменная (геостатистика), статистическая поверхность ( тематическое картографирование), и Интенсивное свойство (Химия), и скрещивание этих дисциплин является обычным явлением. Простейшей формальной моделью поля является функция, которая дает единственное значение для точки в пространстве (т. Е. т = ж(Икс, у, z) )
Это использование поле не следует путать с Информатика и базы данных, которые также часто используются в географические информационные системы.
Природа и типы полей
Несмотря на то, что основная концепция поля пришла из физики, географы разработали независимые теории, модели данных и аналитические методы. Одна из причин этого очевидного несоответствия заключается в том, что, хотя географические поля могут показывать модели, подобные гравитации и магнетизму, они могут иметь совершенно другую основную природу и создаваться очень разными процессами. Географические поля можно классифицировать по их онтологии или фундаментальной природе следующим образом:
- Природные поля, свойства материи, которые формируются в масштабах ниже человеческого восприятия и, следовательно, кажутся непрерывными в человеческих масштабах, например, температура или влажность почвы.
- Агрегатные поля, статистически построенные свойства совокупных групп индивидов, такие как Плотность населения или покрытие кроны деревьев.
- Сферы потенциала или влияния, которые измеряют концептуальные, нематериальные величины (и, таким образом, наиболее тесно связаны с областями физики), такие как вероятность того, что человек в любом данном месте предпочтет использовать конкретный продуктовый магазин.
Географические поля также можно классифицировать в соответствии с типом области измерения измеряемой переменной, которая определяет характер пространственного изменения. А непрерывное поле имеет непрерывную (действительную) область и обычно показывает постепенные изменения в пространстве, такие как температура или влажность почвы; а дискретное поле, также известный как категоричное покрытие, имеет дискретную (часто качественную) область, такую как тип земного покрова, класс почвы или поверхностные геологические образования, и обычно имеет структуру областей однородного значения с границами (или переходными зонами), где значение изменяется.
Обе скаляр (имеющий одно значение для любого местоположения) и вектор (с несколькими значениями для любого местоположения, представляющими разные, но связанные свойства) поля встречаются в географических приложениях, хотя первое более распространено.
Географические поля могут существовать как во временной области, так и в пространстве. Например, температура меняется во времени, а также в зависимости от местоположения в пространстве. Фактически, многие методы, используемые в время география и аналогичные пространственно-временные модели рассматривают местоположение человека как функцию или поле во времени.
История и методы
Моделирование и анализ полей в географических приложениях были разработаны в пяти существенно отдельных направлениях, которые в последние годы постепенно интегрировались.
- Картографические методы визуализации полей, в том числе хороплет и изарифмический карты.
- В количественная революция географии, начиная с 1950-х годов и ведущей к современной дисциплине пространственный анализ; особенно методы, такие как Модель гравитации.
- Развитие растр ГИС-модели и программное обеспечение, начиная с Канадская географическая информационная система в 1960-х годах, которые картировали такие поля, как тип земного покрова.[2]
- Техника картографическое моделирование, впервые Иэн МакХарг в 1960-х[3] и позже формализована для цифровой реализации Даной Томлин как алгебра карт.[4]
- Геостатистика, возникшие в результате геологии с 1950-х гг.[5]
Поля полезны в географическом мышлении и анализе, потому что, когда свойства меняются в пространстве, они имеют тенденцию делать это в пространственных моделях из-за лежащих в основе пространственных структур и процессов. Общая закономерность, согласно Tobler's первый закон географии: «Все связано со всем остальным, но близкие вещи более связаны, чем далекие».[6] То есть поля (особенно те, которые встречаются в природе) имеют тенденцию постепенно меняться, а близлежащие местоположения имеют аналогичные значения. Эта концепция была формализована как пространственная зависимость или же пространственная автокорреляция, лежащий в основе метода геостатистика.[7] Параллельная концепция, получившая меньшую огласку, но лежащая в основе географической теории по крайней мере с тех пор, как Александр фон Гумбольдт является пространственная ассоциация, который описывает сходное распределение явлений.[8] Это понятие регулярно используется в методе алгебра карт.
Модели представления
Поскольку теоретически поле состоит из бесконечного числа значений в бесконечном количестве местоположений, демонстрирующих непараметрический образец, только конечные представления на основе выборки могут использоваться в инструментах анализа и визуализации, таких как ГИС, статистика и карты. . Таким образом, появилось несколько концептуальных, математических моделей и моделей данных, в том числе:
- An точечный образец неправильной формы, конечный набор выборочных местоположений, либо в случайных, либо в стратегических местах. Примеры включают данные с метеостанций или Лидар облака точек.
- А решетка, или обычная точечная выборка, состоящая из точек, равномерно расположенных в каждом декартовом направлении. Обычно они хранятся в Растровые данные структура. Примеры включают Цифровая модель рельефа.
- А Хороплет, нерегулярный априори раздел, в котором пространство разделено на регионы, не связанные с самим полем, например страны, а значения полей суммируются по каждому региону. Обычно они хранятся с использованием вектор полигоны. Примеры включают Плотность населения по округам на основе результатов переписи.
- А Цветная карта или же Карта класса площади, нерегулярное стратегическое разделение, обычно используемое для дискретных полей, в котором пространство разделено на области, предназначенные для соответствия областям с однородным значением поля, обычно хранящимся в виде векторных многоугольников. Примеры включают карты геологических слоев или насаждений растительности.
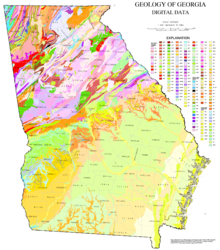 Геологическая карта Грузия, хорохроматическая карта поля поверхностная геологическая формация.
Геологическая карта Грузия, хорохроматическая карта поля поверхностная геологическая формация. - А сетка или обычный раздел, в котором пространство разделено на равные области (часто квадраты), а значения полей суммируются по каждой области. Они также обычно хранятся в Растровые данные структура. Примеры включают сигнатура электромагнитного отражения земного покрова, как представлено в Дистанционное зондирование образы.
- А поверхность, в котором поле концептуализируется как третье пространственное измерение, а для представления используются трехмерные модели данных. Примеры включают Триангулированная нерегулярная сеть (БАНКА).
- An изарифм или же изоплета, в котором нарисованы линии, соединяющие местоположения с одинаковым значением поля, разделяя пространство на области с одинаковым значением. Примером может служить Контурная линия высоты, обычно встречающейся на топографических картах.
 Топографическая карта из Стоу, Вермонт. Коричневые контурные линии представляют высота. Расстояние между контурами 20 ноги.
Топографическая карта из Стоу, Вермонт. Коричневые контурные линии представляют высота. Расстояние между контурами 20 ноги.
Выбор модели представления обычно зависит от множества факторов, включая концептуальную модель явления аналитика, устройства или методы, доступные для измерения поля, инструменты и методы, доступные для анализа или визуализации поля, а также модели, используемые для другие явления, с которыми будет интегрировано рассматриваемое поле. Основная проблема связана с необходимостью Интерполяция для оценки значений полей между точками отбора проб или внутри них, что может привести к ряду форм неопределенности или неправильной интерпретации, например Экологическая ошибка и Задача изменяемой площади. Это также означает, что при преобразовании данных из одной модели в другую (например, создание ЦМР из облака точек лидара) результат будет менее определенным, чем исходный.
Рекомендации
- ^ Пёке, Донна Дж., Барри Смит, Берит Брогаард, изд. Онтология полей, Отчет о встрече специалистов, проведенной в рамках проекта Варениус, 11-13 июня 1998 г., 1999
- ^ Фишер, Терри и Конни Макдональд, Обзор Канадской географической информационной системы (CGIS), Труды Auto-Carto IV, Картография и географическое информационное общество, 1979 г.
- ^ МакХарг, Ян, Дизайн с природой, Американский музей естественной истории, 1969 г.
- ^ Томлин, К. Дана, Геоинформационные системы и картографическое моделирование Прентис-Холл 1990.
- ^ Гриффит, Дэниел А., Пространственная статистика: взгляд количественного географа, Пространственная статистика, 1: 3-15, DOI: 10.1016 / j.spasta.2012.03.005
- ^ Тоблер В. (1970) «Компьютерный фильм, имитирующий рост городов в районе Детройта». Экономическая география, 46 (Приложение): 234–240.
- ^ Клифф, А. и Дж. Орд, Пространственная автокорреляция, Пион, 1973
- ^ Брэдли Миллер Основы пространственного прогнозирования www.geographer-miller.com, 2014 г.


