WikiDer > Обобщенная география
В теория сложности вычислений, обобщенная география хорошо известный PSPACE-полный проблема.
Введение
География это детский игра, что хорошо для длительной автомобильной поездки, когда игроки по очереди называют города из любой точки мира. Каждый выбранный город должен начинаться с той же буквы, что и предыдущее название города. Повторение не допускается. Игра начинается с произвольного начального города и заканчивается, когда игрок проигрывает, потому что не может продолжить игру.
Графическая модель
Чтобы визуализировать игру, ориентированный граф могут быть построены, узлами которых являются все города мира. Стрелка добавляется из узла N1 узел N2 тогда и только тогда, когда городская маркировка N2 начинается с буквы, оканчивающей название узла маркировки города N1. Другими словами, мы рисуем стрелку из одного города в другой, если первый по правилам игры может вести ко второму. Каждое альтернативное ребро в ориентированном графе соответствует каждому игроку (для игры вдвоем). Первый игрок, не сумевший продолжить путь, проигрывает. Иллюстрация игры (с некоторыми городами в Мичигане) показана на рисунке ниже.
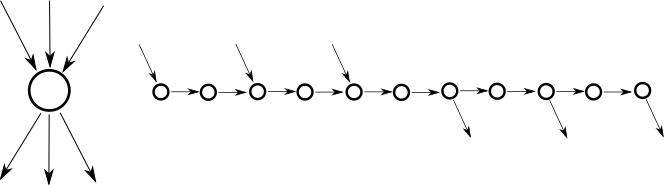
В игре по обобщенной географии (GG) мы заменяем граф названий городов произвольным ориентированным графом. Следующий график представляет собой пример игры по обобщенной географии.
Играя в игру
Мы определяем п1 когда игрок двигается первым и п2 как игрок движется вторым и назовите узлы N1 к Nп. На приведенном выше рисунке п1 имеет следующую выигрышную стратегию: N1 указывает только на узлы N2 и N3. Таким образом п1Первый ход должен быть одним из этих двух вариантов. п1 выбирает N2 (если п1 выбирает N3, тогда п2 выберут N9 так как это единственный вариант и п1 проиграет). Следующий п2 выбирает N4 потому что это единственный оставшийся выбор. п1 теперь выбирает N5 и п2 впоследствии выбирает N3 или N7. Вне зависимости от п2'выбор, п1 выбирает N9 и п2 не имеет оставшихся вариантов и проигрывает игру.
Вычислительная сложность
Проблема определения того, у какого игрока есть выигрышная стратегия в обобщенной географической игре: PSPACE-полный.
Обобщенная география в PSPACE
Пусть GG = {<г, б> | п1 имеет выигрышную стратегию для общей географической игры на графике г начиная с узла б }; чтобы показать, что GG ∈ PSPACE, мы представляем рекурсивный алгоритм в полиномиальном пространстве, определяющий, у какого игрока есть выигрышная стратегия. Учитывая экземпляр GG, <г, пНачните> где г ориентированный граф и пНачните - назначенный начальный узел, алгоритм M происходит следующим образом:
На M(<г, пНачните>):
- Измерьте степень выхода узла пНачните. Если эта степень равна 0, то верните отвергать, потому что для первого игрока нет доступных ходов.
- Составьте список всех узлов, доступных из пНачните по одному краю: п1, п2, ..., пя.
- удалять пНачните и все ребра, соединенные с ним из г формировать г1.
- Для каждого узла пj в списке п1, ..., пя, вызов M(<г1, пj>).
- Если все эти звонки вернутся принять, то независимо от того, какое решение п1 делает, п2 имеет стратегию победы, так что вернись отвергать. В противном случае (если один из вызовов вернет отвергать) п1 имеет выбор, который отрицает любые успешные стратегии п2так что вернись принять.
Алгоритм M однозначно решает ГГ. Он находится в PSPACE поскольку единственная используемая неочевидная полиномиальная рабочая область находится в стеке рекурсии. Пространство, занимаемое стеком рекурсии, является полиномиальным, потому что каждый уровень рекурсии добавляет один узел в стек, и существует не более п уровни, где п количество узлов в г. По сути, это эквивалентно поиск в глубину.
Обобщенная география сложна для PSPACE
Следующее доказательство принадлежит Дэвиду Лихтенштейну и Майклу Сипсеру.[1]
Для создания PSPACE-твердость GG можно уменьшить ФОРМУЛА-ИГРА проблема (которая, как известно, PSPACE-жесткий) в GG за полиномиальное время (п). Короче говоря, пример задачи FORMULA-GAME состоит из количественная логическая формула φ = ∃Икс1 ∀Икс2 ∃Икс3 ...Qxk(ψ) где Q либо ∃, либо ∀. В игру играют два игрока, па и пе, которые чередуют выбор значений для следующих друг за другом Икся. пе выигрывает, если формула ψ заканчивается правда, и па выигрывает, если ψ заканчивается ложный. Предполагается, что формула ψ принадлежит конъюнктивная нормальная форма.
В этом доказательстве мы предполагаем, что список кванторов начинается и заканчивается экзистенциальным квалификатором для простоты. Обратите внимание, что любое выражение можно преобразовать в эту форму, добавив фиктивные переменные, которых нет в ψ.
Построив граф г подобно показанному выше, мы покажем, что любой экземпляр FORMULA-GAME можно свести к экземпляру Generalized Geography, где оптимальная стратегия для п1 эквивалентно пе, и оптимальная стратегия для п2 эквивалентно па.
Левая вертикальная цепочка узлов предназначена для имитации процедуры выбора значений переменных в FORMULA-GAME. Каждая структура алмаза соответствует определенной количественной переменной. Игроки по очереди выбирают пути в каждом узле ветвления. Поскольку мы предположили, что первый квантор будет экзистенциальным, п1 идет первым, выбирая левый узел, если Икс1 является правда и правый узел, если Икс1 является ложный. Затем каждый игрок должен сделать принудительный ход, а затем п2 выбирает значение для Икс2. Эти чередующиеся назначения продолжаются по левой стороне. После того, как оба игрока пройдут через все бриллианты, снова п1 В свою очередь, потому что мы предположили, что последний квантор экзистенциальный. п1 нет другого выбора, кроме как следовать по пути к правой части графика. Тогда это п2 очередь сделать ход.
Когда игра попадает в правую часть графика, это похоже на конец игры в игре по формулам. Напомним, что в игре по формулам пе выигрывает, если ψ правда, в то время как па выигрывает, если ψ ложный. Правая часть графика гарантирует, что п1 побеждает тогда и только тогда, когда пе побеждает, и это п2 побеждает тогда и только тогда, когда па побеждает.
Сначала покажем, что п2 всегда побеждает, когда па побеждает. Если па выигрывает, ψ ложный. Если ψ ложный, существует неудовлетворительная оговорка. п2 выберет неудовлетворительную статью, чтобы выиграть. Тогда, когда это п1в свою очередь, он должен выбрать буквальное значение в этом предложении, выбранном п2. Поскольку все литералы в предложении ложный, они не подключаются к ранее посещенным узлам в левой вертикальной цепочке. Это позволяет п2 проследить подключение к соответствующему узлу в ромбе левой цепочки и выбрать его. Однако, п1 теперь не может выбрать соседние узлы и проигрывает.
Теперь покажем, что п1 всегда побеждает, когда пе побеждает. Если пе выигрывает, ψ правда. Если ψ правда, каждое предложение в правой части графа содержит правда буквальный. п2 можете выбрать любой пункт. потом п1 выбирает буквальный правда. И потому что это правда, соседний с ним узел в левом вертикальном узле уже выбран, поэтому п2 не имеет ходов и проигрывает.
Планарная обобщенная география является PSPACE-полной
Обобщенная география полностью соответствует PSPACE, даже если играть на планарные графы. Следующее доказательство взято из теоремы 3 из.[1]
Так как планарный GG является частным случаем GG, а GG находится в PSPACE, поэтому планарный GG находится в PSPACE. Осталось показать, что планарный ГГ PSPACE-сложен. Это можно доказать, показав, как преобразовать произвольный граф в планарный, так что игра GG, сыгранная на этом графе, будет иметь тот же результат, что и на исходном графе.
Для этого нужно всего лишь удалить все пересечения ребер исходного графа. Мы рисуем граф так, чтобы никакие три ребра не пересекались в одной точке, и никакая пара пересекающихся ребер не могла использоваться в одной игре. Обычно это невозможно, но всегда возможно для графа, построенного из экземпляра FORMULA-GAME; например, мы могли бы иметь только ребра из вершин предложения, участвующих в пересечениях. Теперь заменим каждый перекресток этой конструкцией:
В результате получается планарный граф, и тот же игрок может добиться победы, как и в исходном графе: если игрок решает двигаться «вверх» от V в преобразованной игре, то оба игрока должны продолжать движение «вверх» до W или проиграть. немедленно. Таким образом, движение «вверх» от V в преобразованной игре имитирует движение V → W в исходной игре. Если V → W является выигрышным ходом, то движение «вверх» от V в преобразованной игре также является выигрышным ходом, и наоборот.
Таким образом, игра GG на преобразованном графе будет иметь тот же результат, что и на исходном графе. Это преобразование требует времени, которое является постоянным кратным количеству пересечений ребер в исходном графе, поэтому оно занимает полиномиальное время.
Таким образом, планарный GG является PSPACE-полным.
Плоский двудольный граф с максимальной степенью 3
GG играл на планарном двудольные графы с максимальной степенью 3 остается PSPACE-полным, если заменить вершины степени выше 3 цепочкой вершин со степенью не выше 3. Доказательство.[1] и использует следующую конструкцию:
Если один игрок использует любой из входов в эту конструкцию, другой игрок выбирает, какой выход будет использован. Также конструкция может быть пройдена только один раз, потому что центральная вершина посещается всегда. Следовательно, эта конструкция эквивалентна исходной вершине.
География края
Вариант GG называется география края, где после каждого хода стирается грань, которую прошел игрок. В этом отличие от оригинальной GG, где после каждого хода вершина, на которой раньше находился игрок, стирается. С этой точки зрения исходный GG можно назвать География вершин.
География края - полная PSPACE. Это можно доказать, используя ту же конструкцию, которая использовалась для географии вершин.[2]
Неориентированная география
Можно также рассмотреть возможность сыграть в игру по географии на неориентированный граф (то есть края можно перемещать в обоих направлениях). Френкель, Шайнерман и Ульман[3] покажи это неориентированная география вершин можно решить за полиномиальное время, тогда как ненаправленная география края является PSPACE-полным даже для плоских графов с максимальной степенью 3. Если граф двудольный, то неориентированная география ребер разрешима за полиномиальное время.
Последствия
Учитывая, что GG PSPACE-полный, не существует алгоритма полиномиального времени для оптимальной игры в GG, если только п = PSPACE. Однако доказать сложность других игр может быть не так просто, потому что некоторые игры (например, шахматы) содержат конечное количество игровых позиций, что затрудняет (или делает невозможным) определение отображения на PSPACE-полный проблема. Несмотря на это, сложность некоторых игр все же может быть проанализирована путем обобщения (например, п × п доска). См. Ссылки для доказательства обобщенного Идти, как следствие доказательства полноты GG.
использованная литература
- ^ а б c Лихтенштейн, Дэвид; Сипсер, Майкл (апрель 1980 г.). «Go Is Polynomial-Space Hard» (PDF). Журнал ACM. 27 (2): 393–401. Дои:10.1145/322186.322201.
- ^ Шефер, Томас Дж. (1978). «О сложности некоторых игр с идеальной информацией для двух человек». Журнал компьютерных и системных наук. 16 (2): 185–225. Дои:10.1016/0022-0000(78)90045-4.
- ^ Френкель, Авиезри; Шайнерман, Эдвард; Ульман, Даниэль (1993). «География ненаправленного края». Теоретическая информатика. 112 (2): 371–381. Дои:10.1016 / 0304-3975 (93) 90026-п.