WikiDer > Комета Гольдбаха - Википедия
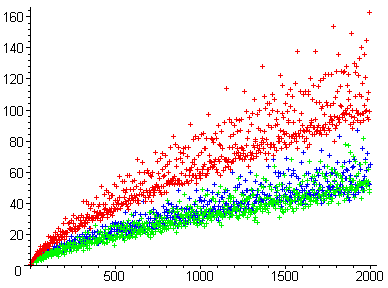
Комета Гольдбаха[1] имя, данное графику функции , так называемой Функция Гольдбаха. Функция Гольдбаха изучается относительно Гипотеза Гольдбаха. Функция определено для всех четных целых чисел быть количеством различных способов, которыми E можно выразить как сумму двух простых чисел. Например, поскольку 22 можно выразить как сумму двух простых чисел тремя разными способами ().
Раскраска точек на изображении выше основана на значении по модулю 3 с красными точками, соответствующими 0 mod 3, синими точками, соответствующими 1 mod 3, и зелеными точками, соответствующими 2 mod 3. Другими словами, красные точки кратны 6; синие точки имеют форму «кратное 6 плюс 2»; а зеленые точки кратны 6 плюс 4.
Анатомия кометы Гольдбаха
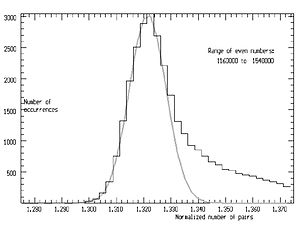
Яркий способ представления данных о кометах - это как гистограмма. Функция может быть нормализовано делением на локально усредненное значение грамм, граммсредний, взятое за возможно 1000 соседних значений четного числа E. Затем гистограмму можно накапливать в диапазоне примерно до 10% по обе стороны от центрального E.
Такая гистограмма появляется справа. Видна серия четко определенных пиков. Каждый из этих пиков можно идентифицировать как сформированный набором значений которые имеют определенные наименьшие факторы. Основные пики соответствуют самым низким коэффициентам 3, 5, 7 ... как указано. По мере того, как самые низкие коэффициенты становятся выше, пики перемещаются влево и в конечном итоге сливаются, давая первичный пик самого низкого значения.
Фактически существует иерархия пиков; основные пики состоят из вспомогательных пиков, с последовательностью вторых по величине факторов . Эта иерархия продолжается до тех пор, пока не будут исчерпаны все факторы.
Увеличенный разрез более подробно показывает последовательность дополнительных пиков.
Взаимное расположение пиков следует из формы, разработанной Харди и Литтлвудом:[2]
где произведение берется по всем простым числам п это факторы . Коэффициент справа равен Двойная простая постоянная Харди – Литтлвуда
Здесь произведение берется по всем простым числам больше 2.
Особый интерес представляет пик, образованный выбором только значений это основные. Тогда коэффициент произведения в уравнении (1) очень близок к 1. Пик очень близок к гауссовой форме (показан серым). Для этого диапазона E значений, положение пика находится в пределах 0,03% от идеального .
При формировании гистограмм для разных средних значений Eширина этого пика (только для простых чисел) оказывается пропорциональной . Однако это примерно в 1,85 раза меньше, чем значение этого можно было бы ожидать от гипотезы полностью случайный совпадение простых пар. Этого можно ожидать, так как есть корреляции которые приводят к разделению пиков на общей гистограмме.
Возвращаясь к полному спектру а не просто простые числа, видно, что другие пики, связанные с указанными наименьшими факторами так же может быть приспособленный по Гауссовский, но только на нижнем плече. Верхнее плечо, образованное совокупностью вспомогательных пиков, лежит выше простой гауссовой формы.
Относительные высоты пиков на общей гистограмме репрезентативны для популяций различных типов имея разные факторы. Высота примерно обратно пропорциональна , продукты самых низких факторов. Таким образом, высота пика, отмеченного (3,5) на общей гистограмме, составляет примерно 1/15 от основного пика. Высота может отличаться примерно на 20%; их точное значение является сложной функцией того, как пики состоят из их компонентов, и их переменной ширины.
Интересно порассуждать о возможности любого числа E имея нулевые пары простых чисел, принимая эти гауссовские формы как вероятности, и если предположить, что экстраполировать в точку нулевой пары. Если это будет сделано, вероятность нулевых пар для любой из Eв рассматриваемом диапазоне порядка 10−3700. Интегральная вероятность по всем E до бесконечности с учетом сужения ширины пика не намного больше. Можно разумно ожидать, что любой поиск нарушения гипотезы Гольдбаха приведет к снижению этих шансов.
Рекомендации
- ^ Флигель, Генри Ф .; Робертсон, Дуглас С .; «Комета Гольдбаха: числа, связанные с гипотезой Гольдбаха»; Журнал развлекательной математики, v21 (1) 1-7, 1989.
- ^ Г. Х. Харди и Дж. Э. Литтлвуд, "Некоторые проблемы 'partitio numerorum'; III: о выражении числа как суммы простых чисел", Acta Mathematica, т. 44, стр. 1-70, 1922.