WikiDer > Серый график
| Серый график | |
|---|---|
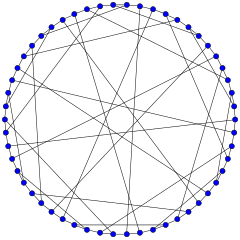 Серый график | |
| Названный в честь | Мэрион Кэмерон Грей |
| Вершины | 54 |
| Края | 81 |
| Радиус | 6 |
| Диаметр | 6 |
| Обхват | 8 |
| Автоморфизмы | 1296 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический Полусимметричный Гамильтониан Двудольный |
| Таблица графиков и параметров | |
в математический поле теория графов, то Серый график является ненаправленный двудольный граф с 54 вершины и 81 края. Это кубический граф: каждая вершина касается ровно трех ребер. Это было обнаружено Мэрион С. Грей в 1932 г. (не опубликовано), а затем независимо обнаружил Бауэр в 1968 г. в ответ на вопрос, заданный Джон Фолкман 1967. Граф Грея интересен как первый известный пример кубического графа, обладающего алгебраическим свойством быть реберным, но не вершинно-транзитивным (см. Ниже).
Серый график имеет хроматическое число 2, хроматический индекс 3, радиус 6 и диаметр 6. Это также 3-вершинно-связанный и 3-реберный неплоский граф.
Строительство
Граф Грея можно построить (Бауэр 1972) из 27 точек сетки 3 × 3 × 3 и 27 линий, параллельных осям, проходящих через эти точки. Этот набор точек и линий образует проективная конфигурация: каждая точка проходит через ровно три линии, и каждая линия имеет ровно три точки. Серый график - это Граф Леви этой конфигурации; у него есть вершина для каждой точки и каждой линии конфигурации и ребро для каждой пары точки и линии, которые касаются друг друга. Эта конструкция обобщает (Bouwer 1972) на любое измерение п ≥ 3, что дает п-валентный граф Леви с алгебраическими свойствами, подобными таковым у графа Грея. В (Monson, Pisanski, Schulte, Ivic-Weiss 2007) граф Грея появляется как другой вид графа Леви для ребер и треугольных граней некоторого локально тороидального абстрактного регулярного 4-многогранника. Таким образом, он является первым в бесконечном семействе аналогичных кубических графов. Как и другие графы Леви, это двудольный граф, с вершинами, соответствующими точкам с одной стороны от двухраспределения, и вершинами, соответствующими линиям с другой стороны.
Марушич и Писанский (2000) дают несколько альтернативных методов построения графа Грея. Как и в любом двудольном графе, нет нечетной длины циклы, а также нет циклов из четырех или шести вершин, поэтому обхват графа Грея равно 8. Простейшая ориентированная поверхность, на которую можно вложить граф Грея, имеет род 7 (Марушич, Писански и Уилсон 2005).
Серый график Гамильтониан и может быть построен из Обозначение LCF:
Как гамильтонов кубический граф, он имеет хроматический индекс три.
Алгебраические свойства
В группа автоморфизмов графа Грея представляет собой группу порядка 1296. Она действует транзитивно на ребрах графа, но не на его вершинах: есть симметрии переводит каждое ребро в любое другое, но не переводит каждую вершину в любую другую вершину. Вершины, соответствующие точкам базовой конфигурации, могут быть симметричны только другим вершинам, которые соответствуют точкам, а вершины, соответствующие линиям, могут быть симметричными только другим вершинам, которые соответствуют линиям. Следовательно, граф Грея - это полусимметричный граф, наименьший возможный кубический полусимметричный граф.
Характеристический многочлен графа Грея равен
Рекомендации
- Бауэр, И. З. (1968), "Реберный, но не вершинный транзитивный кубический граф", Канадский математический бюллетень, 11 (4): 533–535, Дои:10.4153 / CMB-1968-063-0.
- Бауэр, И. З. (1972), "О реберных, но не вершинных транзитивных регулярных графах", Журнал комбинаторной теории, серия B, 12: 32–40, Дои:10.1016/0095-8956(72)90030-5.
- Фолькман, Дж. (1967), "Правильные линейно-симметричные графы", Журнал комбинаторной теории, 3 (3): 533–535, Дои:10.1016 / S0021-9800 (67) 80069-3.
- Марушич, Драган; Писанский, Томаж (2000), «Новый взгляд на серый график», Журнал теории графов, 35: 1–7, Дои:10.1002 / 1097-0118 (200009) 35: 1 <1 :: AID-JGT1> 3.0.CO; 2-7.
- Марушич, Драган; Писанский, Томаж; Уилсон, Стив (2005), «Род графа Грея равен 7», Европейский журнал комбинаторики, 26 (3–4): 377–385, Дои:10.1016 / j.ejc.2004.01.015.
- Monson, B .; Писанский, Т.; Schulte, E .; Ivic-Weiss, A. (2007), "Полусимметричные графы из многогранников", Журнал комбинаторной теории, серия А, 114 (3): 421–435, arXiv:математика / 0606469, Дои:10.1016 / j.jcta.2006.06.007, S2CID 10203794


![[-25,7,-7,13,-13,25]^{9}.\](https://wikimedia.org/api/rest_v1/media/math/render/svg/014e670206b76bab2513b807e955533d50c3efb0)
