WikiDer > Большой перевернутый курносый икосододекаэдр
| Большой перевернутый курносый икосододекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 92, E = 150 V = 60 (χ = 2) |
| Лица по сторонам | (20+60){3}+12{5/2} |
| Символ Wythoff | | 5/3 2 3 |
| Группа симметрии | Я, [5,3]+, 532 |
| Указатель ссылок | U69, C73, W116 |
| Двойной многогранник | Большой перевернутый пятиугольный гексаконтаэдр |
| Фигура вершины |  34.5/3 |
| Акроним Bowers | Гисид |
В геометрия, то большой перевернутый курносый икосододекаэдр (или же большой вертиснуб икосододекаэдр) это однородный звездный многогранник, индексируется как U69. Дается Символ Шлефли sr {5⁄3, 3} и Диаграмма Кокстера-Дынкина ![]()
![]()
![]()
![]()
![]()
![]()
![]() . В книге Модели многогранников к Магнус Веннингер, многогранник неправильно назван большой курносый икосододекаэдр, наоборот.
. В книге Модели многогранников к Магнус Веннингер, многогранник неправильно назван большой курносый икосододекаэдр, наоборот.
Декартовы координаты
Декартовы координаты для вершин большого перевернутого курносого икосододекаэдра все даже перестановки из
- (± 2α, ± 2, ± 2β),
- (± (α − βτ − 1 / τ), ± (α / τ + β − τ), ± (−ατ − β / τ − 1)),
- (± (ατ − β / τ + 1), ± (−α − βτ + 1 / τ), ± (−α / τ + β + τ)),
- (± (ατ − β / τ − 1), ± (α + βτ + 1 / τ), ± (−α / τ + β − τ)) и
- (± (α − βτ + 1 / τ), ± (−α / τ − β − τ), ± (−ατ − β / τ + 1)),
с четным числом плюсов, где
- α = ξ − 1 / ξ
и
- β = −ξ / τ + 1 / τ2−1 / (ξτ),
где τ = (1+√5) / 2 - это Золотая середина а ξ - большее положительное вещественное решение ξ3−2ξ = −1 / τ, или приблизительно 1,2224727. нечетные перестановки приведенных выше координат с нечетным числом знаков плюс дает другую форму, энантиоморф другого.
Радиус описанной окружности для единицы длины кромки равен
куда соответствующий корень . Четыре положительных реальных корня секстический в
окружные радиусы курносый додекаэдр (U29), большой курносый икосододекаэдр (U57), большой перевернутый курносый икосододекаэдр (U69), и большой ретроснуб икосододекаэдр (U74).
Связанные многогранники
Большой перевернутый пятиугольный гексаконтаэдр
| Большой перевернутый пятиугольный гексаконтаэдр | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо | 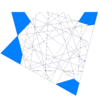 |
| Элементы | F = 60, E = 150 V = 92 (χ = 2) |
| Группа симметрии | Я, [5,3]+, 532 |
| Указатель ссылок | DU69 |
| двойственный многогранник | Большой перевернутый курносый икосододекаэдр |
В большой перевернутый пятиугольный гексеконтаэдр (или же лепестковый трисикосаэдр) невыпуклый равногранный многогранник. Он состоит из 60 вогнутый пятиугольные грани, 150 ребер и 92 вершины.
Это двойной из униформа большой перевернутый курносый икосододекаэдр.
Пропорции
Обозначим Золотое сечение к . Позволять наименьший положительный нуль многочлена . Тогда каждая пятиугольная грань имеет четыре равных угла и один угол . Каждая грань имеет три длинных и два коротких края. Соотношение между длинами длинного и короткого краев определяется выражением
- .
В двугранный угол равно . Часть каждой грани находится внутри твердого тела, поэтому в твердотельных моделях не видна. Два других нуля многочлена играют аналогичную роль в описании большой пятиугольный гексеконтаэдр и большой пентаграмматический гексеконтаэдр.
Смотрите также
Рекомендации
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, ISBN 978-0-521-54325-5, МИСТЕР 0730208 п. 126
внешняя ссылка
- Вайсштейн, Эрик В. «Большой перевернутый пятиугольный гексаконтаэдр». MathWorld.
- Вайсштейн, Эрик В. «Большой перевернутый курносый икосододекаэдр». MathWorld.
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |















