WikiDer > Граф Харриса
| Граф Харриса | |
|---|---|
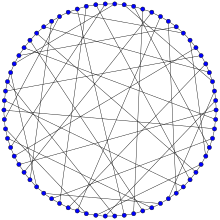 Граф Харриса | |
| Вершины | 70 |
| Края | 105 |
| Радиус | 6 |
| Диаметр | 6 |
| Обхват | 10 |
| Автоморфизмы | 120 (S5) |
| Хроматическое число | 2 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Кубический Клетка Без треугольников Гамильтониан |
| Таблица графиков и параметров | |
в математический поле теория графов, то Граф Харриса или же Харрис (3-10) -клетка это 3-обычный неориентированный граф с 70 вершинами и 105 ребрами.[1]
Граф Харриса имеет хроматическое число 2, хроматический индекс 3, радиус 6, диаметр 6, обхват 10 и составляет Гамильтониан. Это также 3-вершинно-связанный и 3-реберный непланарный кубический граф. Она имеет толщина книги 3 и номер очереди 2.[2]
В характеристический многочлен графа Харриса
История
В 1972 г. А. Т. Балабан опубликовал (3-10) -клетка, кубический граф с минимальным количеством вершин для обхвата 10.[3] Это была первая (3-10) обнаруженная клетка, но она не была уникальной.[4]
Полный список (3-10) -клеток и доказательство минимальности были даны О'Кифом и Вонгом в 1980 году.[5] Существует три различных (3-10) -клеточных графа - Балабан 10-клеточный, граф Харриза и График Харриса – Вонга.[6] Более того, граф Харриса – Вонга и граф Харриза являются кососпектральные графики.
Галерея
Рекомендации
- ^ Вайсштейн, Эрик В. "График Харриса". MathWorld.
- ^ Джессика Вольц, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ А. Т. Балабан, трехвалентный граф обхвата десять, J. Combin. Теория Сер. В 12, 1-5. 1972 г.
- ^ Писанский, Т .; Boben, M .; Марушич, Д .; и Орбанич, А. "Обобщенные конфигурации Балабана". Препринт. 2001 г. [1].
- ^ М. О'Киф и П.К. Вонг, Наименьший граф обхвата 10 и валентности 3, J. Combin. Теория Сер. В 29 (1980) 91-105.
- ^ Бонди, Дж. А., Мурти, США. Теория графов с приложениями. Нью-Йорк: Северная Голландия, стр. 237, 1976.




