WikiDer > Формула длины крючка - Википедия
В комбинаторная математика, то формула длины крючка это формула для количества стандартные картины Юнга чья форма дана Диаграмма Юнга.Он имеет приложения в различных области Такие как теория представлений, вероятность, и анализ алгоритма; например, проблема самые длинные возрастающие подпоследовательности. Связанная формула подсчитывает количество полустандартных таблиц Юнга, которые являются специализацией Полином Шура.
Определения и заявление
Позволять быть раздел из .Принято толковать графически как Диаграмма Юнга, а именно выровненный по левому краю массив квадратных ячеек с ряды длин .A (стандарт) Молодая картина формы это наполнение ячейки диаграммы Юнга со всеми целыми числами , без повторения, так что каждая строка и каждый столбец образуют возрастающие последовательности. , в й ряд и -й столбец крюк это набор ячеек такой, что и или же и .Длина крючка. количество ячеек в .
Формула длины крючка выражает количество стандартных таблиц формы Юнга. , обозначаемый или же , так как
где продукт по всем ячейкам диаграммы Юнга.
Примеры
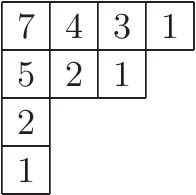
На рисунке справа показаны длины крючков для ячеек в Диаграмма Юнга , соответствующий разбиению 9 = 4 + 3 + 1 + 1. Формула длины крюка дает количество стандартных таблиц Юнга как:
А Каталонский номер считает пути Дика с шаги вверх (U) с вкраплениями шаги вниз (D), так что на каждом шаге никогда не бывает больше D, чем U. Они находятся в противоречии с таблицами форм Юнга. : путь Дика соответствует таблице, в первой строке которой перечислены позиции U-ступеней, а во второй строке - позиции D-ступеней. Например, UUDDUD соответствуют таблицам со строками 125 и 346.
Это показывает, что , поэтому формула крючка специализируется на хорошо известной формуле продукта
История
Есть и другие формулы для , но формула длины крючка особенно проста и элегантна. Менее удобная формула, выражающая с точки зрения детерминант был выведен независимо Фробениус и Молодой в 1900 и 1902 годах соответственно с использованием алгебраических методов.[1][2]MacMahon нашел альтернативное доказательство формулы Юнга – Фробениуса в 1916 г., используя разностные методы.[3]
Сама формула длины крючка была открыта в 1953 году Фреймом. Робинсон, и Тралл как улучшение формулы Юнга – Фробениуса. Саган[4] описывает открытие следующим образом.
Однажды в четверг мая 1953 года Робинсон посетил Фрейма в Университете штата Мичиган. Обсуждая работу Стаала (ученика Робинсона), Фрейм пришел к выводу о формуле крючка. Сначала Робинсон не мог поверить, что такая простая формула существует, но, попробовав несколько примеров, он убедился, и вместе они подтвердили идентичность. В субботу они отправились в Мичиганский университет, где Фрейм представил свой новый результат после лекции Робинсона. Это удивило Тралла, который был в зале, потому что он только что доказал тот же результат в тот же день!
Несмотря на простоту формулы длины крючка, доказательство Фрейма – Робинсона – Тралла не очень информативно и не дает никакого интуитивного представления о роли крючков. Поиск краткого, интуитивно понятного объяснения, подходящего к такому простому результату, привел к появлению множества альтернативных доказательств.[5]Хиллман и Грассл дали первое доказательство, проливающее свет на роль крючков, в 1976 году, доказав частный случай Стэнли формула содержания крючка, которая, как известно, подразумевает формулу длины крючка.[6]Грин, Nijenhuis, и Уилф нашел вероятностное доказательство, используя прогулку на крючке, в которой длина крюка появляется естественным образом в 1979 году.[7]Реммель адаптировал исходное доказательство Фрейма – Робинсона – Тралла в первое биективное доказательство для формулы длины крюка в 1982 году.[8]Прямое биективное доказательство было впервые открыто Францблау и Zeilberger в 1982 г.[9]Zeilberger также преобразовал доказательство прогулки по крюку Грина – Нийенхейса – Уилфа в биективное доказательство в 1984 году.[10] Более простая прямая биекция была объявлена Пак и Стояновского в 1992 г., а его полное доказательство было представлено парой и Новелли в 1997 г.[11][12][13]
Между тем, формула длины крючка была обобщена несколькими способами. М. Тралл нашел аналог формулы длины крючка для смещенных таблиц Юнга в 1952 году.[14] Саган предоставил доказательство смещения крюка для формулы длины крюка для смещенных таблиц Юнга в 1980 году.[15] Саган и Йе доказали формулу длины крюка для бинарных деревьев с помощью прогулки на крючке в 1989 году.[16] Проктор дал некоторое обобщение (см. Ниже).
Вероятностное доказательство
Эвристический аргумент Кнута
Формулу длины крюка можно интуитивно понять, используя следующий эвристический, но неверный аргумент, предложенный Д. Э. Кнут.[17]Учитывая, что каждый элемент таблицы является наименьшим в своем крючке и заполняет форму таблицы случайным образом, вероятность того, что ячейка будет содержать минимальный элемент соответствующего крючка, обратно пропорциональный длине крючка. Умножая эти вероятности на все и дает формулу. Этот аргумент ошибочен, поскольку события не являются независимыми.
Однако аргумент Кнута верен для перечисления меток на деревьях, удовлетворяющих свойствам монотонности, аналогичным свойствам таблицы Юнга. В этом случае рассматриваемые события «крючка» фактически являются независимыми событиями.
Вероятностное доказательство с использованием крюковой прогулки
Это вероятностное доказательство, найденное К. Грин, А. Нийенхейс, и Х. С. Вильф в 1979 г.[18] Определять
Мы хотим показать, что . Первый,
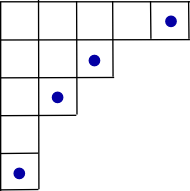
где сумма пробегает все диаграммы Юнга получен из удалив одну угловую ячейку. (Максимальный вход таблицы Юнга формы происходит в одной из его угловых ячеек, поэтому удаление дает таблицы Юнга формы .)
Мы определяем и , поэтому достаточно показать такое же повторение
что означало бы по индукции. Приведенную выше сумму можно рассматривать как сумму вероятностей, записав ее как
Следовательно, нам нужно показать, что числа определить вероятностную меру на множестве диаграмм Юнга с . Это делается конструктивным образом путем определения случайного блуждания, называемого прогулка на крючке, на ячейках диаграммы Юнга , который в конечном итоге выбирает одну из угловых ячеек (которые находятся в взаимно однозначном соответствии с диаграммами для которого ). Ход крюка определяется следующими правилами.
- Выбрать ячейку равномерно случайным образом из клетки. Начните оттуда случайное блуждание.
- Преемник текущей ячейки выбирается равномерно случайным образом из крючка .
- Продолжайте, пока не дойдете до угловой ячейки .
Предложение: Для данной угловой ячейки из , у нас есть
куда .
Учитывая это, суммируя по всем угловым ячейкам дает как заявлено.
Связь с представлениями симметрической группы
Формула длины крючка имеет большое значение в теория представлений симметрической группы , где число как известно, равна размерности комплексного неприводимого представления связано с .
Подробное обсуждение
Комплексные неприводимые представления симметрической группы индексируются разбиениями из (видеть Модуль Specht). Их характеры связаны с теорией симметричных функций через внутреннее произведение Холла:
куда это Функция Шура связано с и является степенной симметричной функцией разбиения связанный с циклической декомпозицией . Например, если тогда .
Поскольку тождественная перестановка имеет форму в обозначении цикла, , формула говорит
Разложение функций Шура по мономиальным симметрическим функциям использует Костка номера:
Затем внутренний продукт с является , потому что . Обратите внимание, что равно , так что от рассмотрения регулярное представительство из , или комбинаторно из Переписка Робинсона – Шенстеда – Кнута.
Расчет также показывает, что:
Это расширение в терминах функций Шура с использованием коэффициентов, заданных внутренним произведением, поскольку Приведенное выше равенство можно доказать, также проверив коэффициенты каждого одночлена с обеих сторон и используя Переписка Робинсона – Шенстеда – Кнута или, более концептуально, глядя на разложение несводимым модули и взятие персонажей. Видеть Двойственность Шура – Вейля.
Доказательство формулы крюка с использованием формулы Фробениуса[19]
По приведенным выше соображениям
так что
куда это Определитель Вандермонда.
Для раздела , определять за . Для дальнейшего нам понадобится как минимум столько же переменных, сколько строк в разделе, поэтому с этого момента мы работаем с переменные .
Каждый термин равно
(Видеть Функция Шура.) Поскольку вектор отличается для каждого раздела, это означает, что коэффициент в , обозначенный , равно . Это известно как Формула характера Фробениуса, что дает одно из самых ранних доказательств.[20]
Осталось только упростить этот коэффициент. Умножение
и
заключаем, что наш коэффициент как
который можно записать как
Последняя сумма равна определителю
который столбец сводится к Определитель Вандермонда, и мы получаем формулу
Обратите внимание, что - длина крючка первого прямоугольника в каждой строке диаграммы Юнга, и это выражение легко преобразуется в желаемый вид : один показывает , где последний продукт пробегает -я строка диаграммы Юнга.
Связь с самыми длинными возрастающими подпоследовательностями
Формула длины крюка также имеет важные приложения для анализа самые длинные возрастающие подпоследовательности в случайных перестановках. Если обозначает равномерно случайную перестановку порядка , обозначает максимальную длину возрастающей подпоследовательности , и обозначает ожидаемое (среднее) значение , Анатолий Вершик и Сергей Керов [21] и независимо Бенджамин Ф. Логан и Лоуренс А. Шепп[22] показал, что когда большой, примерно равно . Это отвечает на вопрос, первоначально заданный Станислав Улам. Доказательство основано на переводе вопроса через Переписка Робинсона – Шенстеда к задаче о предельной форме случайной таблицы Юнга, выбранной согласно Планшерель мера. Поскольку в определение меры Планшереля входит величина формула длины крюка может затем использоваться для выполнения асимптотического анализа предельной формы и, таким образом, также отвечать на исходный вопрос.
Идеи Вершика – Керова и Логана – Шеппа позже были уточнены Джинхо Байком, Перси Дейфтом и Куртом Йоханссоном, которые смогли добиться гораздо более точного анализа предельного поведения максимальной увеличивающейся длины подпоследовательности, доказав важный теперь известный результат как теорема Байка – Дейфта – Йоханссона. Их анализ снова решительно использует тот факт, что имеет ряд хороших формул, хотя вместо формулы длины крюка используется одно из определяющих выражений.
Связанные формулы
Формула числа таблиц фигуры Юнга был первоначально получен из Формула определителя Фробениуса в связи с теорией представлений:[23]
Длину крючков также можно использовать для представления продукта производящей функции для количества обратных плоских секций заданной формы.[24] Если λ является разбиением некоторого целого числа п, обратное плоское разбиение п с формой λ получается заполнением полей диаграммы Юнга неотрицательными целыми числами, так что элементы добавляются к п и не убывают вдоль каждой строки и вниз по каждому столбцу. Длина крючка можно определить как с таблицами Юнга. Если πп обозначает количество обратных плоскостных разбиений п с формой λ, то производящую функцию можно записать как
Стэнли открыл другую формулу для той же производящей функции.[25] В общем, если есть ли какой-нибудь посет с элементов, производящая функция для обратного -partitions это
куда - многочлен такой, что это количество линейные расширения из .
В случае перегородки , мы рассматриваем ч.у.м. в его ячейках, заданных соотношением
- .
Таким образом, линейное расширение - это просто стандартная таблица Юнга, т.е.
Доказательство формулы крючка с использованием формулы Стэнли
Комбинируя две формулы для производящих функций, мы имеем
Обе стороны сходятся внутри диска радиуса один, и следующее выражение имеет смысл для
Было бы жестоко вставлять 1, но правая часть - это непрерывная функция внутри единичного круга, а многочлен непрерывен всюду, поэтому, по крайней мере, мы можем сказать
Применение Правило L'Hôpital раз дает формулу длины крючка
Формула длины крючка полустандартных таблиц
В Полином Шура - производящая функция полустандартного Молодые картины с формой и записи в . Специализируясь на этом дает количество полустандартных таблиц, которые можно записать в единицах длины крючка:
Диаграмма Юнга соответствует для неприводимое представление из специальная линейная группа , а многочлен Шура также является характером диагональной матрицы действуя по этому представлению. Таким образом, указанная выше специализация является размерностью неприводимого представления, а формула является альтернативой более общей Формула размерности Вейля.
Мы можем уточнить это, взяв основную специализацию функции Шура в переменных :
куда для сопряженного разбиения .
Формула перекоса
Существует обобщение этой формулы для перекосов,[26]
где сумма берется возбужденные диаграммы формы и коробки распределены согласно .
Обобщение на d-полные посеты
Диаграммы Юнга можно рассматривать как конечные идеалы порядка в позе , а стандартные таблицы Юнга - их линейные расширения. Роберт Проктор дал обобщение формулы длины крюка для подсчета линейных расширений более широкого класса множеств, обобщающих как деревья, так и косые диаграммы.[27][28]
Рекомендации
- ^ Г. Фробениус. Uber die charaktere der simrischer gruppe, Preuss. &объявление. Нед. сидеть. (1900), 516–534.
- ^ Молодой. Количественный анализ замещения II, Proc. Лондонская математика. Сот., Сер. 1, 35 (1902), 361–397.
- ^ П. А. Мак-Магон. «Комбинаторный анализ», Cambridge Univ. Press, Лондон / Нью-Йорк, 1916; перепечатано Chelsea, New York, 1960.
- ^ Саган, Брюс (2001). Симметричная группа. Представления, комбинаторные алгоритмы и симметричные функции, 2-е издание. Springer-Verlag. ISBN 0-387-95067-2.
- ^ Кнут, Дональд (1973). Искусство программирования, Том 3: Сортировка и поиск, 3-е издание, Addison – Wesley, p. 63
- ^ А. П. Хиллман и Р. М. Грассл. Перегородки обратной плоскости и номера крючков в таблицах, J. Comb. Теория, сер. А 21 (1976), 216–221.
- ^ Грин, К., Нидженхейс, А. и Уилф, Х. С. (1979). Вероятностное доказательство формулы для числа таблиц Юнга заданной формы. Adv. по математике. 31, 104–109.
- ^ J. B. Remmel. Биективные доказательства формул для ряда стандартных таблиц Юнга, линейной и полилинейной алгебры 11 (1982), 45–100.
- ^ Францблау Д. С. и Цейлбергер Д. (1982). Биективное доказательство формулы длины крючка. J. Algorithms3, 317–343.
- ^ Д. Цайльбергер. Биекция коротких крючков, вдохновленная доказательством Грина – Нийенхейса – Уилфа, Discrete Math. 51 (1984), 101–108.
- ^ Пак И. М., Стояновский А. В. (1992). Биективное доказательство формулы длины крючка. Funct. Анал. Приложение 24.
- ^ Новелли Ж.-К., Пак И.М. и Стояновский А.В. (1997). Прямое биективное доказательство формулы длины крючка. Дискретная математика и теоретическая информатика 1, 1997, 53–67.
- ^ Саган, Брюс (2001). Симметричная группа. Представления, комбинаторные алгоритмы и симметричные функции, 2-е издание. Springer-Verlag. ISBN 0-387-95067-2.
- ^ Р. М. Тралл. Комбинаторная проблема, Michigan Math. J. 1 (1952), 81–88.
- ^ Саган, Б. О выборе случайно сдвинутой таблицы Юнга. J. Алгоритмы 1, 3 (1980), 213–234.
- ^ Саган Б. Э., Йе Ю. Н. Вероятностные алгоритмы для деревьев. Фибоначчи Кварт. 27, 3 (1989), 201–208.
- ^ Кнут, Дональд (1973), Искусство программирования, Том 3: Сортировка и поиск, 3-е издание, Эддисон – Уэсли, стр. 63, ISBN 0-201-03803-X.
- ^ Грин, К., Нидженхейс, А. и Уилф, Х. С. (1979). Вероятностное доказательство формулы для числа таблиц Юнга заданной формы. Adv. по математике. 31, 104–109.
- ^ Фултон, Уильям, 1939- (1991). Теория представлений: первый курс. Харрис, Джо, 1951-. Нью-Йорк: Springer-Verlag. С. 49–50. ISBN 0387974954. OCLC 22861245.CS1 maint: несколько имен: список авторов (связь)
- ^ У. Фултон, Дж. Харрис. Теория репрезентации: первый курс Springer-Verlag, Нью-Йорк, 1991
- ^ Вершик, А. М .; Керов, К. В. (1977), "Асимптотика планшеровской меры симметрической группы и предельная форма для таблиц Юнга", Докл. Акад. АН СССР, 233: 1024–1027.
- ^ Б. Ф. Логан, Л. А. Шепп, Вариационная задача для случайных таблиц Юнга, Успехи в математике. 26 (1977), нет. 2, 206–222.
- ^ Кнут, Дональд (1973), Искусство программирования, 3 (1-е изд.), Addison – Wesley, pp. 61–62
- ^ Стэнли, Ричард П. (1971), "Теория и приложения плоских перегородок, 2", Исследования по прикладной математике, 50: 259–279, Дои:10.1002 / sapm1971503259
- ^ Р. П. Стэнли, докторская диссертация "Упорядоченные структуры и перегородки", Гарвардский университет, 1971 г.
- ^ Моралес, А. Х., Пак, И., и Панова, Г. формулы крюка для косых форм I. q-аналоги и биекции, Журнал комбинаторной теории, сер. А, т. 154 (2018), 350-405.
- ^ Проктор, Роберт (1999). "Диаграммная классификация λ-минимальных решеток Брюа и d-полных множеств". Журнал алгебраической комбинаторики. 9: 61–94. Дои:10.1023 / А: 1018615115006.
- ^ Ким, Чан Су; Ю, Мисью (2019). «Свойство длины крючка d-полных множеств через q-интегралы». Журнал комбинаторной теории, серия A. 162: 167–221. arXiv:1708.09109. Дои:10.1016 / j.jcta.2018.11.003.
внешняя ссылка
- Удивительная математика самых длинных возрастающих подпоследовательностей пользователя Dan Romik. Содержит обсуждение формулы длины крюка и нескольких ее вариантов с приложениями к математике самых длинных возрастающих подпоследовательностей.










































































![{ displaystyle a _ {( lambda _ {1} + k-1, lambda _ {2} + k-2, dots, lambda _ {k})} (x_ {1}, x_ {2}, dots, x_ {k}) = det ! left [{ begin {matrix} x_ {1} ^ {l_ {1}} & x_ {2} ^ {l_ {1}} & dots & x_ {k} ^ {l_ {1}} x_ {1} ^ {l_ {2}} & x_ {2} ^ {l_ {2}} & dots & x_ {k} ^ {l_ {2}} vdots & vdots & ddots & vdots x_ {1} ^ {l_ {k}} & x_ {2} ^ {l_ {k}} & dots & x_ {k} ^ {l_ {k}} конец {матрица}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72f762e80965c37a3dd16c04570af7fb90b402f3)



![left [ Delta (x) p _ {{1 ^ {{(n)}}}} right] _ {{l_ {1}, cdots, l_ {k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ac57aa4ae89fc6f532bc8ce5a090f96254b54488)



![{ frac {n!} {l_ {1}! l_ {2}! cdots l_ {k}!}} sum _ {{w in S_ {n}}} operatorname {sgn} (w) left [(l_ {1}) (l_ {1} -1) cdots (l_ {1} -w (1) +2) right] left [(l_ {2}) (l_ {2} -1 ) cdots (l_ {2} -w (2) +2) right] left [(l_ {k}) (l_ {k} -1) cdots (l_ {k} -w (k) +2 )верно]](https://wikimedia.org/api/rest_v1/media/math/render/svg/14c8d78b31e6e2b9ffe8ae395f6554d0e7d02f5b)
![{ displaystyle det left [{ begin {matrix} 1 & l_ {1} & l_ {1} (l_ {1} -1) & dots & prod _ {i = 0} ^ {k-2} (l_ {1} -i) 1 & l_ {2} & l_ {2} (l_ {2} -1) & dots & prod _ {i = 0} ^ {k-2} (l_ {2} -i) vdots & vdots & vdots & ddots & vdots 1 & l_ {k} & l_ {k} (l_ {k} -1) & dots & prod _ {i = 0} ^ {k- 2} (l_ {k} -i) end {matrix}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c15961bb750a507f64560769201781a3dfd3a9b0)

































