WikiDer > Перевернутый курносый додекадодекаэдр
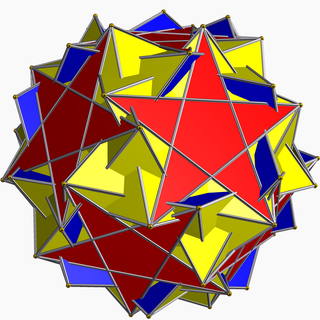
| Перевернутый курносый додекадодекаэдр | |
|---|---|
 | |
| Тип | Равномерный звездный многогранник |
| Элементы | F = 84, E = 150 V = 60 (χ = −6) |
| Лица по сторонам | 60{3}+12{5}+12{5/2} |
| Символ Wythoff | | 5/3 2 5 |
| Группа симметрии | Я, [5,3]+, 532 |
| Указатель ссылок | U60, C76, W114 |
| Двойной многогранник | Средний перевернутый пятиугольный гексеконтаэдр |
| Фигура вершины |  3.3.5.3.5/3 |
| Акроним Bowers | Исдид |
В геометрия, то перевернутый курносый додекадодекаэдр (или же вертиснуб додекадодекаэдр) это невыпуклый однородный многогранник, индексируется как U60.[1] Дается Символ Шлефли ср {5 / 3,5}.
Декартовы координаты
Декартовы координаты для вершин перевернутого курносого додекадодекаэдра являются все даже перестановки из
- (± 2α, ± 2, ± 2β),
- (± (α + β / τ + τ), ± (-ατ + β + 1 / τ), ± (α / τ + βτ-1)),
- (± (-α / τ + βτ + 1), ± (-α + β / τ-τ), ± (ατ + β-1 / τ)),
- (± (-α / τ + βτ-1), ± (α-β / τ-τ), ± (ατ + β + 1 / τ)) и
- (± (α + β / τ-τ), ± (ατ-β + 1 / τ), ± (α / τ + βτ + 1)),
с четным числом плюсов, где
- β = (α2/ τ + τ) / (ατ − 1 / τ),
где τ = (1+√5) / 2 - это Золотая середина а α - отрицательное действительное корень τα4−α3+ 2α2−α − 1 / τ, или приблизительно −0,3352090. нечетные перестановки приведенных выше координат с нечетным числом знаков плюс дает другую форму, энантиоморф другого.
Связанные многогранники
Средний перевернутый пятиугольный гексеконтаэдр
| Средний перевернутый пятиугольный гексеконтаэдр | |
|---|---|
 | |
| Тип | Звездный многогранник |
| Лицо |  |
| Элементы | F = 60, E = 150 V = 84 (χ = −6) |
| Группа симметрии | Я, [5,3]+, 532 |
| Указатель ссылок | DU60 |
| двойственный многогранник | Перевернутый курносый додекадодекаэдр |
В средний перевернутый пятиугольный шестигранник (или же средне-лепестковидный дитриаконтаэдр) невыпуклый равногранный многогранник. Это двойной из униформа перевернутый курносый додекадодекаэдр. Его грани представляют собой неправильные невыпуклые пятиугольники с одним очень острым углом.
Пропорции
Обозначим Золотое сечение к , и разреши - наибольший (наименьший отрицательный) действительный нуль многочлена . Тогда каждая грань имеет три равных угла , один из и один из . Каждая грань имеет одно ребро средней длины, два коротких и два длинных. Если средняя длина , то короткие края имеют длину
- ,
а длинные края имеют длину
- .
В двугранный угол равно . Другой действительный нуль многочлена играет аналогичную роль для средний пятиугольный гексеконтаэдр.
Смотрите также
Рекомендации
- Веннингер, Магнус (1983), Двойные модели, Издательство Кембриджского университета, ISBN 978-0-521-54325-5, МИСТЕР 0730208 п. 124
- ^ Роман, Мэдер. "60: перевернутый курносый додекадодекаэдр". MathConsult.
внешняя ссылка
- Вайсштейн, Эрик В. «Медиальный перевернутый пятиугольный гексеконтаэдр». MathWorld.
- Вайсштейн, Эрик В. «Перевернутый курносый додекадодекаэдр». MathWorld.
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |












