WikiDer > Извлечение изолинии
Извлечение изолинии это дистанционное зондирование обратный метод который извлекает один или несколько изолинии следа атмосферного компонента или переменной. При использовании для проверки другого контура это наиболее точный метод из возможных. При использовании для получения всего поля это общий нелинейный обратный метод и надежная оценка.
Для проверки допустимых контуров
Обоснование
Предположим, у нас есть, как в контурная адвекция, предполагаемое знание единого контура или изолинии атмосферного компонента, qи мы хотим подтвердить это на основе данных спутникового дистанционного зондирования. Поскольку спутниковые инструменты не могут измерять составляющую напрямую, нам необходимо выполнить некоторую инверсию. Для проверки контура нет необходимости знать в любой данной точке, точное значение составляющей. Нам только нужно знать, попадает он внутрь или наружу, то есть больше или меньше значения контура, q0.
Это проблема классификации. Позволять:
- дискретизированная переменная, которая будет связана со спутником вектор измерения, , по некоторой условной вероятности, , который мы аппроксимируем путем сбора выборок, называемых данные обучения, как вектора измерения, так и переменной состояния, q. Путем создания результатов классификации по интересующей области и использования любого алгоритма построения контуров для разделения двух классов изолиния будет «извлечена».
Точность поиска будет определяться интегрированием условной вероятности по интересующей области, А:
куда c - это полученный класс в позиции, .Мы можем максимизировать эту величину, максимизируя значение подынтегральной функции в каждой точке:
Поскольку это определение максимального правдоподобия, a алгоритм классификации на основе максимальная вероятностьявляется наиболее точным из возможных методов проверки проведенного контура. Хорошим методом для выполнения классификации максимального правдоподобия на основе набора обучающих данных является оценка плотности переменного ядра.
Данные обучения
Существует два метода генерации обучающих данных. Самый очевидный из них - эмпирически, просто сопоставляя измерения переменной, q, с совмещенныйизмерения со спутникового прибора. В этом случае не требуется никаких знаний реальной физики, обеспечивающей измерение, и алгоритм поиска является чисто статистическим. Во-вторых, с прямой моделью:
куда это вектор состояния ид = хk является единственным компонентом. Преимущество этого метода заключается в том, что векторы состояния не должны отражать фактические атмосферные конфигурации, они должны только принимать состояние, которое могло бы разумно возникнуть в реальной атмосфере. Также нет ни одной из ошибок, присущих большинству словосочетание процедуры, например из-за ошибок смещения в расположении парных выборок и различий в размерах отпечатков двух приборов. Однако, поскольку извлечение будет смещено в сторону более общих состояний, статистика должна отражать таковые в реальном мире.
Характеристика ошибок
Условные вероятности, , обеспечивают отличную характеристику ошибок, поэтому алгоритм классификации должен их возвращать. рейтинг доверия путем изменения масштаба условной вероятности:
куда пc - количество классов (в данном случае два). C равен нулю, то классификация немного лучше, чем случайность, а если она равна единице, то она должна быть идеальной. Чтобы преобразовать рейтинг достоверности в статистический толерантность, следующий линейный интеграл можно применить к поиску изолинии, истинная изолиния которой известна:
куда s это путь, л - длина изолинии, а - полученная достоверность как функция положения. Хотя кажется, что интеграл должен оцениваться отдельно для каждого значения рейтинга достоверности, C, фактически это может быть одно для всех значений C путем сортировки оценок достоверности результатов, .Функция связывает пороговое значение рейтинга достоверности, для которого применим допуск, то есть определяет область, которая содержит долю истинной изолинии, равную допуску.
Пример: водяной пар из AMSU
В Усовершенствованный прибор для микроволнового зондирования (AMSU) серия спутниковых приборов предназначена для определения температуры и водяного пара. Они имеют высокое разрешение по горизонтали (всего 15 км) и, поскольку они установлены на более чем одном спутнике, полное глобальное покрытие может быть получено менее чем за один день. Данные для обучения были получены с использованием второго метода изЕвропейский центр среднесрочных прогнозов погоды (ECMWF) ERA-40 данные переданы на быстрый перенос излучения модель называетсяРТТОВ.Функция, был сгенерирован из смоделированных выборок и показан на рисунке справа. Затем он используется для установки 90-процентного допуска на рисунке ниже путем затенения всех оценок достоверности менее 0,8. Таким образом, мы ожидаем, что истинная изолиния будет находиться в пределах затененных 90 процентов. времени.
Для непрерывного поиска
Извлечение изолинии также полезно для извлечения переменной континуума и составляет общую, нелинейный обратный метод.Он имеет преимущество перед обоими нейронная сеть, а также итерационные методы, такие как оптимальная оценка которые инвертируют прямую модель, так что нет возможности застрять вместный минимум.
Существует ряд методов восстановления непрерывной переменной из дискретизированной. После получения достаточного количества контуров легко интерполировать между ними. Условные вероятности делают добро доверенное лицо для континуального значения.
Рассмотрим преобразование континуума в дискретную переменную:
Предположим, что дается гауссианом:
куда это математическое ожидание и - стандартное отклонение, то условная вероятность связана с переменной континуума, q, функцией ошибок:
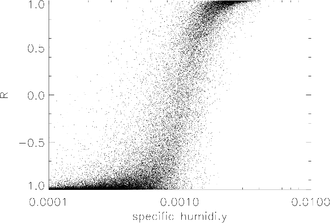
На рисунке показана зависимость условной вероятности от удельной влажности для описанного выше примера извлечения.
Как надежный оценщик
Расположение q0 находится путем установления равных условных вероятностей двух классов:
Другими словами, равные количества «момента нулевого порядка» лежат по обе стороны от q0. Такая формулировка характерна для робастная оценка.
Рекомендации
- Питер Миллс (2009). «Извлечение изолинии: оптимальный метод проверки проведенных контуров» (PDF). Компьютеры и науки о Земле. 35 (11): 2020–2031. arXiv:1202.5659. Bibcode:2009CG ..... 35.2020M. Дои:10.1016 / j.cageo.2008.12.015.
- Питер Миллс (2010). «Эффективная статистическая классификация спутниковых измерений» (PDF). Международный журнал дистанционного зондирования. arXiv:1202.2194. Дои:10.1080/01431161.2010.507795. Архивировано из оригинал (PDF) на 2012-04-26. Получено 2011-12-28.



![{ displaystyle a = { frac {1} {A}} int _ {A} P left [c ({ vec {r}}) | { vec {y}} ({ vec {r} }) right] , d { vec {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c4fa17200419b1532d0eea5b9abaeaaf718cbca)

![{ displaystyle max (a) = { frac {1} {A}} int _ {A} left lbrace max _ {j} P left [j | { vec {y}} ({ vec {r}}) right] right rbrace , d { vec {r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc3f400061e6e717918c8b30adef84493b0099a5)











![{ displaystyle P (q | { vec {y}}) = { frac {1} {{ sqrt {2 pi}} sigma _ {q}}} exp left lbrace - { frac { left [q - { bar {q}} ({ vec {y}}) right] ^ {2}} {2 sigma _ {q}}} right rbrace}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53daae81a91bac5fcd7c03cb02302b03e23b95b1)


![{ Displaystyle R = P (2 | { vec {y}}) - P (1 | { vec {y}}) = mathrm {erf} left [{ frac {q_ {0} - { bar {q}} ({ vec {y}})} {{ sqrt {2}} sigma _ {q}}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/379ebd5c9b5f457ac3737292ffacc26622d54f04)
