WikiDer > График Джонсона - Википедия
| Граф Джонсона | |
|---|---|
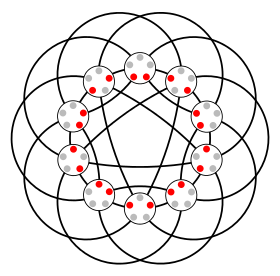 Граф Джонсона J(5,2) | |
| Названный в честь | Селмер М. Джонсон |
| Вершины | |
| Края | |
| Диаметр | |
| Характеристики | -обычный Вершинно-транзитивный Дистанционно-транзитивный Гамильтон-связанный |
| Обозначение | |
| Таблица графиков и параметров | |
Графики Джонсона особый класс неориентированные графы определяется из систем множеств. Вершины графа Джонсона являются -элементные подмножества -комплект элементов; две вершины смежны, если пересечение двух вершин (подмножеств) содержит -элементы.[1] И графы Джонсона, и тесно связанные с ними Схема Джонсона названы в честь Селмер М. Джонсон.
Особые случаи
- это полный график Kп.
- это октаэдрический граф.
- это дополнительный граф из Граф Петерсена,[1] следовательно линейный график из K5. В общем, для всех , граф Джонсона является дополнением к Граф Кнезера
Теоретико-графические свойства
- изоморфен
- Для всех , любая пара вершин на расстоянии Поделиться общие элементы.
- является Гамильтон-связанный, что означает, что каждая пара вершин образует концы Гамильтонов путь в графике. В частности, это означает, что он имеет гамильтонов цикл.[2]
- Также известно, что граф Джонсона является-вершинно-связанные.[3]
- образует граф вершин и ребер (п - 1) -мерный многогранник, называется гиперсимплекс.[4]
- то номер клики из дается выражением через его наименьшее и наибольшее собственные значения:
- В хроматическое число из самое большее [5]
Группа автоморфизмов
Существует дистанционно-переходный подгруппа изоморфен . Фактически, , пока не ; иначе, .[6]
Массив пересечений
Как следствие того, что они дистанционно транзитивны, это также дистанционно-регулярный. Сдача обозначим его диаметр, массив пересечений дан кем-то
куда:
Оказывается, если является , его массив пересечений не используется совместно с каким-либо другим дистанционно регулярным графом; массив пересечений разделяется с тремя другими дистанционно регулярными графами, которые не являются графами Джонсона.[1]
Собственные значения и собственные векторы
- Характеристический многочлен дан кем-то
- куда [6]
- Собственные векторы иметь четкое описание.[7]
Схема Джонсона
Граф Джонсона тесно связан с Схема Джонсона, схема ассоциации в котором каждая пара k-элементный набор связан с числом, половиной размера симметричная разница из двух наборов.[8] Граф Джонсона имеет ребро для каждой пары множеств на расстоянии один в схеме ассоциации, и расстояния в схеме ассоциации в точности равны кратчайший путь расстояния в графе Джонсона.[9]
Схема Джонсона также связана с другим семейством дистанционно-транзитивных графов, нечетные графики, вершины которого -элементные подмножества -элементное множество, ребра которого соответствуют непересекающимся парам подмножеств.[8]
Открытые проблемы
Свойства расширения вершин графов Джонсона, а также структура соответствующих экстремальных множеств вершин заданного размера до конца не изучены. Однако недавно была получена асимптотически точная нижняя оценка разложения больших множеств вершин.[10]
В общем, определение хроматического числа графа Джонсона - открытая проблема.[11]
Смотрите также
Рекомендации
- ^ а б c Холтон, Д. А .; Шихан, Дж. (1993), «Графики Джонсона и даже графики», Граф Петерсена, Серия лекций Австралийского математического общества, 7, Кембридж: Издательство Кембриджского университета, стр. 300, Дои:10.1017 / CBO9780511662058, ISBN 0-521-43594-3, МИСТЕР 1232658.
- ^ Альспах, Брайан (2013), «Графы Джонсона гамильтоновы связны», Ars Mathematica Contemporanea, 6 (1): 21–23, Дои:10.26493/1855-3974.291.574.
- ^ Ньюман, Илан; Рабинович, Юрий (2015), О связности фасетных графов симплициальных комплексов, arXiv:1502.02232, Bibcode:2015arXiv150202232N.
- ^ Рисполи, Фред Дж. (2008), График гиперсимплекса, arXiv:0811.2981, Bibcode:2008arXiv0811.2981R.
- ^ "Джонсон". www.win.tue.nl. Получено 2017-07-26.
- ^ а б Э., Брауэр, Андрис (1989). Дистанционно-регулярные графики. Коэн, Арджех М., Ноймайер, Арнольд. Берлин, Гейдельберг: Springer Berlin Heidelberg. ISBN 9783642743436. OCLC 851840609.
- ^ Фильмус, Юваль (2014), Ортогональный базис для функций над срезом булевого гиперкуба, arXiv:1406.0142, Bibcode:2014arXiv1406.0142F.
- ^ а б Кэмерон, Питер Дж. (1999), Группы перестановок, Студенческие тексты Лондонского математического общества, 45, Cambridge University Press, стр. 95, ISBN 9780521653787.
- ^ Таким образом, явное отождествление графов со схемами ассоциации можно увидеть в Боз, Р. К. (1963), "Сильно регулярные графы, частичные геометрии и частично сбалансированные планы", Тихоокеанский математический журнал, 13 (2): 389–419, Дои:10.2140 / pjm.1963.13.389, МИСТЕР 0157909.
- ^ Христофидес, Деметрес; Эллис, Дэвид; Кееваш, Питер (2013), "Приближенное вершинно-изопериметрическое неравенство для $ r $ -множеств", Электронный журнал комбинаторики, 4 (20).
- ^ 1949-, Годсил, К. Д. (Кристофер Дэвид) (2016). Теоремы Эрдеша-Ко-Радо: алгебраические подходы. Мигер, Карен (учитель колледжа). Кембридж, Соединенное Королевство. ISBN 9781107128446. OCLC 935456305.CS1 maint: числовые имена: список авторов (связь)
































