WikiDer > Калейдоцикл
| Правые пирамиды с регулярным основанием | |
|---|---|
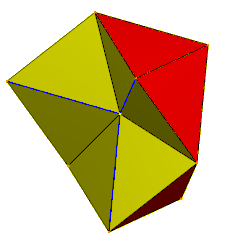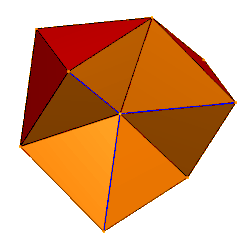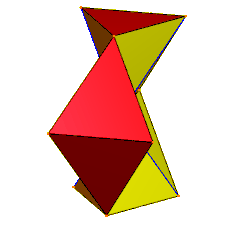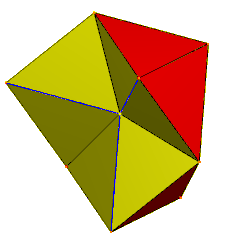 6 тетраэдров, вершины которых пересекаются в центре. Синие края дублируются, пары лиц скрыты. | |
| Лица | 24 равнобедренные треугольники |
| Края | 36 (6 как вырожденные пары) |
| Вершины | 12 |
| Группа симметрии | C3v, [3], (* 33), порядок 6 |
| Характеристики | тор |
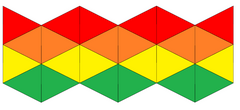 Сеть | |

А калейдоцикл (или же флекстангл) представляет собой сложенную из бумаги модель, соединяющую 6 тетраэдры (или же дисфеноиды) на противоположных сторонах в цикл. Если грани дифеноидов представляют собой равносторонние треугольники, Его можно построить из растянутого треугольная черепица сетка с 4-мя треугольниками в одном направлении и четным числом в другом.
Модель представляет собой гибкий многогранник (с вырожденными парами совпадающих ребер в переходе), которые можно скручивать вокруг оси кольца, показывая 4 набора из 6 треугольных граней, которые можно нарисовать разными цветами или узорами.
Пример
Калейдоцикл с использованием дисфеноидов с разносторонними треугольными гранями. Каждый шарнир соединяет дисфеноид с его хиральный партнер. Соответствующая сеть следовательно, проявляет отражательную симметрию.
Вариации
Помимо 6 сторон, большее четное количество тетраэдров, 8, 10, 12 и т. Д., Могут быть соединены вместе. Эти модели оставляют центральный зазор, в зависимости от пропорций граней треугольника.[1]
История
Уоллес Уокер придумал слово калейдоцикл в 1950-х из греческого калос (красивая), эйдос (форма) и Киклос (звенеть).
В 1977 г. Дорис Шатчнайдер а Уоллес Уокер опубликовал книгу о них, используя M.C. Эшер узоры.[2][3]
Культурное использование
Это называлось флекстангл в качестве реквизита в фильме 2018 года Морщинка во времени, с его внутренними гранями, раскрашенными сердечками и узорами, которые скрыты, когда сложенный вместе. Бумажная игрушка подсказывала, как можно сложить пространство и время, чтобы объяснить волшебные путешествия этой истории. Игрушка дарит дочери ее отец в начале фильма, и ее сердца показывают, насколько может быть любовь. завернутый и все еще там, даже после того, как отец загадочным образом исчез.[4]
Смотрите также
Рекомендации
- ^ решения правильных тетраэдров, 8, 10, 12 с Mathematica
- ^ Рецензия на книгу: искусство встречает математику в "калейдоциклах" 27 мая 1988 г.
- ^ Дорис Шатчнайдер и Уокер, M.C. Эшер Калейдоциклы, 1977. ISBN 0-906212-28-6. [1]
- ^ Купер, Меган (8 марта 2018 г.). «Дисней Морщинка во времени, калейдоцикл, флекстангл и задания для печати». Jamonkey. Получено 15 октября, 2018.
внешняя ссылка
- Калейдоциклы: удивительные динамические поделки из бумаги
- Как сделать калейдоцикл
- Калейдоциклы
- Калейдоцикл: 7 шагов (с изображениями) - инструкции
- Калейдоциклы сетевым методом
- Бесплатная печать Хэллоуина Flextangle (Kaleidocycle)
- Калейдоциклы
- Создатель флекстангл онлайн
- Калейдоциклы с 6 дисфеноидами
| Этот многогранник-связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
