WikiDer > Графики Клейна
в математический поле теория графов, то Графики Клейна два разных, но связанных регулярные графики, каждая по 84 ребра. Каждый может быть вложен в ориентируемый поверхность из род 3, в котором они образуют двойственные графы.
Кубический граф Клейна
| (Кубический) граф Клейна | |
|---|---|
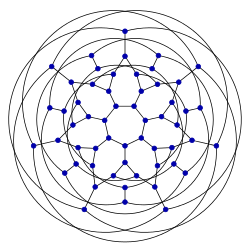 Граф 56-Клейна | |
| Названный в честь | Феликс Кляйн |
| Вершины | 56 |
| Края | 84 |
| Радиус | 6 |
| Диаметр | 6 |
| Обхват | 7 |
| Автоморфизмы | 336 |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Симметричный Кубический Гамильтониан Граф Кэли |
| Таблица графиков и параметров | |
Этот график представляет собой 3-регулярный график с 56 вершинами и 84 ребрами, названные в честь Феликс Кляйн.
Это Гамильтонов граф. Она имеет хроматическое число 3, хроматический индекс 3, радиус 6, диаметр 6 и обхват 7. Это также 3-вершинно-связанный и 3-реберный график. Она имеет толщина книги 3 и номер очереди 2.[1]
Его можно встроить в род-3 ориентируемые поверхность (который можно представить как Кляйн квартика), где он образует «карту Клейна» с 24 семиугольными гранями, Символ Шлефли {7,3}8.
Согласно Приемная перепись, граф Клейна, обозначаемый как F056B, является единственным кубическим симметричным графом с 56 вершинами, который не является двудольный.[2]
Его можно вывести из 28-вершинного Граф Кокстера.[3]
Алгебраические свойства
Группа автоморфизмов графа Клейна - это группа PGL2(7) заказа 336, в которомPSL2(7) как нормальная подгруппа. Эта группа действует транзитивно на своих полуребрах, поэтому граф Клейна является симметричный граф.
В характеристический многочлен этого 56-вершинного графа Клейна равно
Галерея
Альтернативный рисунок кубического графа Клейна, показывающий, что он гамильтонов, с хроматический индекс 3.
7-валентный граф Клейна
| (7-валентный) граф Клейна | |
|---|---|
 Граф 24-Клейна | |
| Названный в честь | Феликс Кляйн |
| Вершины | 24 |
| Края | 84 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 3 |
| Автоморфизмы | 336 |
| Хроматическое число | 4 |
| Хроматический индекс | 7 |
| Характеристики | Симметричный Гамильтониан |
| Таблица графиков и параметров | |
Этот график представляет собой 7-регулярный график с 24 вершинами и 84 ребрами, названные в честь Феликс Кляйн.
Это Гамильтонов граф. Она имеет хроматическое число 4, хроматический индекс 7, радиус 3, диаметр 3 и обхват 3.
Он может быть вложен в ориентируемую поверхность рода 3, где он образует двойственную «карту Клейна» с 56 треугольными гранями, Символ Шлефли {3,7}8.[4]
Это уникальный дистанционно регулярный граф с массивом пересечений ; однако это не дистанционно-транзитивный граф.[5]
Алгебраические свойства
Группа автоморфизмов 7-валентного графа Клейна - это та же группа порядка 336, что и для кубического отображения Клейна, аналогичным образом действующая транзитивно на его полуребрах.
В характеристический многочлен этого 24-вершинного графа Клейна равно .[6]
Рекомендации
- ^ Вольц, Джессика; Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Кондер, М.; Добчаньи, П. (2002), "Трехвалентные симметрические графы до 768 вершин", J. Combin. Математика. Комбинировать. Comput., 40: 41–63.
- ^ Дейтер, Итало. «От графа Кокстера к графу Клейна». CiteSeer. CiteSeerX 10.1.1.188.2580. Цитировать журнал требует
| журнал =(помощь) - ^ Шульте, Эгон; Уиллс, Дж. М. (1985). "Многогранная реализация карты Феликса Клейна {3, 7}8 на римановой поверхности рода 3 ". J. London Math. Soc. s2-32 (3): 539–547. Дои:10.1112 / jlms / s2-32.3.539.
- ^ Брауэр, Андрис; Коэн, Арджех; Ноймайер, Арнольд (1989). Дистанционно-регулярные графики. Springer-Verlag. п.386. ISBN 978-0-387-50619-7.
- ^ van Dam, E. R .; Haemers, W. H .; Koolen, J. H .; Спенс Э. (2006). «Характеризация дистанционно-регулярности графиков спектром». J. Combin. Теория Сер. А. 113 (8): 1805–1820. Дои:10.1016 / j.jcta.2006.03.008.




