WikiDer > Теорема Коснитаса - Википедия
В Евклидова геометрия, Теорема Косницы является собственностью определенных круги связанный с произвольным треугольник.
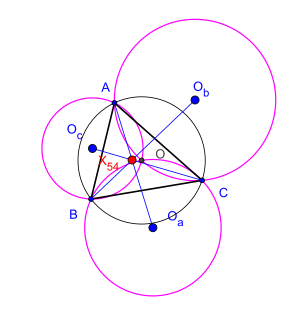
Позволять - произвольный треугольник, это центр окружности и центры окружности трех треугольников , , и соответственно. Теорема утверждает, что три прямые линии , , и совпадают.[1] Этот результат был установлен румынским математиком. Цезарь Кошницэ (1910-1962).[2]
Их точка совпадения известна как точка треугольника. Косница точка (названный Ригби в 1997 году). Это изогональный конъюгат из центр девяти точек.[3][4] это центр треугольника в Список Кларка Кимберлинга.[5] Эта теорема является частным случаем Теорема Дао о шести центрах окружности связанный с циклическим шестиугольником в.[6][7][8][9][10][11][12]
Рекомендации
- ^ Вайсштейн, Эрик В. "Теорема Косницы". MathWorld.
- ^ Ион Пэтрашку (2010), Обобщение теоремы Косницы (на румынском)
- ^ Дарий Гринберг (2003), О точке Косница и отражающем треугольнике. Форум Геометрикорум, том 3, страницы 105–111. ISSN 1534-1178
- ^ Джон Ригби (1997), Краткие заметки о некоторых забытых геометрических теоремах. Mathematics and Informatics Quarterly, том 7, страницы 156–158 (цитируется Кимберлингом).
- ^ Кларк Кимберлинг (2014), Энциклопедия центров треугольников В архиве 2012-04-19 в Wayback Machine, раздел X (54) = Мыс Косница. Дата обращения 2014-10-08.
- ^ Николаос Дергиадес (2014), Теорема Дао о шести круговых центрах, связанных с циклическим шестиугольником. Форум Геометрикорум, том 14, стр. = 243–246. ISSN 1534-1178.
- ^ Телв Кол (2014), Чисто синтетическое доказательство теоремы Дао о шести центрах окружности, связанных с циклическим шестиугольником. Форум Геометрикорум, том 14, страницы 261–264. ISSN 1534-1178.
- ^ Нго Куанг Зыонг, Международный журнал компьютерной математики, Некоторые проблемы вокруг теоремы Дао о шести центрах окружности, связанные с конфигурацией циклического шестиугольника, том 1, страницы = 25-39. ISSN 2367-7775
- ^ Кларк Кимберлинг (2014), X (3649) = KS (ИНТУАЛЬНЫЙ ТРЕУГОЛЬНИК)
- ^ Нгуен Минь Ха, Еще одно чисто синтетическое доказательство теоремы Дао о шести круговых центрах. Журнал перспективных исследований классической и современной геометрии, ISSN 2284-5569, том 6, страницы 37–44. МИСТЕР....
- ^ Нгуен Тьён Донг, Простое доказательство теоремы Дао о шести круговых центрах. Журнал перспективных исследований классической и современной геометрии, ISSN 2284-5569, том 6, страницы 58–61. МИСТЕР....
- ^ Продолжение круга до коники с центром: творческий метод новых теорем, Международный журнал компьютерной математики, стр.21-32.