WikiDer > Лестничный график
| Лестничный график | |
|---|---|
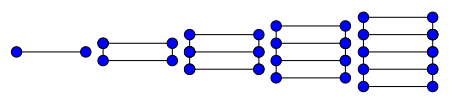
 Лестничный график L8. | |
| Вершины | 2n |
| Края | 3н-2 |
| Хроматическое число | 2 |
| Хроматический индекс | 3 для п> 2 2 для п = 2 1 для п = 1 |
| Свойства | Единичное расстояние Гамильтониан Планарный Двудольный |
| Обозначение | Lп |
| Таблица графиков и параметров | |
в математический поле теория графов, то лестничный график Lп это планарный неориентированный граф с участием 2n вершины и 3н-2 края.[1]
Лестничный график можно получить как Декартово произведение из двух графы путей, у одного из которых только одно ребро: Lп,1 = пп × п2.[2][3]
Свойства
По построению лестничный граф Lп изоморфен сетка графика г2,п и выглядит как лестница с п ступеньки. это Гамильтониан с обхватом 4 (если п> 1) и хроматический индекс 3 (если п> 2).
В хроматическое число лестничного графа равно 2, а его хроматический полином является .
В хроматическое число лестничного графа равно 2.
Лестничный график
Иногда термин «лестничный график» используется для обозначения п × п2 лестничный график, который является объединением графов п копии графа путей P2.
Круговой лестничный график
В круговой лестничный график CLп можно построить, соединив четыре вершины 2-степени в Прямо способом, или декартовым произведением цикла длины n≥3 и край.[4]В символах CLп = Cп × п2. Она имеет 2n узлы и 3n рёбер.Как и лестничный граф, это связанный, планарный и Гамильтониан, но это двудольный если и только если п даже.
Круговой лестничный график - это многогранные графы призм, поэтому их чаще называют призматические графики.
Круговые лестничные диаграммы:
 CL3 |  CL4 |  CL5 |  CL6 |  CL7 |  CL8 |
Лестница Мебиуса
Соединение четырех вершин 2 степени поперек создает кубический граф называется лестницей Мёбиуса.
использованная литература
- ^ Вайсштейн, Эрик В. «Лестничный график». MathWorld.
- ^ Хосоя, Х. и Харари, Ф. «О совпадающих свойствах трех графов заборов». J. Math. Chem. 12, 211-218, 1993.
- ^ Ной М. и Рибо А. "Рекурсивно конструируемые семейства графов". Adv. Appl. Математика. 32, 350-363, 2004.
- ^ Чен, Ичао; Гросс, Джонатан Л .; Мансур, Туфик (сентябрь 2013 г.). «Распределения полного погружения круговых лестниц». Журнал теории графов. 74 (1): 32–57. CiteSeerX 10.1.1.297.2183. Дои:10.1002 / jgt.21690.