WikiDer > Линии действия - Википедия

Направления действий
	Исходное положение линий действия
Дизайнер (ы)	Клод Суси
Жанр (ы)	Настольная игра ; Абстрактная стратегическая игра
Игроки	2
Время установки	<1 минута
Случайный шанс	Никто
Требуются навыки	Стратегия, тактика
Синоним (ы)	LOA

Lines of Action - Wikipedia

Направления действий (или же LOA) является абстрактная стратегия настольная игра для двух игроков изобрел Клод Суси. Цель состоит в том, чтобы соединять все части в единую группу.

Игра была рекомендована Spiel des Jahres в 1988 г.^[1]

Правила

Цель

Цель игры - собрать все свои шашки в единое целое так, чтобы они были соединены по вертикали, горизонтали или диагонали (8-подключение).^{[требуется разъяснение]}

Сводка движения

Игроки чередуют ходы, причем у черных первый ход.
Шашки перемещаются по горизонтали, вертикали или диагонали.
Шашка перемещается ровно на столько клеток, сколько шашек (как своих, так и вражеских) на линии, по которой она движется. Например, черные могут начать c8-c6. Вторая шашка черных

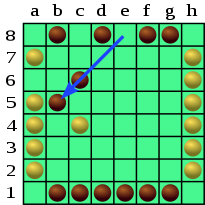
Диаграммы движения

Шашка не может перепрыгивать через шашку противника. Таким образом, на диаграмме ниже белые не могут сыграть a6-d6, даже если в ряду 6 три шашки. Вместо этого белые могут сыграть a6-c4, сделав два шага, потому что на диагонали (a6-f1) две шашки, в которых белые движется.

Шашка может перепрыгивать дружеские шашки. Таким образом, черные могут продолжить ход e8-b5, прыгая в свою шашку. Он перемещается на три клетки, потому что на диагонали (a4-e8), по которой он движется, стоят три шашки.

Шашка может приземлиться на поле, занятое шашкой противника, в результате чего последняя будет взята и удалена из игры. Например, белые могут сыграть h3-f1, захватив черную шашку на f1.

Игрок, сведенный к одной шашке, побеждает в игре, потому что его фишки по определению объединены. Если в результате взятия ход приводит к тому, что каждый игрок имеет все свои фишки в одном теле, то выигрывает либо игрок, который движется, или игра является ничьей, в зависимости от правил, действующих на конкретном турнире.

Одновременное подключение

В оригинальном издании «Gamut of Games» 1969 года одновременное подключение описывалось как ничья. Во втором издании правила были изменены, чтобы объявить это победой для игрока. Вот примечание Сида Саксона в предисловии ко второму изданию: «Клод Суси и я - все, что осталось от N.Y.G.A. По его просьбе я исправил ошибку в правилах для ЛИНИЙ ДЕЙСТВИЙ, исключив возможные ничьи». Однако, несмотря на намерение изобретателя LOA, большинство современных турниров, включая чемпионаты мира, Олимпиада интеллектуального спорта засчитать одновременное подключение вничью.

Стратегия

Игра может стать довольно тактической на открытых позициях, где шашки с обеих сторон мобильны. Однако стратегическая глубина игры во многом определяется стратегиями блокирования, разработанными для ограничения мобильности противника. Может быть выгодно прикрепить одну или несколько вражеских шашек к краю доски, переместившись во второй ряд или столбец.

Наличие большего количества шашек обычно является преимуществом, потому что они могут ограничивать возможности оппонента по мере того, как они объединяются. С другой стороны, материальные соображения не так важны, потому что меньшее количество шашек также означает меньше возможностей для объединения.

Пример игры

Вышеупомянутые ходы иллюстрируют правила, но не обязательно хорошую игру. Следующие ходы более типичны для экспертной игры.

Черные играют b1-b3. Шашка перемещает два квадрата по вертикали, потому что в файле две шашки: b1 и b8. Этот ход не дает белым возможности взять и угрожает зажать фигуры на вертикали.

Белые ходят h4-f2. Шашка перемещается на две клетки, потому что по диагонали две шашки: h4 и e1. Белые угрожают подвижности шашек черных в нижнем ряду.

Черные играют d1: a4, перепрыгивая через свою шашку (что разрешено) и захватывая белую шашку на a4. Обратите внимание, что черные сделали три клетки, так как по диагонали было три шашки: a4, b3 и d1.

Пока не ясно, выгоден захват или нет. У черных теперь есть дополнительная шашка, но этот ход не сильно помог белым заблокировать или создать центральную массу для черных. Обычно ранние захваты на краю не особенно эффективны, тогда как ранние захваты в центре очень хороши.

Белые играют h2-e2, продолжая блокаду первой горизонтали. Шашка перемещается на три клетки, перепрыгивая через дружескую шашку. Белые, несмотря на существенный недостаток второго хода, очевидно, сейчас лидируют из-за ограниченной подвижности черных шашек первого ряда. Вскоре белые сыграют a2-d2, продолжая строить собственный мост и заставляя черную шашку на e1 двигаться боком, если они хотят присоединиться к игре. Черным вряд ли удастся уйти ходом e1-c3, потому что это позволяет белым взять ход a5: c3.

Пример выигрышного хода

На диаграмме ниже белые сделали ход, который соединяет все их фигуры, в то время как у черных еще не менее двух ходов от такого состояния. Таким образом, белые выиграли партию.