WikiDer > Теорема Лохсса - Википедия
В теория чисел, Теорема Лохса это теорема о скорости сходимости непрерывная дробь расширение типичного действительного числа. Доказательство теоремы опубликовал Густав Лохс в 1964 г.[1]
Теорема утверждает, что для почти все действительные числа в интервале (0,1), количество членов м раскрытия непрерывной дроби числа, которые необходимы для определения первого п места десятичного разложения числа ведет себя асимптотически следующее:
Поскольку этот предел лишь немного меньше 1, это можно интерпретировать как утверждение, что каждый дополнительный член в представлении непрерывной дроби «типичного» действительного числа увеличивает точность представления примерно на один десятичный разряд. В десятичный система последняя позиционная система для которых каждая цифра несет меньше информации, чем одно частное непрерывной дроби; собирается база-11 (изменение к в уравнении) делает указанное выше значение больше 1.
Величина, обратная этому пределу,
является дважды десятичным логарифмом Постоянная Леви.
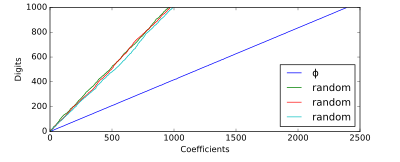
Ярким примером числа, не демонстрирующего такого поведения, является Золотое сечение- иногда известный как "самый иррациональный"число, в котором все члены непрерывной дроби представляют собой единицы, наименьшее возможное в канонической форме. В среднем требуется приблизительно 2,39 членов непрерывной дроби на одну десятичную цифру.[3]
Рекомендации
- ^ Лохс, Густав (1964), "Vergleich der Genauigkeit von Dezimalbruch und Kettenbruch", Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg (на немецком), 27: 142–144, Дои:10.1007 / BF02993063, МИСТЕР 0162753
- ^ Вайсштейн, Эрик В. «Теорема Лохса». MathWorld.
- ^ Купер, Гарольд. «Непрерывные потоки фракций». Получено 30 августа 2016.



