WikiDer > Люнебургская линза
А Люнебургская линза (изначально Lüобъектив Небург, часто неправильно пишется Лунебеобъектив rg) является сферически симметричным линза с градиентным индексом. Показатель преломления типичной линзы Люнебурга п уменьшается радиально от центра к внешней поверхности. Их можно использовать с электромагнитное излучение из видимый свет к радиоволны.
Для определенных профилей индекса линза будет иметь идеальную геометрическую форму. картинки двух данных концентрических сфер друг на друга. Существует бесконечное количество профилей показателя преломления, которые могут вызвать этот эффект. Простейшее такое решение было предложено Рудольф Люнебург в 1944 г.[1] Решение Люнебурга для показателя преломления создает два сопряженных фокусы вне объектива. Решение принимает простой и явный вид, если координационный центр лежит на бесконечности, а другой - на противоположной поверхности линзы. Дж. Браун и А.С. Гутман впоследствии предложили решения, которые создают одну внутреннюю и одну внешнюю фокусные точки.[2][3] Эти решения не уникальны; множество решений определяется набором определенные интегралы которые необходимо оценивать численно.[4]
Дизайн
Люнебургское решение
Каждая точка на поверхности идеальной линзы Люнебурга является фокусом для параллельного излучения, падающего на противоположную сторону. В идеале диэлектрическая постоянная материала линзы падает с 2 в центре до 1 на поверхности (или, что эквивалентно, показатель преломления падает с к 1), согласно
где - радиус линзы. Поскольку показатель преломления на поверхности такой же, как и у окружающей среды, отражение от поверхности не происходит. Внутри линзы траектории лучей представляют собой дуги эллипсы.
Линза Максвелла рыбий глаз
Линза Максвелла «рыбий глаз» также является примером обобщенной линзы Люнебурга. Рыбий глаз, впервые полностью описанный Максвелл в 1854 г.[5] (и, следовательно, предшествует решению Люнебурга), имеет показатель преломления, изменяющийся в зависимости от
Он фокусирует каждую точку на сферической поверхности радиуса р в противоположную точку на той же поверхности. Траектории лучей внутри линзы представляют собой дуги окружностей.
Публикация и атрибуция
Свойства этого объектива описаны в одной из множества задач или головоломок, поставленных в 1853 году. Кембриджский и Дублинский математический журнал.[6] Задача состоит в том, чтобы найти показатель преломления как функцию радиуса, учитывая, что луч описывает круговой путь, и, кроме того, доказать фокусирующие свойства линзы. Решение дано в выпуске 1854 года того же журнала.[5] Проблемы и решения изначально публиковались анонимно, но решение этой (и еще одной) проблемы было включено в Niven's Научные статьи Джеймса Клерка Максвелла,[7] который был опубликован через 11 лет после смерти Максвелла.
Приложения
На практике линзы Люнебурга обычно представляют собой слоистые структуры из дискретных концентрических оболочек, каждая из которых имеет свой показатель преломления. Эти оболочки образуют ступенчатый профиль показателя преломления, который несколько отличается от решения Люнебурга. Этот вид линз обычно используется для микроволновые частоты, особенно для построения эффективных микроволновые антенны и радар калибровочные стандарты. Цилиндрические аналоги линзы Люнебурга также используются для коллимирующий свет от лазерные диоды.
Отражатель радара
А отражатель радара можно сделать из линзы Люнебурга путем металлизации частей ее поверхности. Излучение от дальнего радиолокационного передатчика фокусируется на нижней стороне металлизации на противоположной стороне линзы; здесь он отражается и снова фокусируется на радиолокационной станции. Сложность этой схемы заключается в том, что металлизированные области блокируют вход или выход излучения на этой части линзы, но неметаллизированные области приводят к появлению слепых зон на противоположной стороне.
СВЧ антенна
Линза Люнебурга может быть использована как основа радиоантенны с большим усилением. Эта антенна сопоставима с тарелочная антенна, но в качестве основного фокусирующего элемента использует линзу, а не параболический отражатель. Как и в случае с тарелочной антенной, подача к приемнику или от передатчика помещается в фокус, питание обычно состоит из рупорная антенна. В фазовый центр из кормить рог должен совпадать с точкой фокусировки, но поскольку фазовый центр неизменно находится в некоторой степени внутри устья рупора, его нельзя поднести прямо к поверхности линзы. Следовательно, необходимо использовать различные линзы Люнебурга, которые фокусируются несколько за пределами своей поверхности,[8] а не классический объектив с фокусом на поверхности.
Линзовая антенна Люнебурга имеет ряд преимуществ по сравнению с параболической антенной. Поскольку линза сферически симметрична, антенну можно направлять, перемещая облучатель вокруг линзы, без необходимости поворачивать всю антенну. Опять же, поскольку линза сферически симметрична, одну линзу можно использовать с несколькими лучами, смотрящими в самых разных направлениях. Напротив, если с параболическим отражателем используется несколько источников питания, все они должны находиться в пределах небольшого угла от оптическая ось чтобы избежать страданий кома (форма расфокусировки). Помимо смещение В системах параболические антенны страдают от фидерной и поддерживающей ее конструкции, частично закрывающей основной элемент (закупорка апертуры); как и другие преломляющие системы, линзовая антенна Люнебурга позволяет избежать этой проблемы.
Разновидностью линзовой антенны Люнебурга является полусферическая линзовая антенна Люнебурга или Люнебургская рефлекторная антенна. Здесь используется только одна полусфера линзы Люнебурга, при этом поверхность среза сферы опирается на отражающий металл. плоскость земли. Такое расположение уменьшает вдвое вес линзы, а заземляющая поверхность обеспечивает удобную опору. Однако подача частично закрывает объектив, когда угол падения на отражателе менее 45 °.
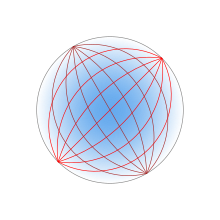
Путь луча внутри линзы
Для любой сферически-симметричной линзы каждый луч целиком лежит в плоскости, проходящей через центр линзы. Начальное направление луча определяет линию, которая вместе с центральной точкой линзы определяет плоскость, разделяющую линзу пополам. Являясь плоскостью симметрии линзы, градиент показателя преломления не имеет компонента, перпендикулярного этой плоскости, который заставлял бы луч отклоняться либо в одну сторону от нее, либо в другую. В самолете круговая симметрия системы позволяет удобно пользоваться полярные координаты для описания траектории луча.
Учитывая любые две точки на луче (например, точку входа и выхода из линзы), Принцип Ферма утверждает, что путь, который луч проходит между ними, - это тот путь, который он может пройти за наименьшее возможное время. Учитывая, что скорость света в любой точке линзы обратно пропорциональна показателю преломления, и Пифагор, время перехода между двумя точками и является
где это скорость света в вакууме. Сведение к минимуму этого дает второй порядок дифференциальное уравнение определение зависимости на по пути луча. Этот тип задач минимизации широко изучался в Лагранжева механика, а готовое решение существует в виде Белтрами личность, который немедленно поставляет первый интеграл этого уравнения второго порядка. Подстановка (где представляет собой ), в это тождество дает
где это постоянная интеграции. Это дифференциальное уравнение первого порядка имеет вид отделяемый, то есть его можно перестроить так, чтобы появляется только с одной стороны, и только с другой:[1]
Параметр является константой для любого данного луча, но отличается для лучей, проходящих на разных расстояниях от центра линзы. Для лучей, проходящих через центр, он равен нулю. В некоторых особых случаях, например, для рыбьего глаза Максвелла, это уравнение первого порядка может быть дополнительно интегрировано, чтобы получить формулу для как функция или . В целом он обеспечивает относительные скорости изменения и , который может быть численно интегрированный чтобы проследить путь луча через линзу.
Смотрите также
- Спутник BLITS (Ball Lens In The Space)
- Гравитационные линзы также имеют уменьшающийся в радиальном направлении показатель преломления.
использованная литература
- ^ а б Люнебург, Р.К. (1944). Математическая теория оптики. Провиденс, Род-Айленд: Брауновский университет. С. 189–213.
- ^ Браун, Дж. (1953). Беспроводной инженер. 30: 250. Отсутствует или пусто
| название =(Помогите) - ^ Гутман, А. С. (1954). «Модифицированная линза Люнеберга». J. Appl. Phys. 25 (7): 855–859. Bibcode:1954JAP .... 25..855G. Дои:10.1063/1.1721757.
- ^ Морган, С. П. (1958). «Общее решение проблемы линзы Люнебурга». J. Appl. Phys. 29 (9): 1358–1368. Bibcode:1958JAP .... 29.1358M. Дои:10.1063/1.1723441. S2CID 119949981.
- ^ а б «Решения проблем (проблема 3, т. VIII. С. 188)». Кембриджский и Дублинский математический журнал. Макмиллан. 9: 9–11. 1854.
- ^ «Проблемы (3)». Кембриджский и Дублинский математический журнал. Макмиллан. 8: 188. 1853.
- ^ Нивен, изд. (1890). Научные статьи Джеймса Клерка Максвелла. Нью-Йорк: Dover Publications. п. 76.
- ^ Lo, Y. T .; Ли, С. В. (1993). Справочник по антеннам: теория антенн. Справочник по антеннам. Springer. п. 40. ISBN 9780442015930.