WikiDer > Последовательность максимальной длины

Maximum length sequence

А последовательность максимальной длины (MLS) является разновидностью псевдослучайная двоичная последовательность.

Это битовые последовательности, созданные с использованием максимального регистры сдвига с линейной обратной связью и называются так потому, что они периодический и воспроизвести каждый двоичная последовательность (кроме нулевого вектора), который может быть представлен регистрами сдвига (т.е.для длиным регистров они производят последовательность длиной 2^м - 1). MLS также иногда называют n-последовательность или m-последовательность. MLS спектрально плоский, за исключением почти нулевого члена постоянного тока.

Эти последовательности могут быть представлены как коэффициенты неприводимых многочленов от кольцо многочленов над Z / 2Z.

Практическое применение MLS включает измерение импульсные реакции (например, комнаты реверберация). Они также используются в качестве основы для получения псевдослучайных последовательностей в цифровых системах связи, которые используют расширенный спектр прямой последовательности и расширенный спектр со скачкообразной перестройкой частоты системы передачи, конструкция оптического диэлектрического многослойного отражателя,^[1] и в эффективном дизайне некоторых фМРТ эксперименты.^[2]

Поколение

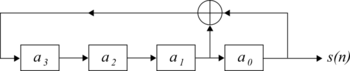
Рисунок 1: Следующее значение регистра а₃ в регистре сдвига с обратной связью длиной 4 определяется суммой по модулю 2 а₀ и а₁.

MLS генерируются с использованием регистров сдвига с максимальной линейной обратной связью. Система, генерирующая MLS со сдвиговым регистром длины 4, показана на рис. 1. Это можно выразить с помощью следующего рекурсивного соотношения:

{ displaystyle { begin {cases} a_ {3} [n + 1] = a_ {0} [n] + a_ {1} [n] a_ {2} [n + 1] = a_ {3} [n] a_ {1} [n + 1] = a_ {2} [n] a_ {0} [n + 1] = a_ {1} [n] end {case}}}

куда п это временной индекс и ${ displaystyle +}$ представляет по модулю 2 добавление. Для битовых значений 0 = FALSE или 1 = TRUE это эквивалентно операции XOR.

Поскольку MLS являются периодическими, а регистры сдвига циклически перебирают все возможные двоичные значения (за исключением нулевого вектора), регистры могут быть инициализированы в любое состояние, за исключением нулевого вектора.

Полиномиальная интерпретация

А многочлен над GF (2) может быть связан с регистром сдвига с линейной обратной связью. Он имеет степень длины сдвигового регистра и имеет коэффициенты 0 или 1, соответствующие отводам регистра, которые подают xor ворота. Например, полином, соответствующий рисунку 1, равен Икс⁴ + Икс¹ + 1.

Необходимым и достаточным условием максимальной длины последовательности, сгенерированной LFSR, является то, что соответствующий ей многочлен равен примитивный.^[3]

Выполнение

MLS недорого реализовать в аппаратном или программном обеспечении, а регистры сдвига с обратной связью относительно низкого порядка могут генерировать длинные последовательности; последовательность, сгенерированная с использованием сдвигового регистра длиной 20, равна 2²⁰ - 1 проба (1 048 575 проб).

Свойства последовательностей максимальной длины

MLS обладают следующими свойствами, сформулированными в Соломон Голомб.^[4]

Баланс собственности

Вхождение 0 и 1 в последовательности должно быть примерно одинаковым. Точнее, в последовательности максимальной длины length ${ displaystyle 2 ^ {n} -1}$ Существуют ${ Displaystyle 2 ^ {п-1}}$ те и ${ displaystyle 2 ^ {n-1} -1}$ нули. Количество единиц равно количеству нулей плюс один, поскольку состояние, содержащее только нули, не может возникнуть.

Выполнить свойство

«Выполнение» - это подпоследовательность из последовательных «1» или последовательных «0» в пределах рассматриваемого MLS. Количество прогонов - это количество таких подпоследовательностей.^{[нечеткий]}

Из всех "прогонов" (состоящих из "1" или "0") в последовательности:

Одна половина прогонов имеет длину 1.
Одна четверть пробегов имеет длину 2.
Одна восьмая трасса имеет длину 3.
... так далее. ...

Корреляционное свойство

Циркуляр автокорреляция MLS является Дельта Кронекера функция^[5]^[6] (со смещением постоянного тока и временной задержкой, в зависимости от реализации). По соглашению ± 1, т. Е. Присвоено значение бита 1 ${ displaystyle s = + 1}$ и битовое значение 0 ${ displaystyle s = -1}$ , сопоставление XOR с негативом продукта:

${ Displaystyle R (п) = { гидроразрыва {1} {N}} sum _ {m = 1} ^ {N} s [m] , s ^ {*} [m + n] _ {N} = { begin {case} 1 & { text {if}} n = 0, - { frac {1} {N}} & { text {if}} 0$

куда ${ displaystyle s ^ {*}}$ представляет собой комплексное сопряжение и ${ Displaystyle [м + п] _ {N}}$ представляет круговой сдвиг.

Линейная автокорреляция MLS аппроксимирует дельту Кронекера.

Извлечение импульсных откликов

Если линейный инвариант во времени (LTI) импульсный отклик системы должен быть измерен с помощью MLS, отклик может быть извлечен из измеренного выхода системы. у[п], взяв его круговую взаимную корреляцию с MLS. Это потому, что автокорреляция MLS равно 1 для нулевого запаздывания и почти нулю (−1 /N куда N - длина последовательности) для всех остальных лагов; другими словами, можно сказать, что автокорреляция MLS приближается к единичной импульсной функции по мере увеличения длины MLS.

Если импульсная характеристика системы равна час[п] и MLS s[п], тогда

{ Displaystyle у [п] = (ч * з) [п]. ,}

Взяв взаимную корреляцию относительно s[п] с обеих сторон,

{ displaystyle { phi} _ {sy} = h [n] * { phi} _ {ss} ,}

и полагая φ_SS это импульс (действительно для длинных последовательностей)

{ Displaystyle ч [п] = { phi} _ {sy}. ,}

Для этой цели можно использовать любой сигнал с импульсной автокорреляцией, но сигналы с высокой пик фактор, такие как сам импульс, вызывают импульсные отклики с плохой соотношение сигнал шум. Обычно предполагается, что MLS будет тогда идеальным сигналом, так как он состоит только из полномасштабных значений, а его цифровой пик-фактор является минимальным, 0 дБ.^[7]^[8] Однако после аналоговая реконструкция, резкие скачки в сигнале вызывают сильные межвыборочные пики, ухудшающие пик-фактор на 4-8 дБ или более, увеличиваясь с увеличением длины сигнала, делая его хуже, чем синусоидальная развертка.^[9] Другие сигналы были разработаны с минимальным коэффициентом амплитуды, хотя неизвестно, можно ли его улучшить за пределы 3 дБ.^[10]

Связь с преобразованием Адамара

Кон и Лемпель^[11] показал связь MLS с Преобразование Адамара. Эти отношения позволяют корреляция MLS должен быть вычислен в быстром алгоритме, аналогичном БПФ.

Смотрите также

внешняя ссылка

Бристоу-Джонсон, Роберт. "Небольшое руководство по MLS". - Краткое онлайн-руководство, описывающее, как MLS используется для получения импульсивный ответ из линейная инвариантная во времени система. Также описывает, как нелинейности в системе могут проявляться как ложные выбросы в кажущейся импульсной характеристике.
Хи, Йенс. «Измерение импульсной характеристики с помощью MLS» (PDF). - Документ, описывающий генерацию MLS. Содержит C-код для генерации MLS с использованием до 18-ти ответвлений LFSR и соответствующего преобразования Адамара для извлечения импульсной характеристики.
Керр, Уэсли; Друкер, Дэниел. «Создание М-последовательностей». Лаборатория Джеффри Агирре. Пенсильванский университет.
"Регистры сдвига с линейной обратной связью". Инструменты новой волны. 2005 г. - Свойства последовательностей максимальной длины и подробные таблицы обратной связи для максимальной длины от 7 до 16 777 215 (от 3 до 24 этапов) и частичные таблицы для длин до 4 294 967 295 (от 25 до 32 этапов).
Шефер, Магнус (октябрь 2012 г.). «База данных импульсных характеристик Аахена». Институт систем связи и обработки данных, RWTH Aachen University. V1.4. База данных импульсных характеристик (бинауральных) комнат, созданная с помощью последовательностей максимальной длины]
«Эффективные регистры сдвига, счетчики LFSR и генераторы длинных псевдослучайных последовательностей - устарели» (PDF). Xilinx. Июль 1996 г. XAPP052 v1.1. - Реализация lfsr в ПЛИС включает список ответвлений от 3 до 168 бит

[1] Пудель, Хем Нараян; Робертсон, Уильям М. (2018-10-15). «Многослойный диэлектрический отражатель максимальной длины последовательности». OSA Continuum. 1 (2): 358–372. Дои:10.1364 / OSAC.1.000358. ISSN 2578-7519.

[buracas-2] Buracas GT, Boynton GM (июль 2002 г.). «Эффективный дизайн экспериментов с фМРТ, связанных с событиями, с использованием M-последовательностей». NeuroImage. 16 (3 Pt 1): 801–13. Дои:10.1006 / nimg.2002.1116. PMID 12169264.

[3] «Регистры сдвига с линейной обратной связью - реализация, свойства M-последовательности, таблицы обратной связи»[1], New Wave Instruments (NW), дата обращения 2013.12.03.

[golumb-4] Голомб, Соломон В. (1967). Последовательности регистров сдвига. Холден-Дэй. ISBN 0-89412-048-4.

[5] Якобсен, Финн; Джул, Питер Моллер (04.06.2013). Основы общей линейной акустики. Джон Вили и сыновья. ISBN 978-1118636176. Последовательность максимальной длины - это двоичная последовательность, круговая автокорреляция которой (за исключением небольшой ошибки DC) является дельта-функцией.

[6] Sarwate, D. V .; Пёрсли, М. Б. (1980-05-01). «Кросскорреляционные свойства псевдослучайных и родственных последовательностей». Труды IEEE. 68 (5): 593–619. Дои:10.1109 / PROC.1980.11697. ISSN 0018-9219.

[7] "Небольшое руководство по MLS (последовательность максимальной длины) | dspGuru.com". dspguru.com. Получено 2016-05-19. его среднеквадратичное и пиковое значения равны X, что делает его пик-фактор (пик / среднеквадратичное значение) равным 1, наименьшему из возможных.

[8] «Другие методы электроакустических измерений». www.clear.rice.edu. Получено 2016-05-19. Коэффициент амплитуды для MLS очень близок к 1, поэтому имеет смысл использовать этот тип входного сигнала, когда нам требуется высокое отношение сигнал / шум для наших измерений.

[9] Чан, Ян Х. «Синусоидальное чириканье с разверткой для измерения импульсной характеристики» (PDF). thinksrs.com. Получено 2016-05-19.

[10] Friese, M. (1997-10-01). «Многотональные сигналы с низким коэффициентом амплитуды» (PDF). Транзакции IEEE по коммуникациям. 45 (10): 1338–1344. Дои:10.1109/26.634697. ISSN 0090-6778.

[cohn-11] Cohn, M .; Лемпель, А. (январь 1977 г.). «О быстрых преобразованиях M-последовательностей». IEEE Trans. Инф. Теория. 23 (1): 135–7. Дои:10.1109 / TIT.1977.1055666.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Navigation