WikiDer > Сетевой раздел

А сетевой раздел относится к разложению сети на относительно независимые подсети для их отдельной оптимизации, а также разделения сети из-за выхода из строя сетевых устройств. В обоих случаях ожидается устойчивое к разделению поведение подсетей. Это означает, что даже после того, как сеть разделена на несколько подсистем, она по-прежнему работает правильно.

Например, в сети с несколькими подсетями, где узлы A и B расположены в одной подсети, а узлы C и D - в другой, возникает разделение, если устройство переключения между двумя подсетями выходит из строя. В этом случае узлы A и B больше не могут связываться с узлами C и D, но все узлы A-D работают так же, как и раньше.

Сетевой раздел для оптимизации

Рис. 1. Раздел сети с отбрасыванием наиболее неактуальных взаимодействий между элементами.^[1]

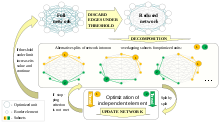
Чтобы разложить NP-жесткий Задача оптимизации сети на подзадачи, сеть может быть разбита на относительно независимые подсети. Чтобы разделить сеть, полезно визуализировать ее как взвешенный полный граф, где каждая вершина соответствует элементу сети, а каждое ребро имеет вес, равный рангу корреляции между каждой парой соответствующих элементов. Затем отбрасываются самые нерелевантные взаимодействия между элементами сети. На основе оставшихся соединений сеть затем делится на относительно независимые подсети.^[1] При этом разные распределения оптимизированных элементов предрасполагают к альтернативным разделениям сети (рис. 1). В случае большой сети оптимизация каждой подсети может выполняться независимо на разных компьютерных кластерах.

Как компромисс CAP

В Теорема CAP основан на трех компромиссах: Последовательность, Доступность, и Допуск разделения. Допуск на разделение в данном контексте означает способность системы обработки данных продолжать обработку данных, даже если сетевой раздел вызывает ошибки связи между подсистемами.^[2]

внешняя ссылка

• Разделение большой сети DOI: 10.13140 / RG.2.2.20183.06565 / 6

Рекомендации