WikiDer > Орбита Марса
Марс имеет орбиту с большой полуосью 1,524 астрономические единицы (228 млн км) и эксцентриситет 0,0934.[1][2] Планета обращается вокруг Солнца за 687 дней[3] и путешествует при этом 9,55 AU,[4] что составляет среднюю орбитальную скорость 24 км / с.
Эксцентриситет больше, чем у любой другой планеты, кроме Меркурия, и это вызывает большую разницу между афелий и перигелий расстояния - 1,6660 и 1,3814 а.е.[5][нужна цитата]
Изменения на орбите
Марс находится в процессе длительного увеличения эксцентриситета.[Почему?] Он достиг минимального значения 0,079 около 19 тысячелетий назад и достигнет максимума около 0,105 примерно через 24 тысячелетия с настоящего момента (а расстояние до перигелия составляет всего 1,3621).астрономические единицы). Орбита иногда близка к круговой: это было 0,002 1,35 миллиона лет назад и будет примерно 0,01 миллиона лет назад.[требуется разъяснение] Максимальный эксцентриситет между этими двумя минимумами составляет 0,12.[6]
Оппозиции
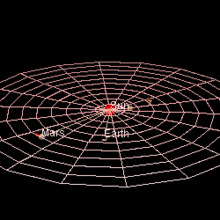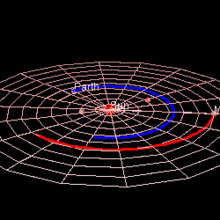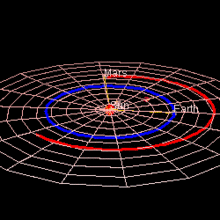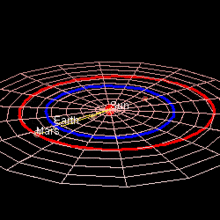
Марс достигает оппозиция когда разница между геоцентрическими долготами Солнца и Солнца составляет 180 °. В момент близкого противостояния (в пределах 8½ дней) расстояние Земля-Марс настолько мало, насколько оно будет достигнуто за эти 780 дней. синодический период.[7] Каждое противодействие имеет какое-то значение, потому что Марс виден с Земли всю ночь, высоко и полностью освещен, но те, которые представляют особый интерес, случаются, когда Марс находится около перигелия, потому что в это время Марс также находится ближе всего к Земле. За одним перигелическим противостоянием следует другое 15 или 17 лет спустя. Фактически, за каждым противодействием следует подобное спустя 7 или 8 синодических периодов, и очень похожее через 37 синодических периодов (79 лет).[8] В так называемом перигелевый оппозиция Марс находится ближе всего к Солнцу и особенно близко к Земле: оппозиция колеблется от примерно 0,68 а.е., когда Марс находится около афелия, до всего около 0,37 а.е., когда Марс находится около перигелия.[9]
Близкие подходы к Земле
Марс подходит к Земле ближе, чем любая другая планета, за исключением ближайшей Венеры - 56 против 40 миллионов км. С годами расстояния уменьшались, и в 2003 году минимальное расстояние составляло 55,76 миллиона км, что ближе, чем любое подобное столкновение за почти 60 000 лет (57617 до н.э.). Этот современный рекорд будет побит в 2287 году, а рекорд до 3000 будет установлен в 2729 году на уровне 55,65. После, в 3818 году, рекорд будет 55,44. Расстояния будут продолжать уменьшаться примерно 24 000 лет.[10]
Историческое значение
До работы Иоганн Кеплер (1571–1630), немецкий астроном, преобладало мнение, что Солнце и планеты вращаются вокруг Земли. Николай Коперник предположил, что все планеты вращаются по кругу вокруг Солнца, но его теория не давала очень удовлетворительных предсказаний и в значительной степени игнорировалась. Когда Кеплер изучал своего босса Тихо БрагеНаблюдая за положением Марса на небе в течение многих ночей, Кеплер понял, что орбита Марса не может быть круговой. После многих лет анализа Кеплер обнаружил, что орбита Марса, вероятно, будет эллипс, с Солнцем в одном из эллипсов точки фокуса. Это, в свою очередь, привело к открытию Кеплера, что все планеты вращаются вокруг Солнца по эллиптическим орбитам, причем Солнце находится в одной из двух фокусных точек. Это стало первым из Три закона движения планет Кеплера.[11][12]
Точность / предсказуемость
С точки зрения всех, кроме самых требовательных, путь Марса прост. Уравнение в Астрономические алгоритмы который предполагает невозмущенную эллиптическую орбиту, предсказывает времена перигелия и афелия с погрешностью «несколько часов».[13] Использование элементов орбиты для вычисления этих расстояний соответствует фактическим средним значениям как минимум с пятью значащими цифрами. Формулы для вычисления положения прямо из элементов орбиты обычно не предоставляют и не требуют поправок на влияние других планет.[14]
Для более высокого уровня точности требуются возмущения планет. Они хорошо известны и считаются достаточно хорошо смоделированными для достижения высокой точности. Это все органы, которые необходимо учитывать даже при решении многих сложных проблем. Когда Альдо Витальяно вычислил дату близкого сближения Марса в далеком прошлом или будущем, он проверил потенциальный эффект, вызванный неопределенностями моделей пояса астероидов, запустив моделирование как с тремя самыми большими астероидами, так и без них, и обнаружил, что эффекты были незначительными.
Наблюдения стали намного лучше, и технологии космической эры заменили старые методы. Э. Майлс Стэндиш писал: «Классические эфемериды прошлых столетий полностью основывались на оптических наблюдениях: почти исключительно, времени прохождения меридионального круга. С появлением планетарного радара, миссий космических кораблей, РСДБ и т. Д. Ситуация для четырех внутренних планеты сильно изменились ». (8.5.1 стр. 10) Для DE405, созданного в 1995 году, оптические наблюдения были прекращены, и, как он писал, «начальные условия для четырех внутренних планет были скорректированы с учетом данных о дальности, в первую очередь…»[15] Известно, что ошибка в DE 405 составляет около 2 км, а теперь составляет менее километра.[16]
Хотя возмущения на Марсе астероидами вызвали проблемы, они также использовались для оценки масс некоторых астероидов.[17] Но улучшение модели пояса астероидов является серьезной проблемой для тех, кто требует или пытается предоставить эфемериды высочайшей точности.[18]
Параметры орбиты
Не более пяти значимые фигуры представлены в следующей таблице Марса. орбитальные элементы. До этого уровня точность, числа очень хорошо совпадают с элементами VSOP87 и вычислениями, производными от них, а также с наилучшим соответствием Стэндиша (JPL) за 250 лет и вычислениями с использованием фактических положений Марса во времени.
| Расстояния и эксцентриситет | (Австралия) | (млн км) |
|---|---|---|
| Большая полуось | 1.5237 | 227.9 |
| Перигелий | 1.3814 | 206.7 |
| Афелий | 1.6660 | 249.2 |
| Средний[19] | 1.5303 | 228.9 |
| Длина окружности | 9.553 | 1429 |
| Ближайший подход к Земле | 0.3727 | 55.76 |
| Наибольшее расстояние от Земли | 2.675 | 400.2 |
| Эксцентриситет | 0.0934 | |
| Углы | (°) | |
| Наклон | 1.850 | |
| Период | (дней) | (годы) |
| Орбитальный | 687.0 | 1.881 |
| Синодический | 779.9 | 2.135 |
| Скорость | (км / с) | |
| Средний | 24.1 | |
| Максимум | 26.5 | |
| Минимум | 22.0 | |
использованная литература
- ^ Simon, J.L .; Bretagnon, P .; Chapront, J .; Chapront-Touzé, M .; Francou, G .; Ласкар, Дж. (Февраль 1994 г.). «Числовые выражения для формул прецессии и средних элементов для Луны и планет». Астрономия и астрофизика. 282 (2): 663–683. Bibcode:1994A & A ... 282..663S.
- ^ Жан Миус, Астрономическая формулаæ для калькуляторов. (Ричмонд, Вирджиния: Willmann-Bell, 1988) 99. Элементы Ф. Э. Росс
- ^ В эфемеридах дней 86 400 секунд. Сидерический и аномальный годы составляют 686.980 дней и 686.996 дней соответственно. (Разница примерно в 20 минут). Сидерический год - это время, необходимое для обращения вокруг Солнца относительно фиксированной системы отсчета. Точнее, сидерический год - это один из способов выразить скорость изменения средней долготы в один момент относительно фиксированного равноденствия. Расчет показывает, сколько времени потребуется, чтобы долгота изменилась на 360 градусов с заданной скоростью. Аномалистический год - это промежуток времени между последовательными прохождениями перигелия или афелия. Он может быть рассчитан так же, как и звездный год, но используется средняя аномалия.
- ^ Жан Миус, Астрономические алгоритмы (Ричмонд, Вирджиния: Willmann-Bell, 1998) 238. Формула Рамануджана достаточно точна.
- ^ Средние значения между 1850 и 2150 годами. Крайние значения в этом диапазоне составляют 1,66635 и 1,38097 австралийских единиц.
- ^ «Архивная копия». Архивировано из оригинал на 2007-09-07. Получено 2007-07-20.CS1 maint: заархивированная копия как заголовок (ссылка на сайт) Расстояние и эксцентриситет Марса с использованием Solex. Создатель Альдо Витальяно
- ^ Синодический период может быть рассчитан как 1 / (1 / p-1 / q), где p и q - меньший и больший звездные периоды.
- ^ Синодический период Марса на 92,9 дня больше, чем его сидерический период в 687,0 дней. Затем он переместился вперед 92,9 / 687,0 умножить на 360, или 48,7 градуса. После семи противостояний он переместился вперед на 341 градус, а после восьми - на 390 градусов; в первом случае его долгота отличается от одного оборота на 19 °, а во втором - на 30 °. Так что тогда ситуации будут аналогичными. Подобные расчеты показывают, что долгота меняется только на 2 ° после 37 противостояний.
- ^ Шихан, Уильям (2 февраля 1997 г.). «Приложение 1: Противостояние Марса, 1901–2035 гг.». Планета Марс: история наблюдений и открытий. Университет Аризоны Press. Архивировано из оригинал 25 июня 2010 г.. Получено 30 января, 2010.
- ^ Миус, Жан (март 2003 г.). "Когда Марс последний раз был так близко?" (PDF). Планетарий: 13.
- ^ Карр, Майкл Х .; Малин, Майкл С.; Белтон, Майкл Дж. (27 июля 2018 г.). "Марс". Британская энциклопедия онлайн. п. 2.
- ^ Уильям Шиэн, Планета Марс: история наблюдений и открытий (Тусон, Аризона: Издательство Аризонского университета, 1996) Глава 1
- ^ Meeus (1998), стр. 269–270
- ^ см., например, Simon et al. (1994) стр. 681
- ^ Стэндиш и Уильямс (2012). «ГЛАВА 8: Орбитальные эфемериды Солнца, Луны и планет» (PDF). Версия 2012 г. Пояснительное приложение
- ^ Как отмечается в Меморандуме JPL 2008 года относительно DE 421, «теперь известно, что ошибка на орбитах Земли и Марса в DE 405 составляет около 2 км, что было хорошей точностью в 1997 году, но намного хуже, чем нынешняя субкилометровая точность».Фолькнер; и другие. (2008). "Планетарные и лунные эфемериды DE421" (PDF). Межведомственный меморандум JPL IOM 343.R-08-003. п. 1
- ^ "астероид". Encyclopdia Britannica. Энциклопедия Britannica Online. Энциклопедия Britannica Inc., 2014. Интернет. 19 августа 2014 г. http://www.britannica.com/EBchecked/topic/39730/asteroid
- ^ "Неопределенность орбиты Марса для годового прогноза составляет около 300 м, как требуется для миссии Марсианской научной лаборатории, но быстро растет в течение времени до и после периода наблюдения космического корабля из-за влияния астероидов с орбитами, близкими к орбитам Марс. Прогнозируемая орбита и неопределенность сильно зависят от используемой модели астероида ».Фолькнер; и другие. (2010). "Неопределенности в планетных эфемеридах JPL" (PDF). Труды Journées. п. 43.
- ^ Среднее расстояние в разы. Постоянный член в VSOP87. Это соответствует среднему значению, взятому из множества коротких равных интервалов времени.