WikiDer > Пинч (физика плазмы)
А ущипнуть сжатие электропроводящего нить к магнитный силы. Дирижер обычно плазма, но также может быть твердым или жидким металл. Щипцы были первым типом устройств, используемых для контролируемого термоядерная реакция.[2]
Это явление также можно назвать Беннетт пинч[3] (после Уиллард Харрисон Беннетт), электромагнитный зажим,[4] магнитный зажим,[5] щепотка эффект[6] или же плазменная щепотка.[7]
Щипки возникают естественным образом при электрических разрядах, таких как молнии,[8] то Аврора,[9] текущие листы,[10] и солнечные вспышки.[11]
Основной механизм
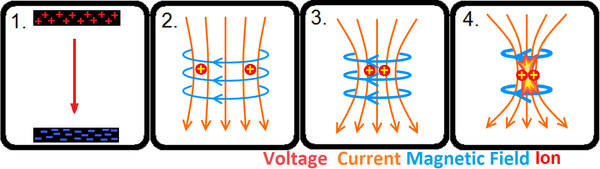
Типы

Щипки существуют в лабораториях и в природе. Штифты отличаются своей геометрией и рабочими силами.[12] К ним относятся:
- Неконтролируемый
- Каждый раз, когда электрический ток движется в больших количествах (например, молния, дуги, искры, разряды), магнитная сила может стягивать плазму. Этого может быть недостаточно для слияния.
- Щипок листа
- Это астрофизический эффект, возникающий из-за огромных слоев заряженных частиц.[13]
- Z-защемление
- Ток течет по оси (или стенкам) цилиндра, пока магнитное поле является азимутальный
- Тета щепотка
- Магнитное поле бежит вниз по оси цилиндра, а электрическое поле находится в азимутальный направление (также называемое тетатроном[14])
- Винт зажим
- Комбинация Z-пинча и тета-пинча [15] (также называемый стабилизированным Z-пинчем или θ-Z пинчем)[16][17]
- Пинч с перевернутым полем
- Это попытка сделать Z-защемление внутри бесконечного цикла. Плазма имеет внутреннее магнитное поле. Когда вы выходите из центра этого кольца, магнитное поле меняет направление. Также называется тороидальным зажимом.
- Обратный зажим
- Это устройство, изначально созданное для термоядерного синтеза, состояло из стержня, окруженного плазмой. Ток прошел через плазму и вернулся по центральному стержню.[18] Эта геометрия немного отличалась от z-пинча тем, что проводник находился в центре, а не по бокам.
- Цилиндрический зажим
- Ортогональный пинч-эффект
- Посуда щепотка
- Щепотка внутри токамаков. Это когда частицы внутри банановой орбиты конденсируются вместе.[19][20]
- MagLIF
- Z-пинч предварительно нагретого, предварительно намагниченного топлива внутри металлической гильзы, который может привести к воспламенению и практической энергии термоядерного синтеза с более мощным импульсным драйвером.[21]
Обычное поведение
Щипки могут стать неустойчивый.[22] Они излучают энергию в виде света через все электромагнитный спектр включая радиоволны, рентгеновские лучи,[23] гамма излучение,[24] синхротронное излучение,[25] и видимый свет. Они также производят нейтроны, как продукт слияния.[26]
Приложения и устройства
Щипки используются для создания Рентгеновские лучи генерируемые интенсивные магнитные поля используются в электромагнитное формование металлов. У них также есть приложения в пучки частиц[27] включая оружие пучка частиц,[28] астрофизические исследования[29] и было предложено использовать их в космических двигателях.[30] Был построен ряд больших щипковых машин для изучения термоядерная энергия; вот несколько:
- MAGPIE Z-щепотка в Имперском колледже. Это пропускает через провод огромное количество тока. В этих условиях проволока становится плазмой и сжимается, образуя плавление.[31]
- Z Pulse Power Facility в Сандийских национальных лабораториях.
- ZETA устройство в Калхэме, Англия
- Симметричный тор Мэдисона в Университете Висконсина, Мэдисон
- Эксперимент с обращенным полем в Италии.
- фокус плотной плазмы в Нью-Джерси
- Университет Невады, Рино (СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ)
- Корнелл Университет (СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ)
- университет Мичигана (СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ)
- Калифорнийский университет в Сан-Диего (СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ)
- Вашингтонский университет (СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ)
- Рурский университет (Германия)
- École Polytechnique (Франция)
- Институт науки Вейцмана (Израиль)
- Universidad Autónoma Metropolitana (Мексика).
Бидоны дробильные с эффектом защемления

Многие энтузиасты высоковольтной электроники создают свои собственные грубые устройства для электромагнитного формования.[32][33][34] Они используют импульсная мощность методы производства тета-щепотки, способной раздавить алюминиевую банку для безалкогольных напитков, с использованием Силы Лоренца создается, когда в емкости индуцируются большие токи сильным магнитным полем первичной катушки.[35][36]
Электромагнитная дробилка для алюминиевых банок состоит из четырех основных компонентов: высокое напряжение ОКРУГ КОЛУМБИЯ источник питания, который обеспечивает источник электроэнергия, большой разряд энергии конденсатор для накопления электроэнергии, выключатель высокого напряжения или разрядники прочная катушка (способная выдерживать высокое магнитное давление), через которую накопленная электрическая энергия может быть быстро разряжена для создания соответственно сильного сжимающего магнитного поля (см. диаграмму ниже).
На практике такое устройство является несколько более сложным, чем предлагает схематическая диаграмма, включая электрические компоненты, которые контролируют ток, чтобы максимизировать результирующий зажим и гарантировать безопасную работу устройства. Подробнее см. Примечания.[37]
История

Первое создание Z-пинча в лаборатории могло произойти в 1790 году в Голландии, когда Мартинус ван Марум создал взрыв, выпустив 100 Лейденские банки в проволоку.[39] Этот феномен не был понят до 1905 года, когда Поллок и Барраклаф[1] исследовали сжатую и деформированную длину медной трубки из молниеотвод после удара молнии. Их анализ показал, что силы, возникающие из-за взаимодействия большого электрического тока с его собственным магнитным полем, могли вызвать сжатие и искажение.[40] Похожий и явно независимый теоретический анализ пинч-эффекта в жидких металлах был опубликован Нортруппом в 1907 году.[41] Следующим важным событием стала публикация в 1934 г. анализа баланса радиального давления в статическом Z-пинче, проведенного авторами. Беннетт[42] (подробности см. в следующем разделе).
После этого экспериментальный и теоретический прогресс в области пинчей был обусловлен термоядерная энергия исследование. В своей статье о Z-пинче с проволочной решеткой: мощный источник рентгеновского излучения для ICF", М. Г. Хейнс и другие., писал в "Ранней истории Z-пинчей".[43]
- В 1946 году Томпсон и Блэкман подали патент на термоядерный реактор на основе тороидального Z-пинча[44] с дополнительным вертикальным магнитным полем. Но в 1954 году Краскал и Шварцшильд[45] опубликовали свою теорию МГД-неустойчивостей в Z-пинче. В 1956 году Курчатов прочитал свою знаменитую лекцию в Харвелле, показав нетепловые нейтроны и наличие м = 0 и м = 1 нестабильности в дейтериевом шнуре.[46] В 1957 году Пис[47] и Брагинский[48][49] независимо предсказал радиационный коллапс в Z-пинче при балансе давления, когда в водороде ток превышает 1,4 МА. (Вязкое, а не резистивное рассеяние магнитной энергии, рассмотренное выше и в[50] однако предотвратит радиационный коллапс).
В 1958 году был проведен первый в мире эксперимент по управляемому термоядерному синтезу с использованием тета-пинч-машины под названием Сцилла I в Лос-Аламосская национальная лаборатория. Цилиндр, наполненный дейтерием, был преобразован в плазму и сжат до 15 миллионов градусов Цельсия под действием тета-пинча.[2] Наконец, в Имперском колледже в 1960 году под руководством Р. Лэтэма Неустойчивость Плато – Рэлея. был показан, и скорость его роста измерена в динамическом Z-пинче.[51]
Анализ равновесия
Одно измерение
В физика плазмы Обычно изучаются три геометрии пинча: θ-пинч, Z-защемление, и винтовой зажим. Они имеют цилиндрическую форму. Цилиндр симметричен в осевом (z) направление и азимутальное (θ) направления. Одномерные пинчи названы по направлению, в котором движется ток.
Θ-пинч
Θ-пинч имеет магнитное поле, направленное в направлении z, и большой диамагнитный ток, направленный в направлении θ. С помощью Закон Ампера (отбрасывая член смещения)
С B это только функция р мы можем упростить это до
Так J указывает в направлении θ.
Таким образом, условие равновесия () для θ-пинча:
θ-пинчи устойчивы к плазменным неустойчивостям; Частично это связано с Теорема Альфвена (также известная как теорема о застывшем потоке).
Z-пинч
Z-пинч имеет магнитное поле в направлении θ и ток J течет в z направление. Опять же, по закону электростатического Ампера
Таким образом, условие равновесия, , для Z-пинча читаем:
Поскольку частицы в плазме в основном движутся по силовым линиям магнитного поля, Z-пинчи ведут их по кругу. Следовательно, они, как правило, обладают отличными удерживающими свойствами.
Винтовой зажим
Винтовой зажим - это попытка объединить аспекты устойчивости θ-пинча и аспекты удержания Z-пинча. Ссылаясь еще раз на закон Ампера,
Но на этот раз B поле имеет θ-компоненту и а z компонент
Так что на этот раз J имеет компонент в z направление и компонент в направлении θ.
Наконец, условие равновесия () для зажима винта:
Винтовой зажим через сталкивающиеся оптические вихри
В винтовой зажим могут образовываться в лазерной плазме при столкновении оптических вихрей ультракороткой длительности.[52] Для этого оптические вихри должны быть сопряжены по фазе.[53]Распределение магнитного поля здесь снова дается законом Ампера:
Два измерения
Распространенная проблема с одномерными шнурами - это торцевые потери. Большая часть движения частиц происходит вдоль магнитного поля. С θ-зажимом и зажимом для винта это очень быстро выводит частицы из конца машины, что приводит к потере массы и энергии. Помимо этой проблемы, Z-пинч имеет серьезные проблемы со стабильностью. Хотя частицы могут в некоторой степени отражаться магнитные зеркала, даже они позволяют проходить большому количеству частиц. Распространенный метод борьбы с этими концевыми потерями - изогнуть цилиндр в тор. К сожалению, это нарушает θ-симметрию, поскольку пути на внутренней части (внутренней стороне) тора короче, чем аналогичные пути на внешней части (внешней стороне). Таким образом, нужна новая теория. Это дает начало знаменитому Уравнение Грэда – Шафранова.. Численные решения уравнения Грэда – Шафранова также привели к некоторым состояниям равновесия, в первую очередь к равновесию пинч с перевернутым полем.
Три измерения
По состоянию на 2015 год не существует последовательной аналитической теории для трехмерных равновесий. Общий подход к поиску трехмерных равновесий состоит в решении вакуумных идеальных МГД-уравнений. Численные решения дали планы для стеллараторы. Некоторые машины используют преимущества методов упрощения, таких как спиральная симметрия (например, эксперимент по спиральной симметрии Университета Висконсина). Однако для произвольной трехмерной конфигурации существует соотношение равновесия, подобное соотношению 1-D конфигураций:[54]
Где κ - вектор кривизны, определяемый как:
с б единичный вектор, касательный к B.
Формальное лечение

Отношение Беннета
Рассмотрим цилиндрический столб полностью ионизированной квазинейтральной плазмы с осевым электрическим полем, создающим осевую плотность тока, j, и связанное с ним азимутальное магнитное поле, B. Поскольку ток течет через собственное магнитное поле, создается пинч с направленной внутрь радиальной плотностью силы j x B. В устойчивом состоянии с уравновешиванием сил:
где ∇п - градиент магнитного давления, а пе и пя - электронное и ионное давление соответственно. Затем используя Уравнение Максвелла и закон идеального газа , получаем:
- (соотношение Беннета)
куда N - количество электронов на единицу длины вдоль оси, Те и Тя - температуры электронов и ионов, я - полный ток пучка, а k это Постоянная Больцмана.
Обобщенное соотношение Беннета
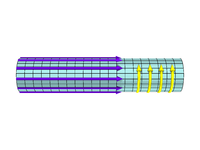
В обобщенное соотношение Беннета Рассматривается цилиндрический плазменный пинч с токопроводящим магнитным полем, вращающийся с угловой частотой ω. Вдоль оси плазменного цилиндра течет плотность тока jz, в результате чего возникает азимутальное магнитное поле cφ. Первоначально получено Witalis,[57] обобщенное соотношение Беннета приводит к:[58]
- где токопроводящая цилиндрическая плазма с направленным магнитным полем имеет радиус а,
- J0 - полный момент инерции относительно оси z,
- WKin это кинетическая энергия на единицу длины за счет движения балки поперек оси балки
- WBz является самосогласованным Bz энергия на единицу длины
- WEz является самосогласованным Ez энергия на единицу длины
- Wk термокинетическая энергия на единицу длины
- я(а) - аксиальный ток внутри радиуса а (р на схеме)
- N(а) - общее количество частиц на единицу длины
- Eр радиальное электрическое поле
- Eφ вращательное электрическое поле
Положительные члены в уравнении - это силы расширения, а отрицательные - силы сжатия балки.
Отношение Карлквиста
Соотношение Карлквиста, опубликованное Пер Карлквист в 1988 г.[12] представляет собой специализацию обобщенного соотношения Беннета (см. выше) для случая, когда кинетическое давление на границе пинча намного меньше, чем во внутренних частях. Это принимает форму
и применимо для многих космических плазм.

Отношение Карлквиста можно проиллюстрировать (см. Справа), указав полный ток (я) от количества частиц на единицу длины (N) в крайнем случае Беннета. На диаграмме показаны четыре физически различных региона. Температура плазмы довольно низкая (Тя = Те = Тп = 20 K), содержащий в основном водород со средней массой 3 × 10−27 кг. Термокинетическая энергия Wk >> πa2 пk(а). Кривые ΔWBz показывают различное количество избыточной магнитной энергии на единицу длины из-за осевого магнитного поля Bz. Плазма считается невращающейся, а кинетическое давление на краях намного меньше, чем внутри.
Регионы диаграммы: (а) В верхнем левом углу преобладает сила сжатия. (b) По направлению ко дну кинетическое давление, направленное наружу, уравновешивает магнитное давление внутрь, и общее давление остается постоянным. (c) Справа от вертикальной прямой ΔWBz = 0, магнитное давление уравновешивает гравитационное давление, и сила сжатия пренебрежимо мала. (г) Слева от наклонной кривой ΔWBz = 0, гравитационная сила ничтожна. Обратите внимание, что диаграмма показывает частный случай отношения Карлквиста, и если его заменить более общим отношением Беннета, то обозначенные области диаграммы недействительны.
Карлквист далее отмечает, что, используя приведенные выше отношения и производную, можно описать пинч Беннета, Критерий джинсов (для гравитационной неустойчивости[59] в одном и двух измерениях), бессиловые магнитные поля, гравитационно-сбалансированные магнитные давления и непрерывные переходы между этими состояниями.
Ссылки в культуре
Беллетризованный пинч-генерирующее устройство использовался в одиннадцать друзей Оушена, где он использовался для отключения электросети Лас-Вегаса на время, достаточное для того, чтобы персонажи начали свое ограбление.[60]
Смотрите также
- Сила термоядерного синтеза
- Симметричный тор Мэдисона (щепотка перевернутого поля)
- Генератор сжатия потока с взрывной накачкой
- Магнеформинг
- Список статей по плазме (физике)
Рекомендации
- ^ а б Поллок Дж. А. и Барраклаф С. (1905) Proc. R. Soc. Новый Южный Уэльс 39 131
- ^ а б Филлипс, Джеймс. «Магнитный синтез». Los Alamos Science Winter 1983: 64-67. Интернет. 4 апреля 2013 г.
- ^ См., Например, Buneman, O., "Беннет Пинч" (1961) Физика плазмы, Отредактированный Джеймсом Э. Драммондом. LOC 60-12766. Publ. McGraw-Hill, Inc., Нью-Йорк, 1961, стр.202.
- ^ Ли, S (1983). «Энергетический баланс и радиус электромагнитно защемленных плазменных столбов». Физика плазмы. 25 (5): 571–576. Bibcode:1983ПлФ ... 25..571л. Дои:10.1088/0032-1028/25/5/009.
- ^ Шмидт, Гельмут (1966). «Формирование магнитного пинча в InSb и возможность инверсии населенности в пинче». Физический обзор. 149 (2): 564–573. Bibcode:1966ПхРв..149..564С. Дои:10.1103 / Physrev.149.564.
- ^ Северный, А. Б. (1959). «О появлении космических лучей в пинч-эффекте в солнечных вспышках». Советская астрономия. 3: 887. Bibcode:1959Сва ..... 3..887С.
- ^ Зуева, Н. М .; Соловьев, Л. С .; Морозов, А. И. (1976). «Нелинейная неустойчивость плазменных шнуров». Журнал экспериментальной и теоретической физики Letters. 23: 256. Bibcode:1976JETPL..23..256Z.
- ^ Rai, J .; Сингх, А. К .; Саха, С. К. (1973). «Магнитное поле в обратном канале молнии». Индийский журнал радио и космической физики. 2: 240–242. Bibcode:1973IJRSP ... 2..240R.
- ^ Гальперин Ю. Я.; Зеленый, Л. М .; Кузнецова, М. М. (1986). «Сжатие продольных токов как возможный механизм образования лучевых форм сияний». Космические исследования. 24: 865–874. Bibcode:1986КосИс..24..865Г.
- ^ Сыроватский С.И. (1981). «Пинч-листы и пересоединение в астрофизике». Ежегодный обзор астрономии и астрофизики. 19: 163–229. Bibcode:1981ARA & A..19..163S. Дои:10.1146 / annurev.aa.19.090181.001115.
- ^ Айрапетян, В. С .; Вихрев, В. В .; Иванов, В. В .; Розанова, Г. А. (1990). «Пинчевый механизм энерговыделения звездных вспышек». Астрофизика. 32 (3): 230–235. Bibcode:1990Ап ..... 32..230А. Дои:10.1007 / bf01005504. S2CID 120883355.
- ^ а б Карлквист, Пер (1988) "Космические электрические токи и обобщенное соотношение Беннета" Астрофизика и космическая наука т. 144, нет. 1-2, май 1988 г., стр. 73-84
- ^ Бискамп, Дитер (1997) Нелинейная магнитогидродинамика Cambridge University Press, Кембридж, Англия, стр. 130, ISBN 0-521-59918-0
- ^ Видеть Словарь по материаловедению и физике высоких энергий стр.315 ISBN 0-8493-2889-6
- ^ Шривастава, К. М .; Вяс, Д. Н. (1982) "Нелинейный анализ устойчивости винтового зажима" Астрофизика и космическая наука, т. 86, нет. 1, август 1982 г., стр. 71-89
- ^ Видеть "МГД-равновесия »в книге« Введение в физику плазмы »И. Х. Хатчинсона (2001)
- ^ Шривастава, К. М .; Валбрук Ф. (1976). «Об устойчивости винтового зажима в модели CGL». Журнал физики плазмы. 16 (3): 261. Bibcode:1976JPlPh..16..261S. Дои:10.1017 / s0022377800020201.CS1 maint: использует параметр авторов (связь)
- ^ «Обратный пинч-эффект» Андерсон и др. Физика жидкостей, Том 1, Выпуск 6, с.489-494
- ^ Helander, P .; и другие. (2005). «Влияние безиндуктивного токового привода на транспорт токамаков». Физика плазмы и управляемый синтез. 47 (12B): B151 – B163. Bibcode:2005PPCF ... 47B.151H. Дои:10.1088 / 0741-3335 / 47 / 12b / s12.
- ^ «Физика плазмы: третье издание», стр. 266 https://books.google.co.uk/books?id=4cHkd77TSHcC&pg=PA266&dq=Ware+pinch&hl=en&sa=X&ei=aZsVVdvZF5L8gwSO_oDoDw&ved=0CCYQ6AEwAQ#V&fare=onepage&pin
- ^ Слуц, Стивен; Веси, Роджер А. (2012). "Намагниченный инерционный синтез с высоким коэффициентом усиления". Письма с физическими проверками. 108 (2): 025003. Bibcode:2012PhRvL.108b5003S. Дои:10.1103 / PhysRevLett.108.025003. PMID 22324693.
- ^ Харди, П. Э. (1982). «Винтовая и пинчинговая неустойчивость сверхзвуковых расширяющихся струй во внегалактических радиоисточниках». Астрофизический журнал. 257: 509–526. Bibcode:1982ApJ ... 257..509H. Дои:10.1086/160008.
- ^ Pereira, N.R .; и другие. (1988). «[Рентгеновские лучи от Z-пинчей на генераторах релятивистских электронных пучков]». Журнал прикладной физики. 64 (3): R1 – R27. Bibcode:1988ЯП .... 64 .... 1П. Дои:10.1063/1.341808.
- ^ Ву, Мэй; Чен, Ли; Ли, Ти-Пей (2005). «Поляризация в гамма-всплесках, вызванных щипковым разрядом». Китайский журнал астрономии и астрофизики. 5 (1): 57–64. arXiv:астро-ph / 0501334. Bibcode:2005ЧЯА ... 5 ... 57Вт. Дои:10.1088/1009-9271/5/1/007. S2CID 121943.
- ^ Ператт, А.Л. "Синхротронное излучение пучков защемленных частиц", (1998) Физика плазмы: VII Lawpp 97: Материалы латиноамериканского семинара 1997 года по физике плазмы, под редакцией Пабло Мартина, Хулио Пуэрта, Пабло Мартмна, со ссылкой на Мейерович, Б. Э."Электромагнитный коллапс. Проблемы устойчивости, выброса излучения и эволюции плотного пинча" (1984) Отчеты по физике, Том 104, Выпуск 5, стр. 259-346.
- ^ Андерсон, Оскар А .; и другие. (1958). «Производство нейтронов в линейных пинчах дейтерия». Физический обзор. 110 (6): 1375–1387. Bibcode:1958ПхРв..110.1375А. Дои:10.1103 / Physrev.110.1375.
- ^ Рютов Д.Д .; Derzon, M. S .; Мацен, М. К (2000). «Физика быстрых Z-пинчей». Обзоры современной физики. 72 (1): 167–223. Bibcode:2000РвМП ... 72..167Р. Дои:10.1103 / revmodphys.72.167.
- ^ Андре Гспонер "Физика распространения высокоинтенсивных пучков частиц высоких энергий в плазме открытого и космического пространства" (2004) https://arxiv.org/abs/physics/0409157
- ^ Ператт, Энтони Л. "Роль пучков частиц и электрических токов в плазменной Вселенной" (1988) Лазерные лучи и пучки частиц (ISSN 0263-0346), т. 6, август 1988 г., стр. 471-491.
- ^ "Разработка технологии импульсного плазменного двигателя Z-Pinch" Заключительный отчет Отдел перспективных концепций (ED04) Центр космических полетов им. Маршалла 8 октября 2010 г., Тара Полсгроув, и др.
- ^ http://dorland.pp.ph.ic.ac.uk/magpie/?page_id=239 В архиве 2014-11-05 в Wayback Machine "Wire Arrays Z-Pinch" дата обращения: 27.03.2015.
- ^ ЛаПуант, Роберт. «Высоковольтные приборы и эксперименты». Получено 21 февраля, 2013.
- ^ Тристан. "Электромагнитная консервная дробилка". Получено 21 февраля, 2013.
- ^ Боррос, Сэм. "Твердотельная консервная дробилка". Получено 21 февраля, 2013.
- ^ «МагнитоПулС». интернет сайт. МАГНИТ-ФИЗИК Dr. Steingroever GmbH. 2002. Архивировано с оригинал на 2003-05-22. Получено 21 февраля, 2013.
- ^ «Промышленное применение технологии электромагнитных импульсов» (PDF). белая бумага. PSTproducts GmbH. Июнь 2009 г. Архивировано с оригинал (PDF) 15 июля 2011 г.. Получено 21 февраля, 2013.
- ^ Примеры электромагнитных дробилок можно найти на сайте (а) Боба ЛаПойнта на Высоковольтные устройства и эксперименты (б) Тристрана Электромагнитная дробилка для банок (включая схему) (c) Сэм Боррос Твердотельная консервная дробилка
- ^ См. Также Центр истории IEEE "Эволюция логотипа IEEE"Март 1963 года; см. Также комментарии в"Лаборатория астрофизики"
- ^ ван Марум М 1790 Proc. 4-й Int. Конф. на плотных Z-защелках (Ванкувер 1997) (Am. Inst. Phys. Woodbury, Нью-Йорк, 1997) Фронтиспис и стр. Ii
- ^ Р. С. Пиз, "Электромагнитный зажим: от Поллок к Совместный европейский тор", "Лекция в память о Поллоке за 1984 год, прочитанная в Сиднейском университете 28 ноября 1984 года " В архиве 2006-05-29 в Wayback Machine
- ^ Нортрап, Эдвин Ф. (1907). «Некоторые недавно наблюдаемые проявления сил внутри электрического проводника». Физический обзор. Серия I. Американское физическое общество (APS). 24 (6): 474–497. Bibcode:1907ФРви..24..474Н. Дои:10.1103 / Physrevseriesi.24.474. ISSN 1536-6065.
- ^ Беннетт, Уиллард H (1934). «Магнитно-самофокусирующиеся потоки». Phys. Rev. 45 (12): 890–897. Bibcode:1934ПхРв ... 45..890Б. Дои:10.1103 / Physrev.45.890.
- ^ Haines, MG; Сэнфорд, Т. В. Л; Смирнов, В П (2005). «Проволочный Z-пинч: мощный источник рентгеновского излучения для ICF». Plasma Phys. Контроль. Слияние. 47 (12B): B1 – B11. Bibcode:2005PPCF ... 47B ... 1H. Дои:10.1088 / 0741-3335 / 47 / 12b / s01.
- ^ Томпсон, Г. П.; Блэкман; Хейнс, М. Г. (1996). «Историческая перспектива: пятьдесят лет исследований управляемого термоядерного синтеза». Plasma Phys. Контроль. Слияние. 38 (5): 643–656. Bibcode:1996PPCF ... 38..643H. Дои:10.1088/0741-3335/38/5/001.
- ^ Крускал, М Д; Шварцшильд (1954). «Некоторые нестабильности полностью ионизированной плазмы». Proc. R. Soc. Лондон. А. 223 (1154): 348–360. Bibcode:1954RSPSA.223..348K. Дои:10.1098 / rspa.1954.0120. S2CID 121125652.
- ^ Курчатов И В (1957) J. Nucl. Энергия 4 193
- ^ Пиз Р. С. (1957). «Равновесные характеристики защемленного газового разряда, охлаждаемого тормозным излучением». Proc. Phys. Soc. Лондон. 70 (1): 11–23. Bibcode:1957ПСБ ... 70 ... 11П. Дои:10.1088/0370-1301/70/1/304.
- ^ Брагинский С И 1957 Ж. Эксп. Теор. Физ 33 645
- ^ Брагинский С И 1958 Сов. Физика — ЖЭТФ. 6 494
- ^ Haines M G и другие. 2005 Phys. Rev. Lett.. Отправлено; см. также EPS Conf. по физике плазмы 2004 (Лондон, Великобритания), статья 73.
- ^ Curzon, F L; и другие. (1960). «Эксперименты по скорости роста поверхностных неустойчивостей в линейном защемленном разряде». Proc. R. Soc. Лондон. А. 257 (1290): 386–401. Bibcode:1960RSPSA.257..386C. Дои:10.1098 / rspa.1960.0158. S2CID 96283997.
- ^ А.Ю. Окулов. "Лазерный сингулярный тета-пинч", Письма в Phys.Lett.A, v.374, 4523-4527, (2010)
- ^ Оптическое ОВФ и электромагнитные импульсы
- ^ Идеальная магнитогидродинамика: современные перспективы в энергетике. Джеффри П. Фрейдберг. Массачусетский Институт Технологий. Кембридж, Массачусетс. Plenum Press - Нью-Йорк и Лондон - 1987 г. (стр. 86 и 95)
- ^ Трубников, Борис А (1992). «Новая гипотеза генерации космических лучей в плазменных шнурах». IEEE Transactions по науке о плазме. 20 (6): 898–904. Bibcode:1992ITPS ... 20..898T. Дои:10.1109/27.199547.
- ^ «Конфигурация ПЛАЗМАК и шаровая молния» (PDF В архиве 2006-07-15 на Wayback Machine) представлены на Международном симпозиуме по шаровой молнии; Июль 1988 г.
- ^ Виталис, Э.А. "Плазмофизические аспекты пучков заряженных частиц" (1981) Physical Review A - Общая физика, 3-я серия, т. 24 ноября 1981 г., стр. 2758–2764
- ^ Энтони Л. Ператт, "Физика плазменной Вселенной", 1992 г., Springer-Verlag, ISBN 0-387-97575-6
- ^ Джинс, Дж. Х. (1902). «Устойчивость сферической туманности». Фил. Пер. R. Soc. Лондон. А. 199 (312–320): 1–53. Bibcode:1902RSPTA.199 .... 1J. Дои:10.1098 / рста.1902.0012.
- ^ "Мошенничество с физикой" одиннадцати друзей Оушена'". Американское физическое общество. Март 2002 г.
внешняя ссылка
- Примеры электромагнитно сморщенных монет и раздавленных банок.
- Теория электромагнитной усадки монет
- Известная история «усадки квартала»
- Может раздавить информацию, в том числе с помощью электромагнетизма.
- Проект MAGPIE в Имперском колледже Лондона используется для изучения имплозий Z-пинча проволочной решетки.






















![{egin {выровнено} {frac {1} {4}} {frac {partial ^ {2} J_ {0}} {partial t ^ {2}}} = {} & W_ {perp {ext {kin}}} + Дельта W_ {E_ {z}} + Дельта W_ {B_ {z}} + Дельта W_ {k} - {frac {mu _ {0}} {8pi}} I ^ {2} (a) [8pt] & {} - {frac {1} {2}} G {overline {m}} ^ {2} N ^ {2} (a) + {frac {1} {2}} pi a ^ {2} epsilon _ { 0} влево (E_ {r} ^ {2} (a) -E_ {phi} ^ {2} (a) ight) end {align}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71e972f92a0d232a7244df3fa2ed04d57711196f)
