WikiDer > Числовой диапазон продуктов - Википедия

Учитывая Гильбертово пространство с тензорное произведение структура числовой диапазон продукта определяется как числовой диапазон относительно подмножества векторов-продуктов. В некоторых ситуациях, особенно в контексте квантовая механика числовой диапазон продукта известен как местный числовой диапазон

Вступление

Позволять ${ displaystyle X}$ быть оператором, действующим на ${ displaystyle N}$-мерное гильбертово пространство ${ displaystyle { mathcal {H}} _ {N}}$. Позволять ${ Displaystyle mathrm { Lambda} (X)}$ обозначить его числовой диапазон, т.е. набор всех ${ displaystyle lambda}$ такое, что существует нормализованное состояние ${ displaystyle {| psi rangle} in { mathcal {H}} _ {N}}$, ${ displaystyle || psi || = 1}$, что удовлетворяет ${ Displaystyle { langle psi |} X {| psi rangle} = lambda}$.

Аналогичное понятие можно определить для операторов, действующих в составном гильбертовом пространстве со структурой тензорного произведения. Рассмотрим сначала двудольное гильбертово пространство, ${ displaystyle { mathcal {H}} _ {N} = { mathcal {H}} _ {K} otimes { mathcal {H}} _ {M},}$ составного измерения ${ displaystyle N = KM}$.

Позволять ${ displaystyle X}$ - оператор, действующий в составном гильбертовом пространстве. Мы определяем числовой диапазон продукта ${ Displaystyle mathrm { Lambda} ^ {! otimes} ! left (X right)}$ из ${ displaystyle X}$, относительно структуры тензорного произведения ${ displaystyle { mathcal {H}} _ {N}}$, так как ${ Displaystyle mathrm { Lambda} ^ {! otimes} ! left (X right) = left {{ langle psi _ {A} otimes psi _ {B} |} X {| psi _ {A} otimes psi _ {B} rangle}: {| psi _ {A} rangle} in { mathcal {H}} _ {K}, {| psi _ {B} rangle} in { mathcal {H}} _ {M} right },}$ куда ${ displaystyle {| psi _ {A} rangle} in { mathcal {H}} _ {K}}$ и ${ displaystyle {| psi _ {B} rangle} in { mathcal {H}} _ {M}}$ нормализованы.

Числовой радиус продукта

Позволять ${ displaystyle { mathcal {H}} _ {N} = { mathcal {H}} _ {K} otimes { mathcal {H}} _ {M}}$ - тензорное произведение гильбертова пространства. Мы определяем числовой радиус продукта ${ displaystyle r ^ { otimes} (X)}$ из ${ displaystyle X}$, относительно этой тензорной структуры произведения, как ${ displaystyle r ^ { otimes} (X) = max {| z |: z in mathrm { Lambda} ^ {! otimes} ! left (X right) }.}$

Обозначение

Понятие числового диапазона данного оператора, также называемого «полем значений», широко изучалось в течение последних нескольких десятилетий, и его полезность в квантовой теории была подчеркнута. Известно несколько обобщений числового диапазона. В частности, Маркус ввел понятие разложимого числового диапазона ’’ ’, свойства которого представляют значительный интерес.

Числовой диапазон произведения можно рассматривать как частный случай разложимого числового диапазона, определенного для операторов, действующих в гильбертовом пространстве тензорного произведения. Это понятие также можно рассматривать как числовой диапазон относительный в соответствующую подгруппу ${ Displaystyle U (K) раз U (M)}$ полной унитарной группы ${ displaystyle U (км)}$.

Характеристики числового ряда продуктов

Этот раздел пуст. Вы можете помочь добавляя к этому. (Апрель 2012 г.)

Общий случай

Нетрудно установить основные свойства числового диапазона произведения, которые не зависят от разбиения гильбертова пространства и от структуры оператора. Мы перечисляем их ниже, оставляя некоторые простые вещи без доказательств.

Основные свойства

Топологические факты о числовом диапазоне произведений для операторов общего вида.

1. Числовой диапазон продуктов образует связный набор в комплексной плоскости. Это верно, потому что числовой диапазон продуктов представляет собой непрерывное изображение связанного набора.
2. Числовой диапазон продукта является субаддитивным. Для всех ${ displaystyle A, B in mathbb {M} _ {n}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left (A + B right) subset mathrm { Lambda} ^ {! otimes} ! left (A right ) + mathrm { Lambda} ^ {! otimes} ! left (B right).}$
3. Для всех ${ displaystyle A in mathbb {M} _ {n}}$ и ${ Displaystyle альфа в mathbb {C}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({A + alpha mathbf {I}} right) = mathrm { Lambda} ^ {! otimes} ! left (A right) + alpha.}$
4. Для всех ${ displaystyle A in mathbb {M} _ {n}}$ и ${ Displaystyle альфа в mathbb {C}}$ ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({ alpha A} right) = alpha mathrm { Lambda} ^ {! otimes} ! left ( {A} right).}$
5. Для всех ${ displaystyle A in mathbb {M} _ {m times n}}$ ${ Displaystyle mathrm { Lambda} ^ {! otimes} ! left ({(U otimes V) A (U otimes V) ^ { dagger}} right) = mathrm { Lambda } ^ {! otimes} ! left ({A} right),}$ для унитарного ${ Displaystyle U in mathbb {M} _ {m}}$ и ${ displaystyle V in mathbb {M} _ {n}}$.
6. Позволять ${ displaystyle A in mathbb {M} _ {m}}$ и ${ displaystyle B in mathbb {M} _ {n}}$

• Если один из них нормальный, то числовой диапазон их тензорного произведения совпадает с выпуклой оболочкой числового диапазона произведения, ${ displaystyle mathrm { Lambda} (A otimes B) = mathrm {Co} ( mathrm { Lambda} ^ {! otimes} ! left ({A otimes B} right)) .}$
• Если ${ displaystyle e ^ {я theta} A}$ положительно полуопределен для некоторых ${ displaystyle theta in [0,2 pi)}$, тогда ${ displaystyle mathrm { Lambda} (A otimes B) = mathrm { Lambda} ^ {! otimes} ! left ({A otimes B} right).}$
• Позволять ${ displaystyle H (A) = { frac {1} {2}} (A + A ^ { dagger})}$ и ${ Displaystyle S (A) = { гидроразрыва {1} {2}} (A-A ^ { dagger})}$.

1. Для всех ${ displaystyle A in mathbb {M} _ {n}}$, у нас есть ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({H (A)} right) = mathrm {Re} mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$ и ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({S (A)} right) = i , mathrm {Im} mathrm { Lambda} ^ {! otimes} ! left ({A} right).}$

Выпуклость

Числовой диапазон продукта не обязательно должен быть выпуклым. Рассмотрим следующий простой пример. Позволять

${ displaystyle A = left ({ begin {array} {cc} 1 & 0 0 & 0 end {array}} right) otimes left ({ begin {array} {cc} 1 & 0 0 & 0 end {array}} right) + i left ({ begin {array} {cc} 0 & 0 0 & 1 end {array}} right) otimes left ({ begin {array} {cc} 0 & 0 0 & 1 end {array}} right).}$

Матрица ${ displaystyle A}$ определенная выше матрица с собственными значениями ${ displaystyle 0,1, i}$. Легко заметить, что ${ displaystyle 1 in mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$ и ${ displaystyle i in mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$, но ${ displaystyle (1 + я) / 2 not in mathrm { Lambda} ^ {! otimes} ! left ({A} right)}$. Фактически, прямым вычислением мы имеем ${ displaystyle mathrm { Lambda} ^ {! otimes} ! left ({A} right) = left {x + yi: 0 leq x, 0 leq y, { sqrt { x}} + { sqrt {y}} leq 1 right }.}$

Числовой диапазон продуктов матрицы ${ displaystyle A}$ представлен ниже.

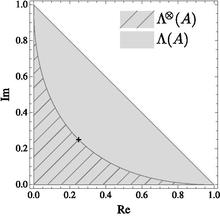
Сравнение числового диапазона (серый треугольник) и числового диапазона произведения (штриховой набор) для матрицы A.

Числовой диапазон продукта образует непустое множество для общего оператора. В частности, он содержит барицентр спектра.

Барицентр

Числовой диапазон продукта ${ displaystyle A in mathbb {M} _ {K times M}}$ включает барицентр спектра, ${ displaystyle { frac {1} {KM}} ; { mathrm {tr}} A in mathrm { Lambda} ^ {! otimes} ! left ({A} right ).}$

Числовой радиус продукта - это векторная норма матриц, но не матричная норма. Числовой радиус произведения инвариантен относительно локальных унитаров, имеющих тензорную структуру произведения.

Рекомендации

• З. Пухала, П. Гаврон, Я.А. Мищак, Ł. Сковронек, М.-. Цой, К. yczkowski, "Числовой диапазон продукта в пространстве с тензорной структурой произведения", Linear Algebra Appl., 434 (2011) 327-342. Дои:10.1016 / j.laa.2010.08.026 arXiv:1008.3482.
• П. Гаврон, З. Пухала, Я. А. Мищак, Ł. Skowronek, K. yczkowski, "Ограниченный числовой диапазон: универсальный инструмент в теории квантовой информации", J. Math. Phys. 51, 102204 (2010). Дои:10.1063/1.3496901 arXiv:0905.3646.