WikiDer > Теорема о проекции среза
В математика, то теорема о проекции, центральная теорема среза или же Теорема Фурье-среза в двух измерениях заявляет, что результаты следующих двух вычислений равны:
- Возьмем двумерную функцию ж(р), проект (например, используя Преобразование радона) на (одномерную) прямую и преобразование Фурье этой проекции.
- Возьмите ту же функцию, но сначала выполните двумерное преобразование Фурье, а затем ломтик это через его начало, которое параллельно линии проекции.
В терминах оператора, если
- F1 и F2 - упомянутые выше 1- и 2-мерные операторы преобразования Фурье,
- п1 - это оператор проекции (который проецирует двумерную функцию на одномерную линию),
- S1 является оператором среза (который извлекает одномерный центральный срез из функции),
тогда
Эту идею можно распространить на более высокие измерения.
Эта теорема используется, например, при анализе медицинскихCT сканирование, где «проекция» - это рентгеновское изображение внутреннего органа. Видно, что преобразования Фурье этих изображений представляют собой срезы через преобразование Фурье трехмерной плотности внутреннего органа, и эти срезы могут быть интерполированы для построения полного преобразования Фурье этой плотности. Затем обратное преобразование Фурье используется для восстановления трехмерной плотности объекта. Этот метод был впервые получен Рональд Н. Брейсвелл в 1956 г. по проблеме радиоастрономии.[1]
Теорема о проекционном срезе в N размеры
В N размеры, теорема о проекции заявляет, чтопреобразование Фурье из проекция из N-мерная функцияж(р) на м-размерный линейное подмногообразиеравно м-размерный ломтик из N-мерное преобразование Фурье этой функции, состоящей из м-мерное линейное подмногообразие через начало координат в пространстве Фурье, параллельное проекционному подмногообразию. В терминах оператора:
Обобщенная теорема Фурье-среза
Помимо обобщения N размерности, теорема о проекции-срезе может быть дополнительно обобщена с произвольной заменой базиса.[2] Для удобства обозначений мы считаем изменение базиса в виде B, N-к-N обратимая матрица, работающая на N-мерные векторы-столбцы. Тогда Обобщенная теорема Фурье-среза можно сформулировать как
Доказательство в двух измерениях
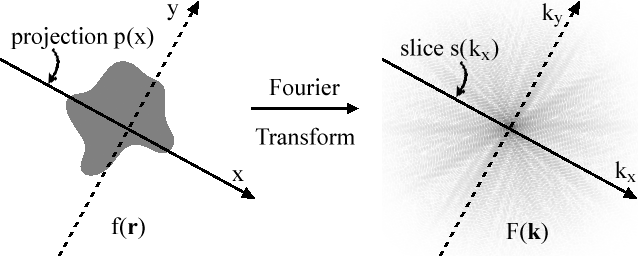
Теорема о проекции-срезе легко доказывается для случая двух измерений. Без ограничения общности мы можем принять за линию проекции прямую проекции. Икс-axis. Нет никакой потери общности, потому что, если мы используем смещенную и повернутую линию, закон все еще применяется. Использование сдвинутой линии (по оси y) дает такую же проекцию и, следовательно, те же результаты одномерного преобразования Фурье. Повернутая функция - это пара Фурье повернутого преобразования Фурье, для которой теорема снова верна.
Если ж(Икс, у) - двумерная функция, то проекция ж(Икс, у) на Икс ось п(Икс) куда
Преобразование Фурье является
Затем ломтик
что является просто преобразованием Фурье п(Икс). Доказательство для более высоких размерностей легко обобщается из приведенного выше примера.
Цикл FHA
Если двумерная функция ж(р) симметрично по кругу, его можно представить в виде ж(р), куда р = |р|, В этом случае проекция на любую линию проекции будет Преобразование Абеля из ж(р). Двумерный преобразование Фурьеиз ж(р) будет циркулярно-симметричной функцией, заданной нулевым порядком Преобразование Ганкеля из ж(р), который, следовательно, также будет представлять любой срез источника. Теорема проекции-среза затем утверждает, что преобразование Фурье проекции равно срезу или
куда А1 представляет собой оператор преобразования Абеля, проецирующий двумерную симметричную по кругу функцию на одномерную линию, F1 представляет собой одномерный оператор преобразования Фурье, а ЧАС представляет собой оператор преобразования Ганкеля нулевого порядка.
Расширение до веерной или конической балки CT
Теорема о проекции среза подходит для реконструкции КТ-изображения с параллельными проекциями луча. Это не относится напрямую к ТТ с веерным или конусным лучом. Теорема была распространена на реконструкцию КТ изображений веерного и конусообразного пучков Шуанг-жэнь Чжао в 1995 году.[3]
Смотрите также
Рекомендации
- ^ Брейсуэлл, Рональд Н. (1956). «Полосовая интеграция в радиоастрономии». Австралийский журнал физики. 9 (2): 198–217. Bibcode:1956AuJPh ... 9..198B. Дои:10.1071 / PH560198.
- ^ Нг, Рен (2005). "Фотография среза Фурье" (PDF). Транзакции ACM на графике. 24 (3): 735–744. Дои:10.1145/1073204.1073256.
- ^ Чжао С.Р. и Х. Холлинг (1995). Новый метод преобразования Фурье для веерной томографии. Опубликовано в 1995 г. Отчет о симпозиуме по ядерной науке и конференции по медицинской визуализации. 2. С. 1287–91. Дои:10.1109 / NSSMIC.1995.510494. ISBN 978-0-7803-3180-8.
дальнейшее чтение
- Брейсуэлл, Рональд Н. (1990). «Числовые преобразования». Наука. 248 (4956): 697–704. Bibcode:1990Sci ... 248..697B. Дои:10.1126 / science.248.4956.697. PMID 17812072.
- Брейсуэлл, Рональд Н. (1956). "Интеграция полос в радиоастрономии". Aust. J. Phys. 9 (2): 198. Bibcode:1956AuJPh ... 9..198B. Дои:10.1071 / PH560198.
- Гаскилл, Джек Д. (2005). Линейные системы, преобразования Фурье и оптика. John Wiley & Sons, Нью-Йорк. ISBN 978-0-471-29288-3.
- Нг, Рен (2005). "Фотография среза Фурье" (PDF). Транзакции ACM на графике. 24 (3): 735–744. Дои:10.1145/1073204.1073256.
- Чжао, Шуанг-Рен; Холлинг, Хорст (1995). «Реконструкция проекций конического пучка со свободным трактом источника обобщенным методом Фурье». Материалы международного совещания 1995 г. по восстановлению полностью трехмерного изображения в радиологии и ядерной медицине: 323–7.
- Garces, Daissy H .; Родос, Уильям Т .; Пенья, Нестор (2011). "Теорема о проекции-срезе: компактное обозначение". Журнал Оптического общества Америки A. 28 (5): 766–769. Bibcode:2011JOSAA..28..766G. Дои:10.1364 / JOSAA.28.000766. PMID 21532686.
внешняя ссылка
- Теорема Фурье-среза (видео). Часть курса «Компьютерная томография и ASTRA Toolbox». Университет Антверпена. 10 сентября 2015 года.









![= int _ {- infty} ^ { infty} left [ int _ {- infty} ^ { infty} f (x, y) , dy right] , e ^ {- 2 пи ixk_ {x}} dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d83ac57cdc5698f37cff3d7535c27bd32fef52)

