WikiDer > Проективная ортогональная группа
В проективная геометрия и линейная алгебра, то проективная ортогональная группа PO - индуцированный действие из ортогональная группа из квадратичное пространство V = (V,Q)[примечание 1] на связанных проективное пространство П(V). Явно проективно ортогональная группа - это факторгруппа
- PO (V) = O (V) / ZO (V) = O (V)/{±я}
где O (V) - ортогональная группа к (V) и ZO (V)={±я} - подгруппа всех ортогональных скалярные преобразования из V - они состоят из идентичности и отражение через начало координат. Эти скаляры выделены, потому что они действуют тривиально на проективном пространстве и образуют ядро действия, а обозначение "Z" связано с тем, что скалярные преобразования являются центр ортогональной группы.
В проективная специальная ортогональная группа, PSO, определяется аналогично, как индуцированное действие специальная ортогональная группа на ассоциированном проективном пространстве. Ясно:
- PSO (V) = SO (V) / ZSO (V)
где SO (V) - специальная ортогональная группа над V и ЗСО (V) - подгруппа ортогональных скалярных преобразований с единицей детерминант. Здесь ZSO является центром SO и является тривиальным в нечетной размерности, в то время как в четной размерности он равен {± 1} - это нечетное / четное различие происходит во всей структуре ортогональных групп. По аналогии с GL / SL и GO / SO проективную ортогональную группу также иногда называют проективный Общее ортогональная группа и обозначается PGO.
Подобно ортогональной группе, проективная ортогональная группа может быть определена над любым полем и с различными квадратичными формами, хотя, как и в случае с обычной ортогональной группой, основной упор делается на настоящий положительно определенный проективная ортогональная группа; другие области разработаны в обобщения, ниже. Если не указано иное, в дальнейшем PO и PSO будут относиться к реальным положительно определенным группам.
Словно спиновые группы и группы контактов, которые являются покрытиями, а не факторами (специальных) ортогональных групп, проективные (специальные) ортогональные группы представляют интерес для (проективных) геометрических аналогов евклидовой геометрии, поскольку связаны Группы Ли, И в теория представлений.
По сути, (действительная положительно определенная) проективная ортогональная группа PO может быть определена как изометрии из реальное проективное пространство, а PSO можно определить как сохраняющий ориентацию изометрии реального проективного пространства (когда пространство ориентируемо; иначе PSO = PO).
Структура
Нечетные и четные размеры
Структура PO значительно отличается между нечетным и четным размером, в основном потому, что в четном измерении отражение через начало координат сохраняет ориентацию, а в нечетном измерении меняет ориентацию ( но ). Это видно в том факте, что каждое нечетномерное реальное проективное пространство ориентируемо, в то время как каждое четномерное реальное проективное пространство положительной размерности неориентируемо. На более абстрактном уровне Алгебры Ли нечетных и четномерных проективных ортогональных групп образуют два разных семейства:
Таким образом, [заметка 2]пока и вместо этого нетривиальный центральное расширение ПО (2k).
Остерегайтесь этого PO (2k+1) - изометрии а ПО (2k) - изометрии - нечетномерная (векторная) группа - это изометрии четномерного проективного пространства, а четномерная (векторная) группа - это изометрии нечетномерного проективного пространства.
В нечетном измерении [заметка 3] так что группу проективных изометрий можно отождествить с группой изометрий вращения.
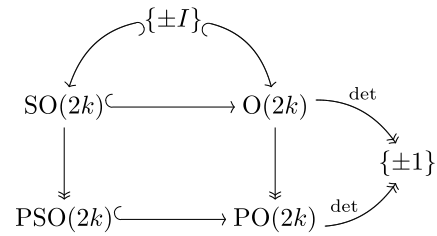
В четном измерении SO (2k) → PSO (2k) и O (2k) → PO (2k) являются перекрытиями 2 к 1, а PSO (2k)
Общие свойства
PSO и PO являются бесцентровый, как с PSL и PGL; это потому, что скалярные матрицы являются не только центром SO и O, но и гиперцентр (частное по центру не всегда дает бесцентровую группу).
PSO - это максимальная компактная подгруппа в проективная специальная линейная группа PSL, а PO максимально компактна в проективная общая линейная группа PGL. Это аналогично тому, что SO максимально компактно в SL, а O максимально компактно в GL.
Теория представлений
PO представляет основной интерес в теории представлений: гомоморфизм групп грамм → PGL называется проективное представление из ГРАММ, так же, как отображение G → GL называется линейное представление группы G, и, как любое линейное представление, можно свести к отображению грамм → O (взяв инвариантное внутреннее произведение), любое проективное представление может быть сведено к отображению грамм → ПО.
Видеть проективная линейная группа: теория представлений для дальнейшего обсуждения.
Подгруппы
Подгруппы проективной ортогональной группы соответствуют подгруппам ортогональной группы, которые содержат (который имеет центральная симметрия). Как всегда с факторной картой ( решеточная теорема), Существует Связь Галуа между подгруппами O и PO, где присоединение к O (полученное путем взятия изображения в PO, а затем прообраза в O) просто добавляет если отсутствует.
Особый интерес представляют дискретные подгруппы, которые могут быть реализованы как симметрии проективные многогранники - они соответствуют (дискретным) точечным группам, которые включают центральную симметрию. Сравнить с дискретные подгруппы группы Spin, в частности, трехмерный случай бинарные полиэдральные группы.
Например, в 3-х измерениях 4 из 5 Платоновы тела имеют центральную симметрию (куб / октаэдр, додекаэдр / икосаэдр), в то время как тетраэдр нет - однако звездчатый октаэдр имеет центральную симметрию, хотя результирующая группа симметрии такая же, как у куба / октаэдра.
Топология
PO и PSO, как бесцентровые топологические группы, находятся в нижней части последовательности группы покрытия, вершиной которого являются (односвязный) Группы контактов или же Спиновая группа, соответственно:
- Штырь±(п) → O (п) → PO (п).
- Вращение(п) → SO (п) → PSO (п).
Все эти группы компактные реальные формы той же алгебры Ли.
Это все покрытия 2 к 1, кроме SO (2k+1) → PSO (2k+1), который равен 1 к 1 (изоморфизм).
Гомотопические группы
Гомотопические группы над не меняются под крышками, поэтому они согласуются с покрытиями ортогональной группы. Нижние гомотопические группы задаются следующим образом.
Фундаментальная группа (бесцентровых) ПСО (п) равен центру (односвязного) Spin (п), что всегда верно для покрывающих групп:
С использованием таблица центров спиновых групп дает (для ):
В малых габаритах:
- поскольку группа тривиальна.
- поскольку это топологически круг, однако обратите внимание, что прообраз тождества в Spin (2) является что касается других
Группы гомологий
Этот раздел пуст. Вы можете помочь добавляя к этому. (Май 2010 г.) |
Связки
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Май 2010 г.) |
Так же, как ортогональная группа структурная группа из векторные пакеты, проективная ортогональная группа является структурной группой проективные пучки, а соответствующие классификация пространства обозначается BPO.
Обобщения
Как и в случае с ортогональной группой, проективную ортогональную группу можно обобщить двумя основными способами: изменить поле или изменить квадратичную форму. Помимо действительных чисел, основной интерес представляют комплексные числа или конечные поля, в то время как (по действительным числам) квадратичные формы также могут быть неопределенные формы, и обозначаются PO (п,q) своей подписью.
Комплексная проективно ортогональная группа PO (п,C) не следует путать с проективная унитарная группа, ПУ (п): PO сохраняет симметричную форму, а PU сохраняет эрмитская форма - PU - симметрии комплексного проективного пространства (сохраняющие Метрика Фубини – Этюд).
В полях характеристики 2 добавляются сложности: квадратичные формы и симметричные билинейные формы больше не эквивалентны, а определитель необходимо заменить на Инвариант Диксона.
Конечные поля
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Май 2010 г.) |
Проективная ортогональная группа над конечным полем используется при построении семейства конечных простые группы из Тип лжи, а именно Группы Шевалле типа Dп. Ортогональная группа над конечным полем O (п,q) непросто, так как в нем SO как подгруппа и нетривиальный центр ({±я}) (следовательно, PO как частное). Они оба фиксируются переходом к PSO, но сам PSO в целом не прост, и вместо этого нужно использовать подгруппу (которая может иметь индекс 1 или 2), определенную спинорная норма (в нечетной характеристике) или квазидетерминант (в четной характеристике).[1] Квазидетерминант можно определить как куда D это Инвариант Диксона (это определитель, определяемый инвариантом Диксона), или в терминах размерности фиксированного пространства.
Примечания
- ^ Квадратичное пространство - это векторное пространство V вместе с квадратичная форма Q; в Q опускается из обозначений, когда он ясен.
- ^ Этот продукт внутренняя прямая сумма - продукт подгрупп, а не просто абстрактный внешняя прямая сумма.
- ^ В изоморфизм/ равенство различие в этом уравнении связано с тем, что контекст представляет собой карту отношений 2 к 1 - ПСО (2k+1) и ПО (2k+1) являются равными подмножествами цели (а именно всего пространства), следовательно, равенство, а индуцированное отображение является изоморфизмом, но две группы являются подмножествами разных пространств, следовательно, это изоморфизм, а не равенство. Видеть (Конвей и Смит 2003, п. 34) в качестве примера проводимого различия.
Смотрите также
Рекомендации
Эта статья нужны дополнительные цитаты для проверка. (Май 2010 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
- Конвей, Джон Хортон; Смит, Дерек Алан (07.02.2003), "3.7 Проективные или эллиптические группы", О кватернионах и октонионах, A. K Peters, Ltd., стр.34, ISBN 978-1-56881-134-5
- Conway, J. H .; Curtis, R.T .; Norton, S.P .; Паркер, Р. А .; и Уилсон, Р. А. «Группы GO_n (q), SO_n (q), PGO_n (q) и PSO_n (q), и O_n (q)». §2.4 в Атласе конечных групп: максимальные подгруппы и обыкновенные характеры для простых групп. Оксфорд, Англия: Clarendon Press, стр. Xi – xii, 1985.