WikiDer > Квантовое возрождение

В квантовая механика, то квантовое возрождение [1]является периодическим повторением квантовой волновая функцияот его первоначальной формы во время эволюции во времени либо много раз в пространстве в виде многократных масштабированных дробей в форме начальной волновой функции (дробное возрождение), либо приблизительно или точно до его первоначальной формы с самого начала (полное возрождение). Таким образом, периодическая во времени квантовая волновая функция демонстрирует полное возрождение каждые период. Явление возрождений наиболее легко наблюдать при волновых функциях хорошо локализован волновые пакеты в начале временной эволюции, например, в атоме водорода. Для водорода дробные возрождения проявляются как множественные угловые гауссовы выпуклости вокруг круга, нарисованного радиальным максимумом ведущего круговое состояние составляющая (имеющая наибольшую амплитуду в расширении собственного состояния) исходного локализованного состояния и полное возрождение в качестве исходного гауссовского.[2]Полные пробуждения точны для бесконечная квантовая яма, гармонический осциллятор или атом водорода, а для более коротких времен являются приблизительными для атома водорода и многих квантовых систем.[3]
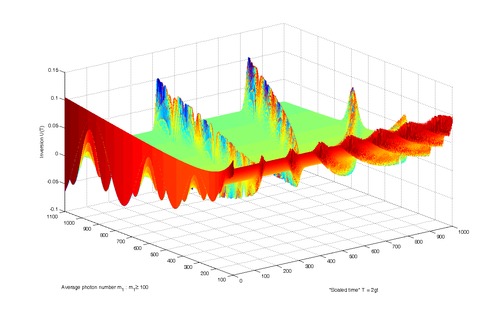
Сюжет коллапсов и возрождений квантовых колебаний атомной инверсии JCM.[4]
Пример - произвольная усеченная волновая функция квантовой системы с рациональными энергиями.
Рассмотрим квантовую систему с энергиями и собственные состояния
и пусть энергии будут рациональный доли некоторой постоянной
(например для атом водорода , , .
Затем усеченный (до состояний) решение зависящего от времени уравнения Шредингера имеет вид
.
Позволять быть к наименьшее общее кратное из всех и наибольший общий делитель из всех затем для каждого то целое число, для каждого то целое число, является полным кратным угол и
после полного времени возрождения
- .
Для такой маленькой квантовой системы, как водород и Всего за 100 человек может пройти квадриллионы лет, прежде чем он полностью возродится. Особенно после того, как созданные поля Троянский волновой пакет в атоме водорода существует без каких-либо внешних полейстробоскопически и вечно повторяется после охвата почти всего гиперкуба квантовых фаз ровно каждый период полного возрождения.
Поразительное следствие состоит в том, что никакой конечный разрядный компьютер не может точно воспроизвести числовую волновую функцию в течение сколь угодно долгого времени. Если номер процессора n-кусочек длинный плавающая точка число, то число может быть сохранено компьютером только с конечной точностью после запятой, а энергия (до 8 цифр после запятой), например, 2.34576893 = 234576893/100000000 и как конечная дробь это точно рационально и полное возрождение возникает для любой волновой функции любой квантовой системы после времени который является его максимальным показателем, и так далее, это может не быть верным для всех квантовых систем, или все стационарные квантовые системы претерпевают полное и точное численное возрождение.
В системе с рациональными энергиями, т.е. там, где существует квантовое точное полное возрождение, его существование немедленно доказывает квантовое Теорема Пуанкаре о возвращении а время полного квантового возрождения равно времени возврата Пуанкаре. В то время как рациональные числа плотный в действительных числах, а произвольная функция квантового числа может быть аппроксимирована произвольно точно с помощью Аппроксимации Паде поэтому с коэффициентами произвольной десятичной точности на сколь угодно долгое время каждая квантовая система почти точно оживает. Это также означает, что возвращение Пуанкаре и полное возрождение математически одно и то же. [5] и обычно считается, что повторение называется полным возрождением, если оно происходит по прошествии разумного и физически измеримого времени, которое может быть обнаружено реалистичным устройством, и это происходит из-за очень особого энергетического спектра, имеющего большой базовый энергетический зазор. энергии которых кратны произвольным (не обязательно гармоническим) значениям.
Рекомендации
- ^ J.H. Эберли; N.B. Нарожный и Дж. Санчес-Мондрагон (1980). «Периодический спонтанный коллапс и возрождение в простой квантовой модели». Phys. Rev. Lett. 44 (20): 1323–1326. Bibcode:1980PhRvL..44.1323E. Дои:10.1103 / PhysRevLett.44.1323.
- ^ З. Дачич Гаэта и К. Р. Страуд младший (1990). «Классическая и квантово-механическая динамика квазиклассического состояния атома водорода». Phys. Ред. А. 42 (11): 6308–6313. Bibcode:1990ПхРва..42.6308Г. Дои:10.1103 / PhysRevA.42.6308.
- ^ Чжан, Цзян-Минь; Хак, Масудул (2014). «Негладкая динамика с разрешением по уровням, проиллюстрированная периодически управляемой моделью жесткого связывания». arXiv:1404.4280.
- ^ А.А. Карацуба; Э. А. Карацуба (2009). «Формула пересуммирования коллапса и возрождения в модели Джейнса-Каммингса». J. Phys. A: Математика. Теор. 42: 195304, 16. Bibcode:2009JPhA ... 42s5304K. Дои:10.1088/1751-8113/42/19/195304.
- ^ Bocchieri, P .; Loinger, A. (1957). «Квантовая теорема о возвращаемости». Phys. Ред. 107 (2): 337–338. Bibcode:1957ПхРв..107..337Б. Дои:10.1103 / PhysRev.107.337.