WikiDer > Квантовая спиновая жидкость

Quantum spin liquid

В физика конденсированного состояния, а квантовая спиновая жидкость это фаза материи которые могут быть сформированы путем взаимодействия квантовые спины в некоторых магнитных материалах. Квантовые спиновые жидкости (КСЛ) обычно характеризуются своим дальнодействием. квантовая запутанность, дробный возбуждения, и отсутствие обычных магнитных порядок.[1]

Состояние квантовой спиновой жидкости было впервые предложено физиком Фил Андерсон в 1973 г. в качестве основного состояния системы спинов на треугольная решетка которые взаимодействуют антиферромагнитно со своими ближайшими соседями; т.е. соседние спины стремятся выровняться в противоположных направлениях.[2] Квантовые спиновые жидкости вызвали дополнительный интерес, когда в 1987 году Андерсон предложил теорию, описывающую высокотемпературная сверхпроводимость в терминах неупорядоченного спин-жидкостного состояния.[3][4]

Основные свойства

Самый простой вид магнитной фазы - это парамагнетик, где каждый отдельный спин ведет себя независимо от остальных, как атомы в идеальный газ. Эта сильно разупорядоченная фаза является типичным состоянием магнитов при высоких температурах, где преобладают тепловые флуктуации. После охлаждения спины часто попадают в ферромагнетик (или же антиферромагнетик) фаза. На этом этапе взаимодействия между спинами заставляют их выстраиваться в крупномасштабные паттерны, такие как домены, полосы или шахматные доски. Эти структуры дальнего действия называются «магнитным порядком» и аналогичны регулярной кристаллической структуре, образованной многими твердыми телами.[5]

Квантовые спиновые жидкости предлагают драматическую альтернативу этому типичному поведению. Одно интуитивное описание этого состояния - «жидкость» беспорядочный спины, по сравнению с ферромагнитный состояние вращения,[6] во многом жидкая вода находится в неупорядоченном состоянии по сравнению с кристаллическим льдом. Однако, в отличие от других неупорядоченных состояний, состояние квантовой спиновой жидкости сохраняет свой беспорядок до очень низких температур.[7] Более современная характеристика квантовых спиновых жидкостей включает их топологический порядок,[8] дальний квантовая запутанность характеристики,[1] и анйон возбуждения.[9]

Примеры

Некоторые физические модели имеют неупорядоченное основное состояние, которое можно описать как квантовую спиновую жидкость.

Разочарованные магнитные моменты

Разочарованный Изинг вращается на треугольнике.

Локализованные спины расстроенный если существуют конкурирующие обменные взаимодействия, которые не могут быть выполнены одновременно, что приводит к большому вырождению основного состояния системы. Треугольник Изинг спины (это означает, что единственная возможная ориентация спинов - «вверх» или «вниз»), которые взаимодействуют антиферромагнитно, является простым примером разочарования. В основном состоянии два спина могут быть антипараллельными, а третий - нет. Это приводит к увеличению возможных ориентаций (в данном случае шести) спинов в основном состоянии, усиливая флуктуации и тем самым подавляя магнитное упорядочение.

Резонирующие валентные связи (RVB)

Основная статья: Теория резонирующей валентной связи
Валентная связь прочная. Связи образуют определенный узор и состоят из пар перепутанных спинов.

Чтобы построить основное состояние без магнитного момента, можно использовать состояния валентной связи, где два электронных спина образуют синглет со спином 0 из-за антиферромагнитного взаимодействия. Если каждый спин в системе связан таким образом, состояние системы в целом тоже имеет спин 0 и не является магнитным. Два спина, образующие связь, максимально запутанный, при этом не перепутаны с другими спинами. Если все спины распределены между определенными локализованными статическими связями, это называется валентная связь твердое тело (VBS).

Есть две вещи, которые по-прежнему отличают VBS от спиновой жидкости: во-первых, из-за упорядочения связей определенным образом симметрия решетки обычно нарушается, что не относится к спиновой жидкости. Во-вторых, в этом основном состоянии отсутствует дальнодействующая запутанность. Чтобы достичь этого, необходимо разрешить квантово-механические флуктуации валентных связей, ведущие к основному состоянию, состоящему из суперпозиции множества различных разбиений спинов на валентные связи. Если разделения распределены одинаково (с одинаковой квантовой амплитудой), нет никакого предпочтения для какого-либо конкретного разделения («жидкость с валентными связями»). Такой вид волновой функции основного состояния был предложен П. В. Андерсон в 1973 г. как основное состояние спиновых жидкостей[2] и называется резонирующая валентная связь (RVB) состояние. Эти состояния представляют большой теоретический интерес, поскольку предполагается, что они играют ключевую роль в физике высокотемпературных сверхпроводников.[4]

  • Одна возможная пара спинов на короткое время в состоянии RVB.

  • Дальнейшее спаривание спинов.

Возбуждения

Спинон движется в спиновых жидкостях.

Валентные связи не обязательно должны образовываться только ближайшими соседями, и их распределение может различаться в разных материалах. Основные состояния с большим вкладом длинных валентных связей имеют больше низкоэнергетических спиновых возбуждений, так как эти валентные связи легче разрушить. При разбивании они образуют два бесплатных спина. Другие возбуждения перестраивают валентные связи, приводя к низкоэнергетическим возбуждениям даже для короткодействующих связей. Особенностью спиновых жидкостей является то, что они поддерживают экзотические возбуждения, имея в виду возбуждения с дробными квантовыми числами. Ярким примером является возбуждение спиноны которые нейтральны по заряду и несут спин В спиновых жидкостях спинон создается, если один спин не спарен по валентной связи. Он может двигаться, перестраивая близлежащие валентные связи при низких затратах энергии.

Реализации (стабильных) состояний РВБ

Первое обсуждение состояния RVB на квадратной решетке с использованием изображения RVB[10] рассматривают только связи ближайших соседей, которые соединяют разные подрешетки. Построенное состояние RVB представляет собой суперпозицию с равной амплитудой всех конфигураций связей ближайших соседей. Считается, что такое состояние RVB содержит возникающие беззазорные калибровочное поле, которое может ограничивать спиноны и т. д. Таким образом, состояние RVB ближайших соседей с одинаковой амплитудой на квадратной решетке нестабильно и не соответствует фазе квантового спина. Он может описывать критическую точку фазового перехода между двумя стабильными фазами. Вариант состояния RVB, который является стабильным и содержит деконфайндерные спиноны, является состоянием кирального спина.[11][12] Позже был предложен другой вариант стабильного состояния RVB с деконфайнерами спинонов - спиновая жидкость Z2: [13] [14] который реализует простейший топологический порядок – Z2 топологический порядок. И киральное спиновое состояние, и спиновое жидкое состояние Z2 имеют длинные связи RVB, которые соединяют одну и ту же подрешетку. В состоянии кирального спина разные конфигурации связей могут иметь комплексные амплитуды, в то время как в состоянии спиновой жидкости Z2 разные конфигурации связей имеют только реальные амплитуды. Состояние RVB на треугольной решетке также реализует спиновую жидкость Z2,[15] где разные конфигурации связей имеют только реальные амплитуды. Модель торического кода - еще одна реализация спиновой жидкости Z2 (и Z2 топологический порядок), которая явно нарушает симметрию вращения спина и является точно разрешимой.[16]

Экспериментальные сигнатуры и зонды

Поскольку не существует единого экспериментального признака, который идентифицирует материал как спиновую жидкость, необходимо провести несколько экспериментов, чтобы получить информацию о различных свойствах, характеризующих спиновую жидкость. [17]

Магнитная восприимчивость

В высокотемпературном, классическом парамагнетик фаза, магнитная восприимчивость дается Закон Кюри – Вейсса

Подгонка экспериментальных данных к этому уравнению определяет феноменологическую температуру Кюри – Вейсса, . Есть вторая температура, , где в материале начинает развиваться магнитный порядок, о чем свидетельствует неаналитический особенность в . Их соотношение называется параметр разочарования

В классическом антиферромангете две температуры должны совпадать и давать . Идеальная квантовая спиновая жидкость не будет развивать магнитный порядок ни при какой температуре и поэтому будет расходящийся параметр разочарования .[18] Большое значение поэтому является хорошим показателем возможной прядильной жидкой фазы. Некоторые фрустрированные материалы с разной структурой решетки и их Температура Кюри – Вейсса перечислены в таблице ниже.[7] Все они являются кандидатами на спиновые жидкости.

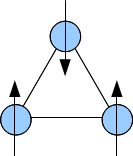
МатериалРешетка
κ- (BEDT-TTF)2Cu2(CN)3анизотропный треугольник-375
ZnCu3(ОЙ)6Cl2 (гербертсмитит)Кагоме-241
BaCu3V2О8(ОЙ)2 (везигний)Кагоме
Na4Ir3О8Гиперкагоме-650
PbCuTe2О6Гиперкагоме-22 [19]
Cu- (1,3-бензолдикарбоксилат)Кагоме-33 [20]
Руб.2Cu3SnF12Кагоме[21]
1T-TaS2Треугольный

Другой

Одно из самых прямых доказательств отсутствия магнитного упорядочения дает ЯМР или же μSR эксперименты. Если присутствует локальное магнитное поле, это может повлиять на спин ядра или мюона, который можно измерить. 1ЧАС-ЯМР измерения [22] на κ- (BEDT-TTF)2Cu2(CN)3 не показали признаков магнитного упорядочения вплоть до 32 мК, что на четыре порядка меньше, чем константа связи J≈250 К[23] между соседними спинами в этом соединении. Дальнейшие исследования включают:

  • Измерения удельной теплоемкости дают информацию о низкоэнергетической плотности состояний, которую можно сравнить с теоретическими моделями.
  • Измерения теплового переноса может определить, являются ли возбуждения локальными или странствующими.
  • Рассеяние нейтронов дает информацию о природе возбуждений и корреляций (например, спиноны).
  • Измерения отражения может раскрыть спиноны, которые через возникающие калибровочные поля связываются с электромагнитным полем, создавая степенную оптическую проводимость.[24]
Гербертсмитит, минерал, основное состояние которого, как было показано, имеет QSL-поведение

Кандидатские материалы

Тип РВБ

Измерения нейтронного рассеяния хлоркупрата цезия Cs2CuCl4, антиферромагнетик со спином 1/2 на треугольной решетке, обнаружил диффузное рассеяние. Это было приписано спинонам, возникающим из состояния 2D RVB.[25] Более поздние теоретические работы поставили под сомнение эту картину, утверждая, что все экспериментальные результаты были следствием одномерных спинонов, ограниченных отдельными цепочками.[26]

Впоследствии это наблюдалось в органическом изоляторе Мотта (κ- (BEDT-TTF)2Cu2(CN)3) группой Каноды в 2003 году.[22] Это может соответствовать бесщелевой спиновой жидкости со спинонной поверхностью Ферми (так называемое однородное состояние RVB).[2] Своеобразная фазовая диаграмма этого органического соединения квантовой спиновой жидкости была впервые тщательно составлена ​​с использованием мюонная спиновая спектроскопия.[27]

Гербертсмитит

Гербертсмитит является одним из наиболее изученных материалов-кандидатов на QSL.[18] Это минерал с химическим составом ZnCu.3(ОЙ)6Cl2 и ромбоэдрический Кристальная структура. Примечательно, что ионы меди в этой структуре образуют сложенные двухмерные слои решетки кагоме. Кроме того, суперобмен по кислородным связям создает сильное антиферромагнитное взаимодействие между медь вращается внутри одного слоя, тогда как связь между слоями незначительна.[18] Следовательно, это хорошая реализация антиферромагнитной модели Гейзенберга со спином 1/2 на решетке кагоме, которая является прототипическим теоретическим примером квантовой спиновой жидкости.[28][29]

Впервые о синтетическом поликристаллическом порошке гербертсмитита было сообщено в 2005 году, и первоначальные исследования магнитной восприимчивости не показали никаких признаков магнитного порядка вплоть до 2К.[30] В последующем исследовании было подтверждено отсутствие магнитного порядка вплоть до 50 мК, неупругое рассеяние нейтронов измерения показали широкий спектр низкоэнергетических спиновых возбуждений, а измерения удельной теплоемкости при низких температурах имели степенное масштабирование. Это дало убедительные доказательства наличия состояния спиновой жидкости с бесщелевой крутиться возбуждения.[31] Широкий спектр дополнительных экспериментов, включая 17О ЯМР,[32] и нейтронная спектроскопия коэффициент динамической магнитной структуры,[33] подтвердили идентификацию гербертсмитита как бесщелевого спинового жидкого материала, хотя точная характеристика оставалась неясной по состоянию на 2010 год.[34]

В 2011 г. были выращены и охарактеризованы крупные (миллиметровые) монокристаллы гербертсмитита.[35] Это позволило более точно измерить возможные свойства спиновой жидкости. В частности, эксперименты по неупругому рассеянию нейтронов с импульсным разрешением показали широкий спектр возбуждений. Это было интерпретировано как свидетельство существования бесщелевых фракционированных спинонов.[36] Последующие эксперименты (с использованием 17О ЯМР и рассеяние нейтронов низкой энергии с высоким разрешением) уточнили эту картину и определили, что на самом деле существует небольшая щель возбуждения спинонов 0,07-0,09 мэВ.[37][38]

Некоторые измерения наводили на мысль о квантово-критический поведение.[39] Магнитный отклик этого материала отображает масштабное соотношение в объемном переменном токе. восприимчивость и низкоэнергетическая динамическая восприимчивость, при этом низкотемпературная теплоемкость сильно зависит от магнитного поля.[40][41] Это масштабирование наблюдается в определенных квантовых антиферромагнетики, металлы с тяжелыми фермионами, и двумерный 3Он как признак близости к квантовой критической точке.[42]

В 2020 г. монодисперсный монокристалл наночастицы гербертсмитита (~ 10 нм) были синтезированы при комнатной температуре с использованием газодиффузионная электрокристаллизация, показывая, что их спин-жидкостная природа сохраняется при таких малых размерах.[43]

Рис.1: T-зависимость электронной теплоемкости C / T YbRh2Si2 при разных магнитных полях [44] как показано в легенде. Значения (C / T)Максимум и тМаксимум при B = 8 Тесла. Максимальный (C / T)Максимум уменьшается с ростом магнитного поля B, а TМаксимум сдвигается в сторону более высоких Т, достигая 14 К при В = 18 Тесла. Замечая, что C / T ~ χ ~ M *, заключаем, что SCQSL в ZnCu3(ОЙ)6Cl2 2 показывает поведение, подобное тяжелым фермионам в YbRh2Si2.
Рис.2: T-зависимость магнитной восприимчивости χ при различных магнитных полях для ZnCu3(ОЙ)6Cl2.[40] Значения χМаксимум и тМаксимум при B = 7 Тесла. T-зависимость T(-2/3) при B = 0 изображен сплошной кривой. Максимум χМаксимум(T) уменьшается с ростом магнитного поля B, а TМаксимум(B) сдвигается к более высокой температуре, достигающей 15 К при B = 14 Тесла. Наблюдая, что χ ~ C / T ~ M *, можно заключить, что теплоемкость YbRh2Si2 показанный на рис. 1, показывает поведение, подобное χ. Таким образом, SCQSL в ZnCu3(ОЙ)6Cl2 ведет себя как тяжелые фермионы в YbRh2Si2.[45]

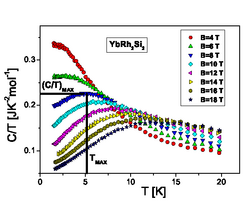
Он может реализовывать спиновую жидкость U (1) -Дирака.[46]

Китаев спиновые жидкости

Еще одно свидетельство существования квантовой спиновой жидкости было обнаружено в двумерном материале в августе 2015 года. Национальная лаборатория Окриджав сотрудничестве с физиками из Кембриджского университета и Институтом физики сложных систем Макса Планка в Дрездене, Германия, измерили первые сигнатуры этих дробных частиц, известных как Майорана фермионы, в двумерном материале со структурой, подобной графен. Их экспериментальные результаты успешно согласуются с одной из основных теоретических моделей квантовой спиновой жидкости, известной как Сотовая модель Китаева.[47] [48]

Тип кагоме

Ca10Cr7О28 разочарован Кагоме двухслойный магнит, который не развивает дальний порядок даже ниже 1 К и имеет размытый спектр бесщелевых возбуждений. [49]

Сильно коррелированная квантовая спиновая жидкость

В сильно коррелированная квантовая спиновая жидкость (SCQSL) - конкретная реализация возможного квантовая спиновая жидкость (QSL)[7] [39] представляющий новый тип сильно коррелированных электрических изолятор (SCI), который обладает свойствами тяжелый фермион металлов за одним исключением: он сопротивляется потоку электрический заряд. [45] [50] При низких температурах Т то удельная теплоемкость этого типа изолятора пропорциональна Тп, с п меньше или равно 1, а не п= 3, как и должно быть в случае обычного изолятора, у которого теплоемкость пропорционально Т3. Когда магнитное поле B применяется к SCI, удельная теплоемкость сильно зависит от B, в отличие от обычных изоляторов. Есть несколько кандидатов SCI; наиболее перспективным среди них является Гербертсмитит,[50] а минеральная с химической структурой ZnCu3(ОЙ)6Cl2.

Особые свойства: Топологический фермионная конденсация квантовый фазовый переход

Экспериментальные факты, собранные на тяжелый фермион (HF) металлы и двумерный Гелий-3 продемонстрировать, что квазичастица эффективная масса M* очень большой или даже расходится. Топологический фермионная конденсация квантовый фазовый переход (FCQPT) сохраняет квазичастицы, и образует плоскую диапазон энергии на Уровень Ферми. Появление FCQPT напрямую связано с неограниченным ростом эффективная масса M*.[42] Вблизи FCQPT M * начинает зависеть от температура Т, числовая плотность Икс, магнитное поле B и другие внешние параметры, такие как давление пи др. В отличие от Ландо парадигма, основанная на предположении, что эффективная масса приблизительно постоянна, в теории FCQPT эффективная масса новых квазичастиц сильно зависит от Т, Икс, B и т.д. Следовательно, чтобы согласиться / объяснить многочисленные экспериментальные факты, необходимо ввести расширенную парадигму квазичастиц, основанную на FCQPT. Главное здесь то, что четко определенные квазичастицы определяют термодинамический, расслабление, масштабирование и транспорт свойств сильно коррелированных ферми-систем и M * становится функцией Т, Икс, B, пи т. д. Данные, собранные для очень разных сильно коррелированных ферми-систем, демонстрируют универсальное масштабное поведение; другими словами, различные материалы с сильно коррелированными фермионами неожиданно оказываются однородными, образуя новый состояние дела состоящий из HF металлы, квазикристаллы, квантовая спиновая жидкость, двумерный Гелий-3, и соединения экспонирование высокотемпературная сверхпроводимость.[39][42]

Приложения

Материалы, поддерживающие квантовые спиновые состояния жидкости, могут найти применение в хранении данных и памяти. [51] В частности, можно реализовать топологические квантовые вычисления с помощью спин-жидкостных состояний.[52] Развитие квантовых спиновых жидкостей также может помочь в понимании высокотемпературная сверхпроводимость.[53]

Рекомендации

  1. ^ а б Savary, L .; Баленц, Л. (2017). «Квантовые спиновые жидкости: обзор». Отчеты о достижениях физики. 80 (1): 016502. arXiv:1601.03742. Bibcode:2017RPPh ... 80a6502S. Дои:10.1088/0034-4885/80/1/016502. PMID 27823986.
  2. ^ а б c П. В. Андерсон (1973). «Резонирующие валентные связи: новый вид изолятора?». Бюллетень материаловедения. 8 (2): 153–160. Дои:10.1016/0025-5408(73)90167-0.
  3. ^ Трафтон, Энн (28 марта 2011 г.). "Новый взгляд на сверхпроводимость?". Новости MIT. Получено 24 декабря 2012.
  4. ^ а б П. В. Андерсон (1987). "Резонирующее состояние валентной связи в La2CuO4 и сверхпроводимость ». Наука. 235 (4793): 1196–1198. Bibcode:1987Научный ... 235.1196A. Дои:10.1126 / science.235.4793.1196. PMID 17818979.
  5. ^ Чайкин, Пол М; Любенский, Том C (1995). Принципы физики конденсированного состояния. Пресса Кембриджского университета.
  6. ^ Уилкинс, Аласдер (15 августа 2011 г.). «Странное новое квантовое состояние материи: спиновые жидкости». io9. Получено 23 декабря 2012.
  7. ^ а б c Леон Баленц (2010). «Крутить жидкости в фрустрированных магнитах». Природа. 464 (7286): 199–208. Bibcode:2010Натура.464..199Б. Дои:10.1038 / природа08917. PMID 20220838.
  8. ^ Вулховер, Натали (2018-01-03). «Физики стремятся классифицировать все возможные фазы материи». Журнал Quanta. Получено 2019-05-05.
  9. ^ Вильчек, Франк (2017-02-28). "Внутри запутанного мира частиц Anyon". Журнал Quanta. Получено 2019-05-05.
  10. ^ Кивельсон, Стивен А .; Rokhsar, Daniel S .; Сетна, Джеймс П. (1987). «Топология резонирующего состояния валентной связи: солитоны и высокотемпературная сверхпроводимость». Физический обзор B. 35 (16): 8865. Bibcode:1987ПхРвБ..35.8865К. Дои:10.1103 / Physrevb.35.8865.
  11. ^ Kalmeyer, V .; Лафлин, Р. Б. (1987). «Эквивалентность резонирующей валентной связи и дробных квантовых холловских состояний». Письма с физическими проверками. 59 (18): 2095–2098. Bibcode:1987ПхРвЛ..59.2095К. Дои:10.1103 / Physrevlett.59.2095. PMID 10035416.
  12. ^ Вэнь Сяо-Ган; Wilczek, F .; Зи, А. (1989). «Киральные спиновые состояния и сверхпроводимость». Физический обзор B. 39 (16): 11413. Bibcode:1989PhRvB..3911413W. CiteSeerX 10.1.1.676.519. Дои:10.1103 / Physrevb.39.11413.
  13. ^ Читать, N .; Сачдев, Субир (1991). «Разложение при больших N для фрустрированных квантовых антиферромагнетиков». Письма с физическими проверками. 66 (13): 1773–1776. Bibcode:1991ПхРвЛ..66.1773Р. Дои:10.1103 / Physrevlett.66.1773. PMID 10043303.
  14. ^ Вэнь, Сяо-Ган (1991). "Теория среднего поля состояний спиновой жидкости с конечными энергетическими зазорами". Физический обзор B. 44 (6): 2664. Bibcode:1991PhRvB..44.2664W. Дои:10.1103 / Physrevb.44.2664. PMID 9999836.
  15. ^ Moessner, R .; Сонди, С. Л. (2002). "Физика жидкости с резонирующей валентной связью на треугольной решетке". Приложение "Прогресс теоретической физики". 145: 37–42. arXiv:cond-mat / 0205029. Bibcode:2002PThPS.145 ... 37M. Дои:10.1143 / PTPS.145.37.
  16. ^ Китаев, А.Ю .; Баленц, Леон (2003). «Отказоустойчивые квантовые вычисления анонимами». Анналы физики. 303 (1): 2–30. arXiv:Quant-ph / 9707021. Bibcode:2003AnPhy.303 .... 2K. Дои:10.1016 / S0003-4916 (02) 00018-0.
  17. ^ Нолле, Йоханнес; Месснер, Родерих (2019). «Полевое руководство по прядению жидкостей». Ежегодный обзор физики конденсированного состояния. 10: 451–472. arXiv:1804.02037. Bibcode:2019ARCMP..10..451K. Дои:10.1146 / annurev-conmatphys-031218-013401.
  18. ^ а б c Норман, М.Р. (2016). «Гербертсмитит и поиски квантовой спиновой жидкости». Обзоры современной физики. 88 (4): 041002. arXiv:1710.02991. Дои:10.1103 / RevModPhys.88.041002.
  19. ^ Phys. Rev. Lett. 116, 107203 (2016)
  20. ^ Нытко, Эмили А .; Helton, Joel S .; Мюллер, Питер; Ночера, Дэниел Г. (2008). «Структурно совершенный S = 1/2 металлорганический гибридный антиферромагнетик Кагоме». Журнал Американского химического общества. 130 (10): 2922–2923. Дои:10.1021 / ja709991u. PMID 18275194.
  21. ^ Matan, K .; Оно, Т .; Fukumoto, Y .; Sato, T. J .; и другие. (2010). «Вертушка твердого тела с валентной связью и триплетных возбуждений в двумерной деформированной решетке кагоме». Природа Физика. 6 (11): 865–869. arXiv:1007.3625. Bibcode:2010НатФ ... 6..865М. Дои:10.1038 / nphys1761.
  22. ^ а б Ю. Симидзу; К. Миягава; К. Канода; М. Маэсато; и другие. (2003). "Спиновое жидкое состояние в органическом изоляторе Мотта с треугольной решеткой". Письма с физическими проверками. 91 (10): 107001. arXiv:cond-mat / 0307483. Bibcode:2003PhRvL..91j7001S. Дои:10.1103 / PhysRevLett.91.107001. PMID 14525498.
  23. ^ В литературе значение J обычно указывается в единицах температуры () вместо энергии.
  24. ^ Т. Нг и П. А. Ли (2007). «Степенная проводимость внутри зазора Мотта: приложение к κ- (BEDT-TTF)2Cu2(CN)3". Письма с физическими проверками. 99 (15): 156402. arXiv:0706.0050. Bibcode:2007PhRvL..99o6402N. Дои:10.1103 / PhysRevLett.99.156402. PMID 17995193.
  25. ^ Coldea, R .; Tennant, D.A .; Цвелик, А.М .; Тылчинский, З. (12 февраля 2001 г.). «Экспериментальная реализация двумерной дробной квантовой спиновой жидкости». Письма с физическими проверками. 86 (7): 1335–1338. arXiv:cond-mat / 0007172. Bibcode:2001ПхРвЛ..86.1335С. Дои:10.1103 / PhysRevLett.86.1335. PMID 11178077. Отметим, что препринт был загружен в 2000 году.
  26. ^ Коно, Масанори; Старх Олег А; Баленц, Леон (2007). «Спиноны и триплоны в пространственно анизотропных фрустрированных антиферромагнетиках». Природа Физика. 3 (11): 790. arXiv:0706.2012. Bibcode:2007НатФ ... 3..790K. Дои:10.1038 / nphys749.
  27. ^ Pratt, F. L .; Бейкер, П. Дж .; Blundell, S.J .; Ланкастер, Т .; и другие. (2011). «Магнитная и немагнитная фазы квантовой спиновой жидкости». Природа. 471 (7340): 612–616. Bibcode:2011Натура.471..612П. Дои:10.1038 / природа09910. PMID 21455176.
  28. ^ Эльзер, Вейт (1989). «Ядерный антиферромагнетизм в зарегистрированном твердом теле 3He». Письма с физическими проверками. 62 (20): 2405–2408. Дои:10.1103 / PhysRevLett.62.2405. PMID 10039977.
  29. ^ Ян, Сименг и Хусе, Дэвид А. и Уайт, Стивен Р. (2011). "Спиновое жидкое основное состояние антиферромагнетика Гейзенберга S = 1/2". Наука. 332 (6034): 1173–1176. arXiv:1011.6114. Bibcode:2011Научный ... 332.1173Y. Дои:10.1126 / science.1201080.CS1 maint: использует параметр авторов (связь)
  30. ^ Шорс, Мэтью П.; Нытко, Эмили А; Бартлетт, Барт М; Ночера, Дэниел Дж. (2005). «Структурно совершенный антигерромагнетик Кагоме S = 1/2». Журнал Американского химического общества. 127 (39): 13462–13463. Дои:10.1021 / ja053891p. PMID 16190686.
  31. ^ Helton, J. S .; и другие. (2007). «Спиновая динамика решеточного антиферромагнетика Спин-1/2 ZnCu.3(ОЙ)6Cl2". Письма с физическими проверками. 98 (10): 107204. arXiv:cond-mat / 0610539. Bibcode:2007PhRvL..98j7204H. Дои:10.1103 / PhysRevLett.98.107204. PMID 17358563.
  32. ^ Olariu, A; и другие. (2008). "17О ЯМР-исследование внутренней магнитной восприимчивости и спиновой динамики квантового антиферромагнетика Кагоме ZnCu3(ОЙ)6Cl2". Письма с физическими проверками. 100 (9): 087202. arXiv:0711.2459. Дои:10.1103 / PhysRevLett.100.087202. PMID 18352658.
  33. ^ de Vries, M. A .; Стюарт, Дж. Р .; Deen, P.P .; Piatek, J.O .; Nilsen, G.J .; Ronnow, H.M .; Харрисон, А. (2009). «Безмасштабные антиферромагнитные флуктуации в гербертсмитите кагоме-антиферромагнетика S = 1/2». Письма с физическими проверками. 103 (23): 237201. arXiv:0902.3194. Bibcode:2009PhRvL.103w7201D. Дои:10.1103 / PhysRevLett.103.237201. ISSN 0031-9007. PMID 20366167.
  34. ^ Мендельс, Филипп; Берт, Фабрис (2010). «Квантовый антиферромагнетик Кагоме: ZnCu3(ОЙ)6Cl2". Журнал Физического общества Японии. 79 (1): 011001. arXiv:1001.0801. Bibcode:2010JPSJ ... 79a1001M. Дои:10.1143 / JPSJ.79.011001.
  35. ^ Хан, TH и Хелтон, Дж.С. и Чу, С. и Проди, Андреа и Сингх, Д.К. и Маццоли, Клаудио и М { "Иллер, П. и Ночера, Д.Г. и Ли, Янг С. (2011). «Синтез и характеристика монокристаллов кагоме-решетчатых антиферромагнетиков со спином 1/2 Zn.Икс Cu4-х(ОЙ)6Cl2" (PDF). Физический обзор B. 83 (10): 100402. Дои:10.1103 / PhysRevB.83.100402.CS1 maint: использует параметр авторов (связь)
  36. ^ Хан, Тиан-Хенг и Хелтон, Джоэл С. и Чу, Шаоян и Ночера, Даниэль Г. и Родригес-Ривера, Хосе А. и Брохольм, Коллин и Ли, Янг С. (2012). «Фракционированные возбуждения в спин-жидкостном состоянии антиферромагнетика на решетке кагоме». Природа. 492 (7429): 406–410. arXiv:1307.5047. Bibcode:2012Натура.492..406H. Дои:10.1038 / природа11659. PMID 23257883.CS1 maint: использует параметр авторов (связь)
  37. ^ Фу, Минсюань; Имаи, Такаши; Ли, Янг С. (2015). "Доказательства основного состояния спиновой жидкости с разрывом в антиферромагнетике Кагоме Гейзенберга". Наука. 350 (6261): 655–658. arXiv:1511.02174. Bibcode:2015Научный ... 350..655F. Дои:10.1126 / science.aab2120. PMID 26542565.
  38. ^ Хан, Тиан-Хенг и Норман, М.Р. и Вэнь, Джей-Джей и Родригес-Ривера, Хосе А. и Хелтон, Джоэл С. и Брохольм, Коллин и Ли, Янг С. (2016). «Коррелированные примеси и внутренняя физика спиновой жидкости в гербертсмитите материала кагоме». Физический обзор B. 94 (6): 060409. arXiv:1512.06807. Bibcode:2016PhRvB..94f0409H. Дои:10.1103 / PhysRevB.94.060409.CS1 maint: использует параметр авторов (связь)
  39. ^ а б c Amusia, M .; Попов, К .; Шагинян, В .; Стефанович В. (2014). Теория тяжелофермионных соединений - теория сильно коррелированных ферми-систем. Серия Спрингера в науках о твердом теле. 182. Springer. Дои:10.1007/978-3-319-10825-4. ISBN 978-3-319-10825-4.
  40. ^ а б Helton, J. S .; и другие. (1472). "Динамическое масштабирование восприимчивости Гербертсмитита решетчатого антиферромагнетика Спин-1/2 Кагоме". Письма с физическими проверками. 104 (14): 147201. arXiv:1002.1091. Bibcode:2010PhRvL.104n7201H. Дои:10.1103 / PhysRevLett.104.147201. PMID 20481955.
  41. ^ de Vries, M. A .; и другие. (2008). «Основное магнитное состояние экспериментального антиферромагнетика S = 1/2 kagomé». Письма с физическими проверками. 100 (15): 157205. arXiv:0705.0654. Bibcode:2008PhRvL.100o7205D. Дои:10.1103 / PhysRevLett.100.157205. PMID 18518149.
  42. ^ а б c Шагинян, В. Р .; Amusia, M. Ya .; Msezane, A. Z .; Попов, К. Г. (2010). «Масштабирование тяжелых фермионных металлов». Отчеты по физике. 492 (2–3): 31. arXiv:1006.2658. Bibcode:2010ФР ... 492 ... 31С. CiteSeerX 10.1.1.749.3376. Дои:10.1016 / j.physrep.2010.03.001.
  43. ^ Посо, Гильермо; де ла Преса, Патрисия; Прато, Рафаэль; Моралес, Ирен; Марин, Пилар; Франсаер, Ян; Домингес-Бенеттон, Сочитль (2020). «Наночастицы спинового перехода, полученные электрохимическим способом». Наномасштаб. 12: 5412–5421. Дои:10.1039 / C9NR09884D.
  44. ^ Gegenwart, P .; и другие. (2006). "Высокопольная фазовая диаграмма тяжелофермионного металла YbRh.2Si2". Новый журнал физики. 8 (9): 171. Bibcode:2006NJPh .... 8..171G. Дои:10.1088/1367-2630/8/9/171.
  45. ^ а б Шагинян, В. Р .; Msezane, A .; Попов, К. (2011). «Термодинамические свойства решетки Кагоме в ZnCu.3(ОЙ)6Cl2 Гербертсмитит ». Физический обзор B. 84 (6): 060401. arXiv:1103.2353. Bibcode:2011PhRvB..84f0401S. Дои:10.1103 / PhysRevB.84.060401.
  46. ^ Ин Ран, Майкл Хермеле, Патрик А. Ли, Сяо-Ган Вэнь, (2006), «Исследование прогнозируемых волновых функций модели Гейзенберга Spin-1/2 на решетке Кагоме», https://arxiv.org/abs/cond-mat/0611414
  47. ^ «Новое состояние вещества обнаружено в двумерном материале». Получено 5 апреля 2016.
  48. ^ Banerjee, A .; Bridges, C. A .; Yan, J.-Q .; Aczel, A. A .; Li, L .; Stone, M. B .; Granroth, G.E .; Lumsden, M.D .; Yiu, Y .; Knolle, J .; Bhattacharjee, S .; Коврижин, Д.Л .; Moessner, R .; Теннант, Д. А .; Mandrus, D.G .; Наглер, С. Э. (2016). «Поведение приближенной квантовой спиновой жидкости Китаева в сотовом магните». Материалы Природы. 15 (7): 733–740. arXiv:1504.08037. Bibcode:2016НатМа..15..733Б. Дои:10.1038 / nmat4604. PMID 27043779.
  49. ^ Бальц, Кристиан; Лейк, Белла; Рейтер, Йоханнес; Люткенс, Губертус; Шёнеманн, Рико; Херрманнсдёрфер, Томас; Сингх, Йогеш; Назмул Ислам, А. Т. М .; Уиллер, Элиза М .; Родригес-Ривера, Хосе А .; Гуиди, Татьяна; Симеони, Джованна Г .; Бейнс, Крис; Рилл, Ханджо (2016). «Физическая реализация квантовой спиновой жидкости на основе сложного механизма фрустрации». Природа Физика. 12 (10): 942–949. arXiv:1606.06463. Bibcode:2016НатФ..12..942Б. Дои:10.1038 / nphys3826.
  50. ^ а б Шагинян, В. Р .; и другие. (2012). «Идентификация сильно коррелированной спиновой жидкости в гербертсмитите». EPL. 97 (5): 56001. arXiv:1111.0179. Bibcode:2012EL ..... 9756001S. Дои:10.1209/0295-5075/97/56001.
  51. ^ Агилар, Марио (20 декабря 2012 г.). «Этот странный кристалл демонстрирует новое магнитное поведение, которое действует как волшебство». Gizmodo. Получено 24 декабря 2012.
  52. ^ Фендли, Пол. «Топологические квантовые вычисления по неабелевым энионам» (PDF). Университет Вирджинии. Получено 24 декабря 2012.
  53. ^ Чендлер, Дэвид (20 декабря 2012 г.). «Открыт новый вид магнетизма: эксперименты демонстрируют квантовую спиновую жидкость.'". Phys.org. Получено 24 декабря 2012.