WikiDer > Граф Робертсона
| Граф Робертсона | |
|---|---|
 Граф Робертсона гамильтонов. | |
| Названный в честь | Нил Робертсон |
| Вершины | 19 |
| Края | 38 |
| Радиус | 3 |
| Диаметр | 3 |
| Обхват | 5 |
| Автоморфизмы | 24 (D12) |
| Хроматическое число | 3 |
| Хроматический индекс | 5[1] |
| Толщина книги | 3 |
| Номер очереди | 2 |
| Характеристики | Клетка Гамильтониан |
| Таблица графиков и параметров | |
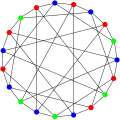
в математический поле теория графов, то Граф Робертсона или же (4,5) -клетка, это 4-обычный неориентированный граф с 19 вершинами и 38 ребрами, названными в честь Нил Робертсон.[2][3]
Граф Робертсона - единственный (4,5) -клеточный граф и был открыт Робертсоном в 1964 году.[4] Как клеточный граф, это самый маленький 4-регулярный граф с обхватом 5.
Она имеет хроматическое число 3, хроматический индекс 5, диаметр 3, радиус 3 и оба 4-вершинно-связанный и 4-реберный. Она имеет толщина книги 3 и номер очереди 2.[5]
Граф Робертсона также является Гамильтонов граф который содержит 5 376 различных направленных гамильтоновых циклов.
Алгебраические свойства
Граф Робертсона не является вершинно-транзитивный граф и его полная группа автоморфизмов изоморфна группе группа диэдра порядка 24 группа симметрий регулярного двенадцатигранник, включая как вращения, так и отражения.[6]
В характеристический многочлен графа Робертсона
Галерея
В хроматическое число графа Робертсона равно 3.
В хроматический индекс графа Робертсона равно 5.
Рекомендации
- ^ Вайсштейн, Эрик В. "График 2 класса". MathWorld.
- ^ Вайсштейн, Эрик В. "График Робертсона". MathWorld.
- ^ Бонди, Дж. А., Мёрти, США. Теория графов с приложениями. Нью-Йорк: Северная Голландия, стр. 237, 1976.
- ^ Робертсон, Н. «Наименьший граф 5 и валентности 4». Бык. Амер. Математика. Soc. 70, 824-825, 1964.
- ^ Джессика Вольц, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
- ^ Джеффри Эксу и Роберт Джейчай, Динамическое обследование клеток, Электр. J. Combin. 15, 2008.