WikiDer > Схема работы
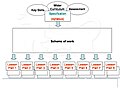
А схема работы[1][2] определяет структуру и содержание академического курса. Он разбивает учебную программу, рассчитанную на несколько лет, на готовые единицы работы, продолжительность каждой из которых намного короче (например, две или три недели). Затем каждая единица работы анализируется на отдельные темы, которые можно преподать, даже меньшей продолжительности (например, два часа или меньше).
Более эффективные схемы работы четко определяют, как ресурсы (например, книги, оборудование, время) и классные занятия (например, беседа с учителем, групповая работа, практические занятия, обсуждения) и оценка стратегии (например, тесты, викторины, вопросы и ответы, домашнее задание) будет использоваться для преподавания каждой темы и оценки успеваемости студентов в изучении материала, связанного с каждой темой, блоком и схемой работы в целом. По мере того, как студенты продвигаются по схеме работы, ожидается, что их восприятие взаимосвязей между темами и разделами будет улучшаться.
Схемы работы могут включать время и даты (крайние сроки) выполнения различных элементов учебной программы. С философской точки зрения это связано с убеждением, что все учащиеся должны быть знакомы со всеми элементами учебной программы, чтобы те, кто способен «не отставать» («лучшие» / элитные), не упускали ни одного содержания и могли достичь высшие оценки. Это можно охарактеризовать как «традиционалистский» взгляд.
Существует противоречивое философское мнение о том, что следует избегать дедлайнов и что каждый класс должен продвигаться в своем собственном темпе: так, чтобы ни один ученик не был «оставлен позади». Пока оставшиеся ученики «догоняют», те ученики, которые понимают быстро, должны быть помещены в «схему ожидания», полную головоломок и вопросов, которые заставят их связать недавнее обучение с более длительным обучением (их также можно поощрить потратить небольшой количество времени на улучшение их понимания, поддерживая преподавательский состав в выявлении основных ошибок / вопросов сокурсников, которые не так быстро уловили недавние идеи). Этот взгляд можно охарактеризовать как подход «мастерства». В преподавании математики в Англии его активно поддерживает Государственный национальный центр передового опыта в области преподавания математики.[3] основан на исследовании, основанном на выдающихся мировых достижениях школ Сингапура и Шанхая.
Учебный план
В схема работы обычно интерпретация спецификации или учебный план и может использоваться в качестве руководства на протяжении всего курса для отслеживания прогресса по первоначальному плану. Схемы работы могут быть предоставлены студентам, чтобы они имели представление о своем курсе.
Конечным источником спецификации или программы является учебная программа. Учебные планы обычно определяются правительством и, следовательно, законом и / или постановлением. Соответственно, у каждой страны свои собственные (хотя некоторые страны предпочитают принимать учебные программы, определенные другими странами).
При создании схема работы, очень важно внимательно изучить юридически обязательную учебную программу страны, в которой схема работы должен быть доставлен. Обычно они подробно определяются по темам. Понимание тонкостей и нюансов их представления имеет жизненно важное значение при определении наиболее полезных схемы работы.
Англия
Для обслуживаемых школ[4] и экзаменационные комиссии[5] в Англии национальная учебная программа устанавливается Министерством образования.[6] так что все дети, растущие в Англии, имеют в целом одинаковое образование.
Учебная программа начального образования (от 4/5 до 11 лет) и среднего образования (от 11 до 18 лет) в Англии разделена на пять основных этапов. Ключевые этапы 1 и 2 проводятся в начальных школах. Ключевые ступени 3, 4 и 5 преподаются в средних школах.
Англия - математика[7]
Английские начальные школы: основные этапы 1 и 2 [от 5 до 11 лет]
Ожидания по доставке Национальной учебной программы по математике в Англии на ключевых этапах 1 и 2 четко определены с четкими целями, привязанными ко времени. Департамент образования предоставил первоначальную годовую схему работы.[8] (или набор ожиданий) для каждого учебного года с 1 класса (возраст 5/6 лет) до 6 класса включительно (возраст 10/11 лет). Здесь не указан порядок преподавания каждой темы в течение года; но дает рекомендации и излагает ожидания относительно того, чему нужно учить и чему научиться к концу каждого года начальной школы.
Английские средние школы: основные этапы 3 и 4 [в возрасте от 11 до 16 лет]
Национальная учебная программа по математике в Англии также четко определена на ключевых этапах 3 и 4.[9]. Тем не менее, отдел математики каждой английской школы имеет большую свободу решать, когда и как доставлять материалы. В отличие от национальной учебной программы для начальных школ Англии, здесь нет ежегодных ожиданий. Вместо этого руководство устанавливается со ссылкой на то, что следует преподавать и выучить к концу ключевого этапа 3 [конец 9 года (возраст 13/14 лет)] и к концу ключевого этапа 4 [конец 11 года ( возраст 15/16)].
Примечательно, что учебная программа для ключевого этапа 4 предназначена Министерством образования для изучения всего обучения с ключевых этапов 1–4. В частности, темы, перечисленные в ключевом этапе 3, явным образом составляют часть учебной программы для ключевого этапа 4.[10] (таким образом, чтобы основы более раннего обучения укреплялись по мере их развития). Соответственно, учащимся, которые в прошлом боролись с более сложными для понимания элементами, предоставляется возможность освоить контент ключевого этапа 3, в то время как другие параллельно развивают более высокий уровень.
Английские средние школы: GCSE [обычно возраст 15/16 +]
В Англии учащиеся обязаны сдать GCSE по математике в год своего шестнадцатилетия.
Примечательно, что содержание предмета согласовано между Департаментом образования и Управлением по регулированию квалификаций и экзаменов (Ofqual) [регулирующим органом экзаменационной комиссии для GCSE, AS-Levels и A-Levels][11] выделяется несколько иначе, чем предметное содержание национальной учебной программы для ключевого этапа 4[12].
Последний имеет два уровня ожидания (простой текст и {полужирный и фигурные скобки}); в первом есть три (обычный текст, подчеркнутый текст и жирный текст). Тонкое различие позволило более проницательным ученикам, родителям и преподавателям определить (или предположить), каким образом контент распределяется (или должен распределяться) между двумя разными наборами экзаменов по математике GCSE (Foundation и Higher): эти два набора перекрываются (предполагая подчеркнутый темы существуют на пересечении двух наборов тем).
Также примечательно, что учебная программа для GCSE предназначена Министерством образования для изучения всего обучения от ключевых этапов 1 до 4. В частности, темы, перечисленные в ключевом этапе 3, явным образом составляют часть учебной программы для ключевого этапа 4[10] и GCSE (таким образом, что основы более раннего обучения укрепляются, опираясь на них). Соответственно, учащимся, которые в прошлом боролись с более сложными для понимания элементами, предоставляется возможность освоить контент ключевого этапа 3, в то время как другие параллельно развивают более высокий уровень.
Английские средние школы: AS и A-Levels [обычно возраст 17+]
AS и A-Levels по математике не являются обязательными.
Соответственно, в Англии нет национальной учебной программы по математике AS и A-Level. Тем не менее, существует согласованное предметное содержание, требуемое Министерством образования для AS и Уровень спецификации по математике[13].
Элементы
Ключевые части «схемы работы» могут включать:
| Содержание 1 |
| Цели или результаты |
| Способы доставки (деятельность студентов и преподавателей) |
| Стратегии оценки |
| Ресурсы |
| Прочие примечания |
Пример простого схема работы
Смотрите также Планы урока.
Рекомендации
Схемы работы [1]
- ^ Петти, Джеффри. (2009). Преподавание сегодня: практическое руководство (4-е изд.). Челтнем: Нельсон Торнс. С. 469–473. ISBN 978-1-4085-0415-4. OCLC 295002509.
- ^ Учимся преподавать в средней школе: товарищ по школьному опыту. Капел, Сьюзан Энн, 1953-, Лиск, Мэрилин, 1950-, Тернер, Тони, 1935- (4-е изд.). Лондон: Рутледж. 2005. С. 78–90. ISBN 0-415-36392-6. OCLC 58468269.CS1 maint: другие (связь)
- ^ «Как мы можем удовлетворить потребности всех учеников без дифференциации содержания урока? Как мы можем фиксировать прогресс без уровней? - NCETM». www.ncetm.org.uk. Получено 2019-12-22.
- ^ "Национальная программа". GOV.UK. Получено 2019-12-22.
- ^ «Аккредитация GCSE, AS и A уровней для обучения с 2017 года». GOV.UK. Получено 2019-12-22.
- ^ "Национальная программа". GOV.UK. Получено 2019-12-22.
- ^ «Национальная учебная программа в Англии: программы изучения математики». GOV.UK. Получено 2019-12-22.
- ^ «Национальная учебная программа в Англии: программы изучения математики». GOV.UK. Получено 2019-12-22.
- ^ «Национальная учебная программа в Англии: программы изучения математики». GOV.UK. Получено 2019-12-22.
- ^ а б «Национальная учебная программа в Англии: программы изучения математики». GOV.UK. Получено 2019-12-22.
- ^ "GCSE математика". GOV.UK. Получено 2019-12-22.
- ^ «Национальная учебная программа в Англии: программы изучения математики». GOV.UK. Получено 2019-12-22.
- ^ "Математика уровня AS и A". GOV.UK. Получено 2019-12-22.