WikiDer > Сектрикс Маклорена

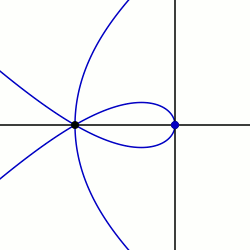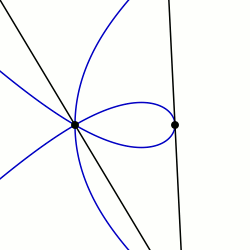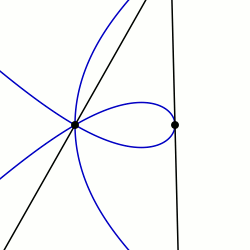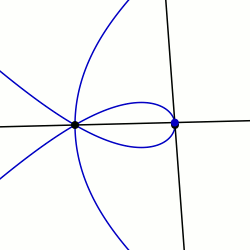
Сектрикс Маклорена: пример с q0 = PI / 2 и K = 3

В геометрия, а сектриса Маклорена определяется как кривая, проходящая через точку пересечения двух линий, каждая из которых вращается с постоянной скоростью вокруг разных точек, называемых полюса. Эквивалентно сектрису Маклорена можно определить как кривую, уравнение которой в двуугольные координаты линейно. Название происходит от трисектрикс Маклорена (назван в честь Колин Маклорен), который является выдающимся членом семьи, и их сектрикс свойство, что означает, что их можно использовать для разделения угла на заданное количество равных частей. Есть особые случаи, также известные как паукообразный или же аранейданс из-за их паук-подобная форма, и Кривые плато после Плато Джозеф кто их изучал.

Уравнения в полярных координатах

Нам даны две линии, вращающиеся вокруг двух полюсов ${displaystyle P}$ и ${displaystyle P_ {1}}$. Путем перевода и вращения мы можем считать ${displaystyle P = (0,0)}$ и ${displaystyle P_ {1} = (а, 0)}$. Вовремя ${displaystyle t}$, линия, вращающаяся вокруг ${displaystyle P}$ имеет угол ${displaystyle heta = kappa t + alpha}$ и линия, вращающаяся вокруг ${displaystyle P_ {1}}$ имеет угол ${displaystyle heta _ {1} = kappa _ {1} t + alpha _ {1}}$, куда ${displaystyle kappa}$, ${displaystyle alpha}$, ${displaystyle kappa _ {1}}$ и ${displaystyle alpha _ {1}}$ являются константами. Устранять ${displaystyle t}$ получить ${displaystyle heta _ {1} = q heta + heta _ {0}}$ куда ${displaystyle q = kappa _ {1} / kappa}$ и ${displaystyle heta _ {0} = alpha _ {1} -qalpha}$. Мы предполагаем ${displaystyle q}$ рационально, иначе кривая не является алгебраической и плотна на плоскости. Позволять ${displaystyle Q}$ - точка пересечения двух прямых, и пусть ${displaystyle psi}$ быть углом в ${displaystyle Q}$, так ${displaystyle psi = heta _ {1} - heta}$. Если ${displaystyle r}$ это расстояние от ${displaystyle P}$ к ${displaystyle Q}$ затем, по закон синуса,

${displaystyle {r over sin heta _ {1}} = {a over sin psi}!}$

так

${displaystyle r = a {frac {sin heta _ {1}} {sin psi}} = a {frac {sin [q heta + heta _ {0}]} {sin [(q-1) heta + heta _ { 0}]}}!}$

- уравнение в полярных координатах.

Дело ${displaystyle heta _ {0} = 0}$ и ${displaystyle q = n}$ куда ${displaystyle n}$ целое число больше 2 дает кривые паукообразных или аранейдановых

${displaystyle r = a {frac {sin n heta} {sin (n-1) heta}}!}$

Дело ${displaystyle heta _ {0} = 0}$ и ${displaystyle q = -n}$ куда ${displaystyle n}$ целое число больше 1 дает альтернативные формы кривых паукообразных или аранейдановых

${displaystyle r = a {frac {sin n heta} {sin (n + 1) heta}}!}$

Вывод, аналогичный приведенному выше, дает

${displaystyle r_ {1} = (- a) {frac {sin [(1 / q) heta _ {1} - heta _ {0} / q]} {sin [(1 / q-1) heta _ {1 } - heta _ {0} / q]}}!}$

как полярное уравнение (в ${displaystyle r_ {1}}$ и ${displaystyle heta _ {1}}$), если начало координат сдвинуто вправо на ${displaystyle a}$. Обратите внимание, что это более раннее уравнение с изменением параметров; этого следовало ожидать из того факта, что два полюса взаимозаменяемы при построении кривой.

Уравнения в комплексной плоскости, прямоугольные координаты и ортогональные траектории

Позволять ${displaystyle q = m / n}$ куда ${displaystyle m}$ и ${displaystyle n}$ - целые числа, а дробь - в младших членах В обозначениях предыдущего раздела имеем ${displaystyle heta _ {1} = q heta + heta _ {0}}$ или же ${displaystyle n heta _ {1} = m heta + n heta _ {0}}$.Если ${displaystyle z = x + iy}$ тогда ${displaystyle heta = arg (z), heta _ {1} = arg (z-a)}$, поэтому уравнение принимает вид${displaystyle n arg (z-a) = m arg (z) + n heta _ {0}}$ или же ${displaystyle m arg (z) -n arg (z-a) = arg (z ^ {m} (z-a) ^ {- n}) = const}$. Это также можно написать

${displaystyle {frac {имя оператора {Re} (z ^ {m} (za) ^ {- n})} {имя оператора {Im} (z ^ {m} (za) ^ {- n})}} = const. }$

из которого относительно просто вывести декартово уравнение с заданными m и n. Функция ${displaystyle w = z ^ {m} (z-a) ^ {- n}}$ аналитична, поэтому ортогональные траектории семейства ${displaystyle arg (w) = const.}$ кривые ${displaystyle | w | = const}$, или же${displaystyle {frac {| z | ^ {m}} {| z-a | ^ {n}}} = const.}$

Параметрические уравнения

Позволять ${displaystyle q = m / n}$ куда ${displaystyle m}$ и ${displaystyle n}$ целые числа, и пусть ${displaystyle heta = np}$ куда ${displaystyle p}$ является параметром. Затем преобразовав полярное уравнение выше к параметрические уравнения производит

${displaystyle x = a {frac {sin [mp + heta _ {0}] cos np} {sin [(mn) p + heta _ {0}]}}, y = a {frac {sin [mp + heta _ {0}] ] sin np} {sin [(mn) p + heta _ {0}]}}!}$.

Применение правила сложения углов для синуса дает

${displaystyle x = a {frac {sin [mp + heta _ {0}] cos np} {sin [(mn) p + heta _ {0}]}} = a + a {frac {cos [mp + heta _ {0}] ] sin np} {sin [(mn) p + heta _ {0}]}} = {a over 2} + {a over 2} {frac {sin [(m + n) p + heta _ {0}]} { sin [(mn) p + heta _ {0}]}}!}$.

Таким образом, если начало координат сдвинуто вправо на a / 2, то параметрические уравнения будут

${displaystyle x = {a over 2} cdot {frac {sin [(m + n) p + heta _ {0}]} {sin [(mn) p + heta _ {0}]}}, y = a {frac { sin [mp + heta _ {0}] sin np} {sin [(mn) p + heta _ {0}]}}!}$.

Это уравнения для кривых Плато, когда ${displaystyle heta _ {0} = 0}$, или же

${displaystyle x = {a over 2} {frac {sin (m + n) p} {sin (m-n) p}}, y = a {frac {sin mpsin np} {sin (m-n) p}}!}$.

Инверсивные тройни

В обратный относительно окружности радиуса a с центром в начале координат

${displaystyle r = a {frac {sin [q heta + heta _ {0}]} {sin [(q-1) heta + heta _ {0}]}}}$

является

${displaystyle r = a {frac {sin [(q-1) heta + heta _ {0}]} {sin [q heta + heta _ {0}]}} = a {frac {sin [(1-q) хета - хета _ {0}]} {грех [((1-q) -1) хета - хета _ {0}]}}}$.

Это еще одна кривая в семье. Инверсия по отношению к другому полюсу дает еще одну кривую в том же семействе, а две инверсии, в свою очередь, противоположны друг другу. Следовательно, каждая кривая в семействе является членом тройки, каждая из которых принадлежит семейству и является обратной по отношению к двум другим. Значения q в этом семействе равны

${displaystyle q, {frac {1} {q}}, 1-q, {frac {1} {1-q}}, {frac {q-1} {q}}, {frac {q} {q- 1}}}$.

Свойства Sectrix

Позволять ${displaystyle q = m / n}$ куда ${displaystyle m}$ и ${displaystyle n}$ являются целыми числами в младших членах и предполагают ${displaystyle heta _ {0}}$ является строится с компасом и линейкой. (Значение ${displaystyle heta _ {0}}$ на практике обычно равно 0, поэтому обычно это не проблема.) Пусть ${displaystyle varphi}$ - заданный угол, и предположим, что секта Маклорена нарисована полюсами ${displaystyle P}$ и ${displaystyle P_ {1}}$ согласно приведенной выше конструкции. Построить луч из ${displaystyle P_ {1}}$ под углом ${displaystyle varphi + heta _ {0}}$ и разреши ${displaystyle Q}$ быть точкой пересечения луча и сектрисы и нарисуйте ${displaystyle PQ}$. Если ${displaystyle heta}$ угол этой линии, тогда

${displaystyle varphi + heta _ {0} = heta _ {1} = q heta + heta _ {0}}$

так ${displaystyle heta = {frac {nvarphi} {m}}}$.Путем многократного вычитания ${displaystyle heta}$ и ${displaystyle varphi}$ друг от друга, как в Евклидов алгоритм, угол ${displaystyle varphi / m}$ могут быть построены. Таким образом, кривая представляет собой м-сектриса, означающая, что с помощью кривой произвольный угол можно разделить на любое целое число. Это обобщение концепции трисектриса и их примеры можно найти ниже.

Теперь нарисуйте луч с углом ${displaystyle varphi}$ из ${displaystyle P}$ и ${displaystyle Q '}$ - точка пересечения этого луча с кривой. Угол ${displaystyle P'Q '}$ является

${displaystyle heta _ {1} = q heta + heta _ {0} = qvarphi + heta _ {0}}$

и вычитая ${displaystyle heta _ {0}}$ дает угол

${displaystyle qvarphi = {frac {mvarphi} {n}}}$.

Повторное применение алгоритма Евклида дает угол ${displaystyle varphi / n}$ показывая, что кривая также является п-сектрикс.

Наконец, нарисуйте луч из ${displaystyle P}$ с углом ${displaystyle pi / 2-varphi - heta _ {0}}$ и луч от ${displaystyle P '}$ с углом ${displaystyle pi / 2 + varphi + heta _ {0}}$, и разреши ${displaystyle C}$ быть точкой пересечения. Эта точка находится на серединном перпендикуляре к ${displaystyle PP '}$ так что есть круг с центром ${displaystyle C}$ содержащий ${displaystyle P}$ и ${displaystyle P '}$. ${displaystyle angle PCP '= 2 (varphi + heta _ {0})}$ поэтому любая точка на окружности образует угол ${displaystyle varphi + heta _ {0}}$ между ${displaystyle P}$ и ${displaystyle P '}$. (Это, по сути, один из Аполлонические круги из п и П'.) Позволять ${displaystyle Q ''}$ точка пересечения этой окружности и кривой. потом ${displaystyle varphi + heta _ {0} = angle PQ''P '= psi = heta _ {1} - heta = (q-1) heta + heta _ {0}}$так

${displaystyle varphi = {frac {(m-n) heta} {n}}, heta = {frac {n heta} {m-n}}}$.

Применение алгоритма Евклида в третий раз дает угол ${displaystyle varphi / (м-п)}$, показывая, что кривая представляет собой (м−п) -сектрисы.

Конкретные случаи

q = 0

Это кривая

${displaystyle r = a {frac {sin heta _ {0}} {sin (- heta + heta _ {0})}}}$

который проходит через ${displaystyle (a, 0)}$

q = 1

Это круг, содержащий начало и ${displaystyle (a, 0)}$. Он имеет полярное уравнение

${displaystyle r = a {frac {sin (heta + heta _ {0})} {sin heta _ {0}}}}$.

Это обратное по отношению к происхождению q = 0 случай. Ортогональные траектории семейства окружностей - это семейство ${displaystyle {frac {| z-a |} {| z |}} = const.}$ Они образуют Аполлонические круги с шестами ${displaystyle (0,0)}$ и ${displaystyle (a, 0)}$.

q = -1

Эти кривые имеют полярное уравнение

${displaystyle r = a {frac {sin (- heta + heta _ {0})} {sin (-2 heta + heta _ {0})}}}$,

сложное уравнение ${displaystyle arg (z (z-a)) = const.}$ В прямоугольных координатах это становится${displaystyle x ^ {2} -y ^ {2} -x = c (2xy-y)}$ которая является конической. Из полярного уравнения видно, что кривые имеют асимптоты при ${displaystyle heta = heta _ {0} / 2}$ и ${displaystyle heta _ {0} / 2 + pi / 2}$ которые находятся под прямым углом. Таким образом, коники представляют собой прямоугольные гиперболы. Центр гиперболы всегда ${displaystyle (a / 2,0)}$. Ортогональные траектории этого семейства задаются формулами ${displaystyle | z || z-a | = c}$ которая является семьей Кассини овалы с фокусами ${displaystyle (0,0)}$ и ${displaystyle (a, 0)}$.

Трисектрикс Маклорена

В случае, когда ${displaystyle q = 3}$ (или же ${displaystyle q = 1/3}$ переключением полюсов) и ${displaystyle heta _ {0} = 0}$, уравнение

${displaystyle r = a {frac {sin 3 heta} {sin 2 heta}} = {a over 2} {frac {4cos ^ {2} heta -1} {cos heta}} = {a over 2} (4cos heta -sec heta)}$.

Это Трисектрикс Маклорена что является частным случаем, обобщением которого является сектриса Маклорена. Приведенная выше конструкция дает метод, позволяющий использовать эту кривую как трисектрису.

Лимасон трисектрикс

В случае, когда ${displaystyle q = 3/2}$ (или же ${displaystyle q = 2/3}$ переключением полюсов) и ${displaystyle heta _ {0} = 0}$, уравнение

${displaystyle r = a {frac {sin {frac {3} {2}} heta} {sin {frac {1} {2}} heta}} = a (3cos ^ {2} {frac {1} {2}) } heta -sin ^ {2} {frac {1} {2}} heta) = a (1 + 2cos heta)}$.

Это Лимасон трисектрикс. Уравнение с началом координат принимаем за другой полюс:

${displaystyle r = -a {frac {sin {frac {2} {3}} heta} {sin - {frac {1} {3}} heta}} = 2acos {frac {1} {3}} heta}$.

3 в числителе q и приведенная выше конструкция дает метод, позволяющий использовать кривую как трисектрису.

Рекомендации

• "Sectrice de Maclaurin" в Encyclopédie des Formes Mathématiques Remarquables (На французском)
• Вайсштейн, Эрик В. "Арахнида". MathWorld.
• Вайсштейн, Эрик В. «Кривые плато». MathWorld.