WikiDer > Метод стрельбы - Википедия
В числовой анализ, то метод стрельбы это метод решения краевая задача сводя его к системе проблема начального значения. Грубо говоря, мы «стреляем» по траекториям в разные стороны, пока не найдем траекторию с желаемым граничным значением. Следующее изложение может быть пояснено этим. иллюстрация способа стрельбы.
Для краевой задачи второго порядка обыкновенное дифференциальное уравнение, метод изложен следующим образом.
- краевая задача. у(т; а) обозначают решение начальной задачи
Определите функцию F(а) как разница между у(т1; а) и заданное граничное значение у1.
Если F имеет корень а тогда решение у(т; а) соответствующей начальной задачи также является решением краевой задачи. И наоборот, если краевая задача имеет решение у(т), тогда у(т) также является единственным решением у(т; а) начальной задачи где а = у'(т0), таким образом а это корень F.
Здесь можно использовать обычные методы поиска корней, такие как метод деления пополам или же Метод Ньютона.
Происхождение термина
Термин «метод стрельбы» берет свое начало в артиллерии. При стрельбе из пушки по цели первый выстрел производится в общем направлении цели. Если ядро попадает слишком далеко вправо, орудие направляется немного влево для второго выстрела, и наоборот. Таким образом, ядра будут попадать все ближе к цели.
Линейный метод стрельбы
Краевая задача линейна, если ж имеет форму
В этом случае решение краевой задачи обычно дает:
куда является решением задачи начального значения:
и является решением задачи начального значения:
Видеть доказательство для точного условия, при котором выполняется этот результат.
Пример
А краевая задача дается Стоером и Булиршем следующим образом[1] (Раздел 7.3.1).
В проблема начального значения
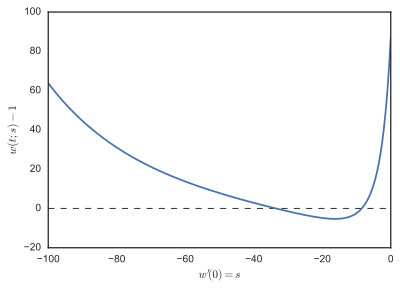
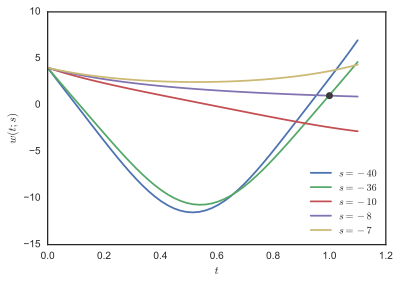
было решено для s = −1, −2, −3, ..., −100 и F(s) = ш(1;s) - 1 нанесено на первый рисунок. F, мы видим, что есть корни вблизи −8 и −36. Некоторые траектории ш(т;s) показаны на втором рисунке.
Стоер и Булирш[1] утверждают, что есть два решения, которые могут быть найдены алгебраическими методами, они соответствуют начальным условиям ш′ (0) = −8 и ш′ (0) = −35,9 (приблизительно).
Смотрите также
Примечания
Рекомендации
- Нажмите, WH; Теукольский С.А.; Феттерлинг, штат Вашингтон; Фланнери, ВР (2007). «Раздел 18.1. Метод стрельбы». Числовые рецепты: искусство научных вычислений (3-е изд.). Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-88068-8.
внешняя ссылка
- Краткое описание ODEPACK (в Netlib; содержит LSODE)
- Съемочный метод решения краевых задач - Notes, PPT, Maple, Mathcad, Matlab, Mathematica в Институт целостных численных методов [1]