WikiDer > Коник Штейнера - Википедия

Steiner conic - Wikipedia

1. Определение генерации Штейнера конического сечения.

В Конус Штейнера или точнее Поколение конуса Штейнера, названный в честь швейцарского математика Якоб Штайнер, является альтернативным методом определения невырожденного проективное коническое сечение в проективная плоскость через поле.

Обычное определение коники использует квадратичную форму (см. Квадрика (проективная геометрия)). Другое альтернативное определение коники использует гиперболическая полярность. Это связано с К. Г. К. фон Штаудт и иногда называли фон Штаудт конический. Недостатком определения фон Штаудта является то, что оно работает только тогда, когда базовое поле имеет нечетное значение. характеристика (т.е. ${ displaystyle Char neq 2}$ ).

Определение коники Штейнера

Учитывая два карандаши ${ Displaystyle B (U), B (V)}$ линий в двух точках ${ displaystyle U, V}$ (все строки, содержащие ${ displaystyle U}$ и ${ displaystyle V}$ соотв.) и проективное, но не перспективное отображение ${ displaystyle pi}$ из ${ Displaystyle B (U)}$ на ${ Displaystyle B (V)}$ . Тогда точки пересечения соответствующих прямых образуют невырожденное проективное коническое сечение^[1]^[2]^[3] ^[4] (Рисунок 1)

2. Отображение перспективы между линиями

А перспектива отображение ${ displaystyle pi}$ карандаша ${ Displaystyle B (U)}$ на карандаш ${ Displaystyle B (V)}$ это биекция (Соответствие 1-1) такое, что соответствующие прямые пересекаются на фиксированной прямой ${ displaystyle a}$ , который называется ось перспективы ${ displaystyle pi}$ (фигура 2).

А проективный отображение - это конечный продукт перспективных отображений.

Простой пример: Если переместиться в первую точку диаграммы ${ displaystyle U}$ и его карандаш линий на ${ displaystyle V}$ и вращает сдвинутый карандаш вокруг ${ displaystyle V}$ на фиксированный угол ${ displaystyle varphi}$ тогда сдвиг (перенос) и вращение порождают проективное отображение ${ displaystyle pi}$ карандаша в точке ${ displaystyle U}$ на карандаш в ${ displaystyle V}$ . От теорема о вписанном угле получается: точки пересечения соответствующих линий образуют круг.

Примеры часто используемых полей - реальные числа ${ Displaystyle mathbb {R}}$ , рациональные числа ${ displaystyle mathbb {Q}}$ или комплексные числа ${ displaystyle mathbb {C}}$ . Конструкция также работает над конечными полями, обеспечивая примеры в конечных полях. проективные плоскости.

Замечание:Основная теорема для проективных плоскостей утверждает,^[5] что проективное отображение на проективной плоскости над полем (паппийский самолет) однозначно определяется заданием изображений трех линий. Это означает, что для конического сечения Штейнера кроме двух точек ${ displaystyle U, V}$ необходимо указать только изображения трех строк. Эти 5 элементов (2 точки, 3 линии) однозначно определяют коническое сечение.

Замечание:Обозначение «перспектива» связано с двойным утверждением: проекция точек на линию ${ displaystyle a}$ из центра ${ displaystyle Z}$ на линию ${ displaystyle b}$ называется перспективность (видеть ниже).^[5]

3. Пример генерации Штейнера: генерация точки

Пример

Для следующего примера изображения линий ${ displaystyle a, u, w}$ (см. рисунок) приведены: ${ Displaystyle пи (а) = Ь, пи (и) = ш, пи (ш) = v}$ . Проективное отображение ${ displaystyle pi}$ является результатом следующих отображений перспективы ${ displaystyle pi _ {b}, pi _ {a}}$ : 1) ${ displaystyle pi _ {b}}$ перспективное отображение карандаша в точке ${ displaystyle U}$ на карандаш в точке ${ displaystyle O}$ с осью ${ displaystyle b}$ . 2) ${ displaystyle pi _ {a}}$ перспективное отображение карандаша в точке ${ displaystyle O}$ на карандаш в точке ${ displaystyle V}$ с осью ${ displaystyle a}$ .Сначала следует проверить, что ${ displaystyle pi = pi _ {a} pi _ {b}}$ имеет свойства: ${ Displaystyle пи (а) = Ь, пи (и) = ш, пи (ш) = v}$ . Следовательно, для любой строки ${ displaystyle g}$ изображение ${ displaystyle pi (g) = pi _ {a} pi _ {b} (g)}$ могут быть построены и, следовательно, образы произвольного набора точек. Линии ${ displaystyle u}$ и ${ displaystyle v}$ содержат только конические точки ${ displaystyle U}$ и ${ displaystyle V}$ соотв .. Следовательно ${ displaystyle u}$ и ${ displaystyle v}$ являются касательными к сформированному коническому сечению.

А доказательство то, что этот метод генерирует коническое сечение, следует из перехода к аффинному ограничению с прямой ${ displaystyle w}$ как линия на бесконечности, точка ${ displaystyle O}$ как начало системы координат с точками ${ displaystyle U, V}$ в качестве указывает на бесконечность из Икс- и уось соотв. и указать ${ Displaystyle E = (1,1)}$ . Аффинная часть сгенерированной кривой оказывается гипербола ${ Displaystyle у = 1 / х}$ .^[2]

Замечание:

Генерация конического сечения Штейнера обеспечивает простые методы построения эллипсы, параболы и гиперболы которые обычно называют методы параллелограмма.
Фигура, которая появляется при построении точки (рисунок 3), является 4-точечным вырождением Теорема Паскаля.^[6]

Штейнеровская генерация двойной коники

двойной эллипс

Штейнеровская генерация двойной коники

определение перспективного отображения

Определения и двойное поколение

Дуализация (см. двойственность (проективная геометрия)) проективная плоскость означает замену точки с линии и операции пересечение и соединение. Двойственная структура проективной плоскости также является проективной плоскостью. Двойственная плоскость папповой плоскости является папской и также может быть согласована с помощью однородных координат. Невырожденный двойная коническая сечение аналогично определяется квадратичной формой.

Двойственная коника может быть получена двойственным методом Штейнера:

Учитывая наборы точек двух линий ${ displaystyle u, v}$ и проективное, но не перспективное отображение ${ displaystyle pi}$ из ${ displaystyle u}$ на ${ displaystyle v}$ . Тогда прямые, соединяющие соответствующие точки, образуют двойственное невырожденное проективное коническое сечение.

А перспективное отображение ${ displaystyle pi}$ точки набора линии ${ displaystyle u}$ на точечный набор линии ${ displaystyle v}$ это биекция (Соответствие 1-1) такое, что соединительные линии соответствующих точек пересекаются в фиксированной точке ${ displaystyle Z}$ , который называется центр перспективы ${ displaystyle pi}$ (см. рисунок).

А проективный отображение - это конечная последовательность перспективных отображений.

Обычно, имея дело с двойными и общими коническими сечениями, общее коническое сечение обычно называют точечный конический и двойственная коника a линия коническая.

В случае, если базовое поле имеет ${ displaystyle Char = 2}$ все касательные точки коники пересекаются в точке, называемой морской узел (или же ядро) коники. Таким образом, двойственная невырожденная точечная коника - это подмножество точек двойственной прямой, а не овальная кривая (в двойственной плоскости). Итак, только в том случае, если ${ displaystyle Char neq 2}$ является двойственной невырожденной точечной конике к невырожденной прямой конике.

Примеры

Двойная коника Штейнера, определяемая двумя перспективами

{ displaystyle pi _ {A}, pi _ {B}}

пример генерации Штейнера двойственной коники

(1) Проективность, заданная двумя перспективами:
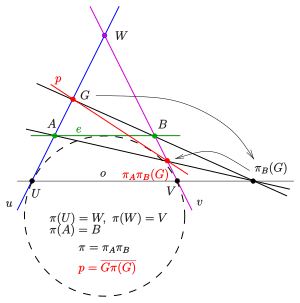
Две строки ${ displaystyle u, v}$ с точкой пересечения ${ displaystyle W}$ даны и проективность ${ displaystyle pi}$ из ${ displaystyle u}$ на ${ displaystyle v}$ с двух точек зрения ${ displaystyle pi _ {A}, pi _ {B}}$ с центрами ${ displaystyle A, B}$ . ${ displaystyle pi _ {A}}$ линия карт ${ displaystyle u}$ на третью линию ${ displaystyle o}$ , ${ displaystyle pi _ {B}}$ линия карт ${ displaystyle o}$ на линию ${ displaystyle v}$ (см. диаграмму). Точка ${ displaystyle W}$ не должен лежать на линиях ${ displaystyle { overline {AB}}, о}$ . Проективность ${ displaystyle pi}$ представляет собой сочетание двух перспектив: ${ displaystyle pi = pi _ {B} pi _ {A}}$ . Следовательно, точка ${ displaystyle X}$ отображается на ${ displaystyle pi (X) = pi _ {B} pi _ {A} (X)}$ и линия ${ Displaystyle х = { overline {X pi (X)}}}$ является элементом двойственной коники, определяемой ${ displaystyle pi}$ .
(Если ${ displaystyle W}$ будет фиксированной точкой, ${ displaystyle pi}$ было бы перспективно ^[7].)

(2) Даны три точки и их изображения:
Следующий пример является двойственным, приведенным выше для коники Штейнера.
Изображения точек ${ displaystyle A, U, W}$ даны: ${ Displaystyle пи (А) = В, , пи (U) = W, , пи (W) = V}$ . Проективное отображение ${ displaystyle pi}$ может быть представлена продуктом следующих перспектив ${ displaystyle pi _ {B}, pi _ {A}}$ :

1)

{ displaystyle pi _ {B}}

- перспективность точечного набора линии

{ displaystyle u}

на точечный набор линии

{ displaystyle o}

с центром

{ displaystyle B}

.

2)

{ displaystyle pi _ {A}}

- перспективность точечного набора линии

{ displaystyle o}

на точечный набор линии

{ displaystyle v}

с центром

{ displaystyle A}

.

Несложно проверить, что проективное отображение ${ displaystyle pi = pi _ {A} pi _ {B}}$ выполняет ${ Displaystyle пи (А) = В, , пи (U) = W, , пи (W) = V}$ . Следовательно, для любой произвольной точки ${ displaystyle G}$ изображение ${ Displaystyle pi (G) = pi _ {A} pi _ {B} (G)}$ могут быть построены и линии ${ Displaystyle { overline {G pi (G)}}}$ является элементом невырожденного двойственного конического сечения. Потому что точки ${ displaystyle U}$ и ${ displaystyle V}$ содержатся в строках ${ displaystyle u}$ , ${ displaystyle v}$ соответственно, точки ${ displaystyle U}$ и ${ displaystyle V}$ - точки коники, а прямые ${ displaystyle u, v}$ касательные в ${ displaystyle U, V}$ .

Примечания

^ Кокстер 1993, п. 80
^ ^а ^б Hartmann, п. 38
^ Мерсерв 1983, п. 65
^ Vorlesungen über Synthetische Geometrie Якоба Штайнера, Б. Г. Тойбнер, Лейпциг 1867 г. (из Google Книги: (Немецкий) Часть II следует за Частью I) Часть II, стр. 96
^ ^а ^б Hartmann, п. 19
^ Hartmann, п. 32
^ Х. Ленц: Vorlesungen über projektive Geometrie, Б.И., Мангейм, 1965, с. 49.

Navigation

Navigation

Themenportale

WikiDer > Коник Штейнера - Википедия

Содержание

Определение коники Штейнера

Пример

Штейнеровская генерация двойной коники

Определения и двойное поколение

Примеры

Примечания

Рекомендации