WikiDer > Поверхностная диффузия

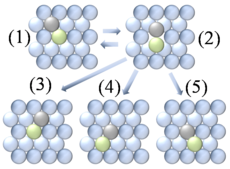
Поверхностная диффузия это общий процесс, включающий движение адатомы, молекулы, и атомные кластеры (частицы) при твердом материале поверхности.[1] В общем, этот процесс можно представить как прыжки частиц между соседними адсорбция сайтов на поверхности, как на рисунке 1. Так же, как навалом распространение, это движение обычно является термическим процессом, скорость которого возрастает с увеличением температуры. Многие системы демонстрируют диффузионное поведение, которое отличается от традиционной модели прыжков ближайшего соседа.[2] Туннельная диффузия - особенно интересный пример нетрадиционного механизма, в котором водород, как было показано, диффундирует на чистом металл поверхностей через квантовое туннелирование эффект.
Различные аналитические инструменты могут использоваться для разъяснять механизмы и скорости поверхностной диффузии, наиболее важными из которых являются полевая ионная микроскопия и сканирующая туннельная микроскопия.[3] Хотя в принципе процесс может происходить на самых разных материалах, большинство экспериментов проводится на кристаллических металлических поверхностях. Из-за экспериментальных ограничений большинство исследований поверхностной диффузии ограничено температура плавления из субстрат, и еще предстоит многое узнать о том, как эти процессы протекают при более высоких температурах.[4]
Скорость и механизмы поверхностной диффузии зависят от множества факторов, включая прочность поверхностной адчастицы. связь, ориентация поверхностной решетки, притяжение и отталкивание между поверхностными частицами и химический потенциал градиенты. Это важное понятие на поверхности фазообразование, эпитаксиальный рост, неоднородный катализ, и другие темы в наука о поверхности.[5] Таким образом, принципы поверхностной диффузии имеют решающее значение для химическое производство и полупроводник отрасли. Реальные приложения, в значительной степени зависящие от этих явлений, включают: каталитические преобразователи, интегральные схемы используется в электронных устройствах, и галогенид серебра соли, используемые в фотопленка.[5]
Кинетика
Кинетику поверхностной диффузии можно представить в терминах адатомов, находящихся на адсорбция сайты на 2D решетка, перемещаясь между соседними (ближайшими) участками адсорбции путем скачкообразного процесса.[1][6] Скорость прыжка характеризуется попыткой частота и термодинамический Фактор, определяющий вероятность того, что попытка приведет к успешному прыжку. Частота попыток ν обычно принимается просто как частота колебаний адатома, а термодинамический фактор - Фактор Больцмана зависит от температуры и Eразница, то потенциальная энергия барьер для распространения. Уравнение 1 описывает взаимосвязь:
Где ν и Eразница как описано выше, Γ - скорость скачка или скачка, T - температура, и kB это Постоянная Больцмана. Eразница должна быть меньше, чем энергия десорбции, чтобы происходила диффузия, иначе процессы десорбции будут доминировать. Важно отметить, что уравнение 1 показывает, насколько сильно скорость скачка зависит от температуры. Способ, которым происходит диффузия, зависит от соотношения между Eразница и kBТ как указано в термодинамическом факторе: когда Eразница
Случайная прогулка статистика описывает среднеквадратичное смещение диффундирующих видов по количеству прыжков N и расстояние за прыжок а. Количество успешных прыжков просто Γ умноженное на время, отведенное для диффузии, т. В самой базовой модели рассматриваются только прыжки ближайшего соседа и а соответствует расстоянию между ближайшими соседями адсорбционных центров. Среднеквадратичное смещение имеет вид:
Коэффициент диффузии определяется как:
куда для одномерной диффузии, как и в случае диффузии в канале, для двумерной диффузии и для трехмерного распространения.[8]
Режимы

Существует четыре различных общих схемы, по которым может иметь место диффузия.[9] Диффузия индикаторов и химическая диффузия различаются по степени покрытия адсорбатом на поверхности, в то время как собственная диффузия и диффузия с переносом массы различаются по природе диффузионной среды. И диффузия индикаторов, и собственная диффузия относятся к системам, в которых адчастицы находятся в относительно однородной среде, тогда как при химической диффузии и диффузии масс адчастицы сильнее зависят от окружающей среды.
- Распространение трассера описывает движение отдельных частиц по поверхности при относительно низких уровнях покрытия. На этих низких уровнях (<0,01 монослой) взаимодействие частиц невелико, и можно считать, что каждая частица движется независимо от других. Отдельный атом, диффундирующий на рисунке 1, является хорошим примером диффузии трассера.
- Химическая диффузия описывает процесс на более высоком уровне охвата, когда становятся важными эффекты притяжения или отталкивания между адатомами. Эти взаимодействия служат для изменения подвижности адатомов. В грубом виде рисунок 3 служит для демонстрации того, как адатомы могут взаимодействовать на более высоких уровнях покрытия. У адатомов нет «выбора», кроме как сначала двигаться вправо, а соседние адатомы могут блокировать участки адсорбции друг от друга.
- Внутренняя диффузия происходит на однородной поверхности (например, отсутствует шаги или же свободные места), например, одиночная терраса, на которой отсутствуют ловушки или источники адатомов. Этот режим часто изучается с помощью полевая ионная микроскопия, где терраса представляет собой острый наконечник образца, по которому диффундирует адчастица. Даже в случае чистой террасы на процесс может повлиять неоднородность по краям террасы.
- Распространение массопереноса имеет место в случае наличия источников и ловушек адчастиц, таких как перегибы, ступеньки и вакансии. Вместо того, чтобы зависеть только от скачкообразного потенциального барьера Eразница, диффузия в этом режиме теперь также зависит от энергии образования подвижных адчастиц. Таким образом, точная природа диффузионной среды играет роль в определении скорости диффузии, поскольку энергия образования адчастицы различна для каждого типа поверхностного элемента, как описано в Модель Terrace Ledge Kink.
Анизотропия
Ориентационная анизотропия проявляется в различиях как в скоростях, так и в механизмах диффузии при различных ориентация поверхности данного материала. Для данного кристаллического материала каждый Индекс Миллера самолет может отображать уникальные явления диффузии. Плотно упакованный поверхности, такие как fcc (111) имеют тенденцию иметь более высокие скорости диффузии, чем соответственно более «открытые» грани того же материала, такого как ГЦК (100).[10][11]
Направленная анизотропия относится к различию в механизме или скорости диффузии в определенном направлении на данной кристаллографической плоскости. Эти различия могут быть результатом либо анизотропии поверхностной решетки (например, прямоугольная решетка) или наличие ступенек на поверхности. Одним из наиболее ярких примеров направленной анизотропии является диффузия адатомов на каналированных поверхностях, таких как ГЦК (110), где диффузия по каналу намного быстрее, чем диффузия по каналу.
Механизмы
Адатом диффузия
Диффузия адатомов может происходить по разным причинам. Способ их диффузии важен, поскольку он может определять кинетику движения, температурную зависимость и общую подвижность поверхностных частиц, среди других параметров. Ниже приводится краткое изложение наиболее важных из этих процессов:[12]
- Прыжки или же прыжки концептуально является самым основным механизмом диффузии адатомов. В этой модели адатомы располагаются на сайтах адсорбции на поверхностной решетке. Движение происходит за счет последовательных прыжков на соседние узлы, количество которых зависит от характера решетки поверхности. На рисунках 1 и 3 показаны адатомы, диффундирующие посредством прыжкового процесса. Исследования показали наличие метастабильный переходные состояния между центрами адсорбции, в которых адатомы могут временно находиться.[13]
- Атомный обмен включает обмен между адатомом и соседним атомом в поверхностной решетке. Как показано на рисунке 4, после атомного обмена адатом занял место поверхностного атома, а поверхностный атом был перемещен и теперь стал адатомом. Этот процесс может происходить как при гетеродиффузии (например, Pt адатомы на Ni) и самодиффузии (например, адатомы Pt на Pt). С теоретической точки зрения до сих пор неясно, почему в одних системах механизм атомного обмена преобладает больше, чем в других. Текущая теория указывает на множество возможностей, включая растягивающие поверхностные напряжения, поверхностную релаксацию вокруг адатома и повышенную стабильность промежуточного продукта из-за того, что оба участвующих атома поддерживают высокие уровни координация на протяжении всего процесса.[14][15]
- Туннельная диффузия является физическим проявлением квантового туннельного эффекта, связанного с туннелированием частиц через диффузионные барьеры. Это может произойти в случае низкой диффузии частиц. масса и низкий Eразница, и наблюдалось в случае водород распространение на вольфрам и медь поверхности.[16] Это явление уникально тем, что в режиме преобладания туннельного механизма скорость диффузии практически не зависит от температуры.[17]
- Распространение вакансий может являться преобладающим методом поверхностной диффузии при высоких уровнях покрытия, приближающихся к полному. Этот процесс похож на то, как части скользят в "раздвижная головоломка". Непосредственно наблюдать диффузию вакансий очень сложно из-за обычно высоких скоростей диффузии и низкого уровня вакансий. концентрация.[18] На рисунке 5 показана основная тема этого механизма, хотя и в упрощенной форме.
Недавние теоретические работы, а также экспериментальные работы, выполненные с конца 1970-х годов, выявили замечательное разнообразие явлений поверхностной диффузии как в отношении кинетики, так и механизмов. Ниже приводится краткое изложение некоторых наиболее примечательных явлений:
- Прыжки в длину состоят из смещения адатома к месту адсорбции, не являющемуся ближайшим соседом. Они могут включать двойные, тройные и более длинные прыжки в том же направлении, что и прыжок ближайшего соседа, или они могут быть в совершенно разных направлениях, как показано на рисунке 6. Они были предсказаны теория существуют во многих различных системах и, как было показано экспериментально, имеют место при температурах всего 0,1 Тм (температура плавления). В некоторых случаях данные указывают на преобладание длинных скачков над процессом диффузии над одиночными скачками при повышенных температурах; явление переменной длины скачка выражается в различных характерных распределениях атомного смещения во времени (см. рисунок 7).[19]
- Прыжки с отскоком как эксперимент, так и моделирование показали, что имеют место в определенных системах. Поскольку движение не приводит к чистому смещению задействованного адатома, экспериментальные доказательства скачков отскока снова прибывают из статистической интерпретации атомных распределений. Скачок отскока показан на рисунке 6. Цифра немного обманчива, однако, поскольку скачки отскока имели место только экспериментально в случае одномерной диффузии на каналированной поверхности (в частности, скрытая копия (211) грань вольфрама).[20]
- Межканальная диффузия может возникнуть в случае поверхностей с канавками. Обычно преобладает внутриканальная диффузия из-за более низкого энергетического барьера для диффузии этого процесса. Было показано, что в некоторых случаях происходит перекрестный канал, который происходит аналогично тому, как показано на рисунке 8. Промежуточное положение «гантели» может привести к множеству конечных смещений адатомов и поверхностных атомов.[21]
- Атомный обмен на большие расстояния представляет собой процесс, в котором адатом внедряется в поверхность, как и в обычном механизме атомного обмена, но вместо атома ближайшего соседа возникает атом, находящийся на некотором расстоянии от исходного адатома. Как показано на рисунке 9, этот процесс наблюдался только при моделировании молекулярной динамики и еще не подтвержден экспериментально. Несмотря на этот обмен атомами на большие расстояния, а также множество других экзотических механизмов диффузии, ожидается, что они будут вносить существенный вклад при температурах, в настоящее время слишком высоких для прямого наблюдения.[22]
Кластерная диффузия
Кластерная диффузия включает движение атомных кластеров размером от димеры на островки, содержащие сотни атомов. Движение кластера может происходить за счет смещения отдельных атомов, участков кластера или всего кластера одновременно.[23] Все эти процессы включают изменение в кластере центр массы.
- Индивидуальные механизмы это те, которые включают движение одного атома за раз.[24]
- Краевая диффузия включает перемещение адатомов или вакансий на краях или изломах. Как показано на рисунке 10, мобильный атом сохраняет свою близость к кластеру на протяжении всего процесса.
- Испарение-конденсация включает атомы "испаряющийся»Из кластера на террасу в сопровождении«конденсация”Террасных адатомов на кластер, что приводит к изменению центра масс кластера. Хотя фигура 10, кажется, указывает на то, что один и тот же атом испаряется из кластера и конденсируется на нем, на самом деле это может быть другой атом, конденсирующийся из 2D-газа.
- Распространение чехарда похожа на краевую диффузию, но при этом диффундирующий атом фактически перемещается на вершину кластера, прежде чем обосноваться в другом месте от своего начального положения.
- Последовательное перемещение относится к процессу, включающему движение одного атома за раз, переходя к свободным ближайшим соседям.
 | 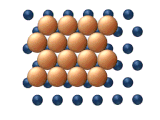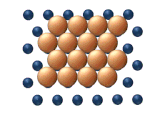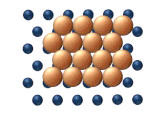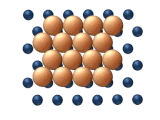 |
| а) вывих | (б) скольжение |
 |  |
| (c) Рептация | (d) Сдвиг |
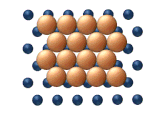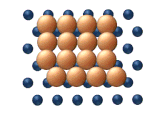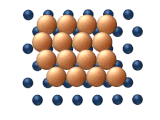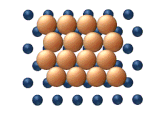
| Рис. 11. Согласованные механизмы диффузии кластеров. | |
- Согласованные механизмы это те, которые включают перемещение либо частей кластера, либо всего кластера одновременно.[25]
- Распространение дислокаций происходит, когда соседние субблоки кластера перемещаются строка за строкой посредством смещения вывих. Как показано на рисунке 11 (а), процесс начинается с зарождение дислокации, за которой следует то, что по сути является последовательным перемещением на согласованный основание.
- Скользящая диффузия относится к согласованному движению всего кластера одновременно (см. рисунок 11 (b)).
- Рептация является змееподобным движением (отсюда и название), включающим последовательное движение субблоков кластера (см. рисунок 11 (c)).
- Стрижка представляет собой согласованное смещение субъединицы атомов в кластере (см. рисунок 11 (d)).
- Зависимость от размера: скорость диффузии кластера сильно зависит от размера кластера, при этом больший размер кластера обычно соответствует более медленной диффузии. Однако это не универсальная тенденция, и в некоторых системах было показано, что скорость диффузии принимает периодическую тенденцию, при которой некоторые более крупные кластеры диффундируют быстрее, чем те, которые меньше их.[26]
Поверхностная диффузия и гетерогенный катализ
Поверхностная диффузия является критически важной концепцией в гетерогенном катализе, поскольку скорость реакции часто диктуется способностью реагентов «находить» друг друга на поверхности катализатора. При повышении температуры адсорбированные молекулы, молекулярные фрагменты, атомы и кластеры имеют тенденцию иметь гораздо большую подвижность (см. Уравнение 1). Однако с повышением температуры время адсорбции уменьшается, так как коэффициент kBT становится достаточно большим, чтобы адсорбированные частицы преодолели барьер для десорбции Q (см. Рисунок 2). Реакция термодинамика кроме того, из-за взаимодействия между повышенной скоростью диффузии и уменьшением времени адсорбции, повышенная температура может в некоторых случаях снизить общую скорость реакции.
Экспериментальный
Поверхностную диффузию можно изучать различными методами, включая как прямые, так и косвенные наблюдения. Два экспериментальных метода, которые оказались очень полезными в этой области исследований, - это полевая ионная микроскопия и сканирующая туннельная микроскопия.[3] Визуализируя смещение атомов или кластеров во времени, можно извлечь полезную информацию о том, как распространяются соответствующие виды - как механистическая, так и связанная со скоростью информация. К сожалению, для изучения поверхностной диффузии в атомистическом масштабе необходимо проводить исследования на строго чистых поверхностях и в сверхвысокий вакуум (UHV) условиях или в присутствии небольших количеств инертный газа, как в случае использования He или Ne в качестве газа изображения в полевая ионная микроскопия эксперименты.
Смотрите также
Рекомендации
- ^ а б Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 325
- ^ Антчак, Эрлих 2007, стр.39
- ^ а б Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 349
- ^ Антчак, Эрлих 2007, стр. 50, 59
- ^ а б Шусторович 1991, с. 109
- ^ Шусторович 1991, с. 109-111
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 327
- ^ Структура и динамика поверхностей II (Topics in Current Physics), W. Schommers, P. Von Blanckenhagen, ISBN 0387173382. Глава 3.2, с. 75
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 330-333
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 333
- ^ Шусторович 1991, с. 114-115
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 336-340
- ^ Шусторович 1991, с. 111
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 338
- ^ Антчак, Эрлих 2007, стр. 48
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 338-340
- ^ Шусторович 1991, с. 115
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 340-341
- ^ Антчак, Эрлих 2007, стр. 51
- ^ Антчак, Эрлих 2007, стр. 58
- ^ Антчак, Эрлих 2007, стр. 40–45
- ^ Антчак, Эрлих 2007, стр. 48-50
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 341
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 343-344
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 343-345
- ^ Оура, Лифшиц, Саранин, Зотов, Катаяма, 2003, с. 341-343
Цитированные работы
- Г. Антчак, Г. Эрлих. Отчеты по науке о поверхности 62 (2007), 39-61. (Рассмотрение)
- Оура, К .; В.Г. Лифшиц; А.А. Саранин; СРЕДНИЙ. Зотов; М. Катаяма (2003). Наука о поверхности: введение. Springer-Verlag Berlin Heidelberg. ISBN 3-540-00545-5.
- Шусторович, Е. (1991). Энергетика реакций на поверхности металла: теория и приложения к гетерогенному катализу, хемосорбции и поверхностной диффузии. VCH Publishers, Inc. ISBN 3-527-27938-5.