WikiDer > Колонка Тейлора
А Колонка Тейлора это явление динамики жидкости, которое возникает в результате Эффект Кориолиса. Он был назван в честь Джеффри Ингрэм Тейлор. Вращающиеся жидкости, которые возмущаются твердым телом, имеют тенденцию образовывать столбцы, параллельные оси вращения, называемые столбцами Тейлора.
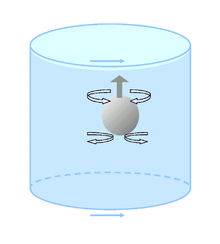
Объект, движущийся параллельно оси вращения во вращающейся жидкости, испытывает большую силу сопротивления, чем та, которую он испытывал бы в невращающейся жидкости. Например, сильно плавучий мяч (такой как мяч для пинг-понга) будет подниматься на поверхность медленнее, чем в невращающейся жидкости. Это связано с тем, что жидкость на пути мяча, который выталкивается с пути, имеет тенденцию циркулировать обратно к точке, от которой она отодвинута, из-за эффекта Кориолиса. Чем выше скорость вращения, тем меньше радиус инерционного круга, по которому движется жидкость.
В невращающейся жидкости жидкость разделяется над поднимающимся шаром и закрывается под ним, оказывая относительно небольшое сопротивление шару. Во вращающейся жидкости шар должен подтолкнуть вверх целый столб жидкости над собой, и ему необходимо тащить за собой целый столб жидкости, чтобы подняться на поверхность.
Таким образом, вращающаяся жидкость демонстрирует некоторую жесткость.
История
Колонны Тейлора впервые наблюдали Уильям Томсон, лорд Кельвин, в 1868 г.[1][2] Колонны Тейлора были представлены в демонстрациях лекций Кельвина в 1881 году.[3] и Джоном Перри в 1890 году.[4] Явление объясняется через Теорема Тейлора – Праудмена, и это было исследовано Тейлором,[5] Грейс,[6] Стюартсон,[7] и Максворти[8]- среди других.
Теория
Колонки Тейлора были тщательно изучены. Для Re<<1, Ek<<1, Ro<< 1, уравнение сопротивления цилиндра радиуса, а, было найдено следующее соотношение.[7][9]
Чтобы вывести это, Мур и Саффман решили линеаризованную Уравнение Навье – Стокса вдоль в цилиндрических координатах,[9] где некоторые из вертикальных и радиальных компонентов вязкого члена считаются малыми по сравнению с членом Кориолиса:
Чтобы решить эти уравнения, мы также включаем условие сохранения объема:
Мы используем соотношение совместимости Экмана для этой геометрии, чтобы ограничить форму скорости на поверхности диска:
Полученные поля скоростей могут быть решены в терминах Функции Бесселя.
посредством чего для Ek<< 1 функция А (к) дан кем-то,
Интегрируя уравнение для v, мы можем найти давление и, следовательно, силу сопротивления, заданную первым уравнением.
использованная литература
- ^ Джеймс Томсон (брат лорда Кельвина) (1868 г.) Письмо Уильяму Томсону (30 сентября). Библиотека Университета Глазго, MS Kelvin T120.
- ^ Веласко Фуэнтес, О. У. (2008). «Открытие Кельвином колонн Тейлора» (PDF). Европейский журнал механики. Б / Жидкости. 28 (3): 469–472. Дои:10.1016 / j.euromechflu.2008.11.002. Архивировано из оригинал (PDF) 23 июля 2011 г.
- ^ Томсон, У. (1882) «Упругость рассматривается как возможный способ движения». Труды Королевского института, т. 9, страницы 520–521; Также в: Популярные лекции и адреса, т. 1, страницы 142–146. См. Также: Томсон В. (1887 г.) «Об устойчивости стационарного и периодического движения жидкости». Философский журнал, т. 23, страницы 459–464. Также в: Математические и физические статьи (Кембридж, Англия: Cambridge University Press, 1910), т. 4. С. 166-172.
- ^ Перри, Дж. Волчки. «Лекция оперативников» на собрании Британской ассоциации в Лидсе 6 сентября 1890 года. (Лондон: Общество распространения христианских знаний, 1910 г.).
- ^ Тейлор, Г. (1922) «Движение шара во вращающейся жидкости». Труды Лондонского королевского общества A, т. 102, страницы 180–189.
- ^ Грейс, С.Ф. (1922) «Свободное движение шара во вращающейся жидкости параллельно оси вращения». Труды Лондонского королевского общества A, т. 102, страницы 89–111.
- ^ а б Стюартсон, К. (1952) "О медленном движении шара вдоль оси вращающейся жидкости". Труды Кембриджского философского общества, т. 48, страницы 168–177.
- ^ Максворти, Т. (1968) «Наблюдаемое движение сферы через короткий вращающийся цилиндр жидкости». Журнал гидромеханики, т. 31, страницы 643–655. См. Также: Максворти Т. (1970) «Поток, создаваемый сферой, движущейся вдоль оси вращающейся слегка вязкой жидкости». Журнал гидромеханики, т. 40, страницы 453–479.
- ^ а б Мур, Д. У .; Саффман, П. Г. (18 сентября 1969 г.). «Структура слоев свободного вертикального сдвига во вращающейся жидкости и движение, создаваемое медленно поднимающимся телом». Философские труды Лондонского королевского общества A: математические, физические и инженерные науки. 264 (1156): 597–634. Bibcode:1969РСПТА.264..597М. Дои:10.1098 / Рста.1969.0036. ISSN 1364-503X.
дальнейшее чтение
- Бреннер, Майкл П .; Стоун, Ховард А. (май 2000 г.). "Современная классическая физика через работы Г. И. Тейлора". Физика сегодня. 53 (5): 30–35. Bibcode:2000ФТ .... 53э..30Б. Дои:10.1063/1.883100.
внешние ссылки
- Колонны Тейлора (Марта Бакли, Массачусетский технологический институт)
- Динамика жидкости проигрывателя: эксперимент с колонной Тейлора (Лаборатория спиновых движений UCLA)