WikiDer > Тетрагональные дифеноидные соты

Тетрагональные дифеноидные тетраэдрические соты
Тип	выпуклые однородные соты двойной
Диаграмма Кокстера-Дынкина
Тип ячейки	Тетрагональный дисфеноид
Типы лица	равнобедренный треугольник {3}
Фигура вершины	тетракис шестигранник
Космическая группа	Я3м (229)
Симметрия	[[4,3,4]]
Группа Кокстера	${displaystyle {ilde {C}} _ ​​{3}}$, [4,3,4]
Двойной	Усеченные кубические соты
Характеристики	клеточно-транзитивный, лицо переходный, вершинно-транзитивный

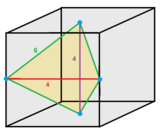
В тетрагональный дисфеноид тетраэдрические соты заполняет пространство мозаика (или же соты) в Евклидово 3-пространство состоящий из идентичных тетрагональный дисфеноидальный клетки. Ячейки лицо переходный с 4 идентичными равнобедренный треугольник лица. Джон Хортон Конвей называет это сплюснутый тетраэдрил или сокращено до обтетрагедрилла.^[1]

Ячейку можно рассматривать как 1/12 трансляционного куба с центрами вершин на двух гранях и двух ребрах. Четыре его ребра принадлежат 6 ячейкам, а два ребра - 4 ячейкам.

Тетраэдрические дисфеноидные соты двойственны однородной усеченные кубические соты.

Его вершины образуют A^*
₃ / D^*
₃ решетка, которая также известна как Телоцентрированный кубик решетка.

Геометрия

Эти соты вершина фигуры это куб тетракиса: 24 дифеноида встречаются в каждой вершине. Объединение этих 24 дифеноидов образует ромбический додекаэдр. Каждый край мозаики окружен четырьмя или шестью дифеноидами, в зависимости от того, образует ли он основание или одну из сторон смежных граней равнобедренного треугольника соответственно. Когда край образует основание соседних с ним равнобедренных треугольников и окружен четырьмя дифеноидами, они образуют неправильную форму. октаэдр. Когда ребро образует одну из двух равных сторон смежных граней равнобедренного треугольника, шесть дифеноидов, окружающих край, образуют особый тип параллелепипед называется треугольный трапецоэдр.

Ориентацию тетрагональной дифеноидной соты можно получить, начав с кубические соты, разделив его на плоскости ${displaystyle x = y}$, ${displaystyle x = z}$, и ${displaystyle y = z}$ (т.е. деление каждого куба на пути-тетраэдры), затем сдавливая его по главной диагонали, пока расстояние между точками (0, 0, 0) и (1, 1, 1) не станет таким же, как расстояние между точками (0, 0, 0) и (0, 0, 1).

Кубические соты Hexakis

Кубические соты Hexakis Пирамидиль[2]
Тип	Двойные однородные соты
Диаграммы Кокстера – Дынкина
Клетка	Равнобедренный квадратная пирамида
Лица	Треугольник квадрат
Космическая группа Обозначение фибрифолда	Вечера3м (221) 4−:2
Группа Кокстера	${displaystyle {ilde {C}} _ ​​{3}}$, [4,3,4]
фигуры вершин	,
Двойной	Усеченные кубические соты
Характеристики	Клеточно-транзитивный

В кубические соты hexakis равномерное заполнение пространства мозаика (или же соты) в трехмерном евклидовом пространстве. Джон Хортон Конвей называет это пирамидилла.^[3]

Ячейки можно увидеть в трансляционном кубе, используя 4 вершины на одной грани и центр куба. Края окрашены в зависимости от количества ячеек вокруг каждой из них.

Это можно рассматривать как кубические соты где каждый куб разделен центральной точкой на 6 квадратная пирамида клетки.

Есть два типа плоскостей граней: один как квадратная черепица, и сплющенный треугольная черепица с удалением половины треугольников как дыры.

Плитка самолет
Симметрия	p4m, [4,4] (* 442)	pmm, [∞, 2, ∞] (* 2222)

Связанные соты

Он двойственен усеченные кубические соты с октаэдрическими и усеченными кубическими ячейками:

Если квадратные пирамиды пирамидилла находятся присоединился на их основании создается еще одна сота с идентичными вершинами и ребрами, называемая квадратные бипирамидальные соты, или двойник ректификованные кубические соты.

Это аналог двумерного квадратная плитка тетракис:

Квадратные бипирамидальные соты

Квадратные бипирамидальные соты Сплюснутый октаэдр[4]
Тип	Двойные однородные соты
Диаграммы Кокстера – Дынкина
Клетка	Квадратная бипирамида
Лица	Треугольники
Космическая группа Обозначение фибрифолда	Вечера3м (221) 4−:2
Группа Кокстера	${displaystyle {ilde {C}} _ ​​{3}}$, [4,3,4]
фигуры вершин	,
Двойной	Ректифицированные соты кубической формы
Характеристики	Клеточно-транзитивный, Лицо-переходный

В квадратные бипирамидальные соты равномерное заполнение пространства мозаика (или же соты) в трехмерном евклидовом пространстве. Джон Хортон Конвей называет это сплюснутый октаэдр или сокращено до обоктаэдр.^[5]

Можно увидеть ячейку, расположенную внутри трансляционного куба с 4 вершинами по середине и 2 вершинами на противоположных гранях. Края окрашены и помечены количеством ячеек по краю.

Это можно рассматривать как кубические соты где каждый куб разделен центральной точкой на 6 квадратная пирамида клетки. Исходные кубические сотовые стенки удаляются, и пары квадратных пирамид объединяются в квадратные бипирамиды (октаэдры). Его вершинно-краевой каркас идентичен кубические соты hexakis.

Есть один вид плоскостей с гранями: плоские. треугольная черепица с половиной треугольников как дыры. Они разрезают исходные кубики по диагонали. Это также квадратная черепица плоскости, которые существуют как безликие дыры проходящие через центры октаэдрических ячеек.

Плитка самолет	Квадратная плитка "дыры"	сплющенный треугольная черепица
Симметрия	p4m, [4,4] (* 442)	pmm, [∞, 2, ∞] (* 2222)

Связанные соты

Он двойственен ректификованные кубические соты с октаэдрическими и кубооктаэдрическими ячейками:

Филлические дисфеноидальные соты

Эта секция может быть сбивает с толку или неясно читателям. В частности, чем это отличается от разделения куба всего на шесть тетраэдров и последующего преобразования? И чем оправдано описание этого в статье про разные соты ?. Пожалуйста, помоги нам прояснить раздел. Возможно обсуждение этого вопроса на страница обсуждения. (Май 2018) (Узнайте, как и когда удалить этот шаблон сообщения)

Филлические дисфеноидальные соты Восьмая пирамидилла[6]
(Нет изображения)
Тип	Двойные однородные соты
Диаграммы Кокстера-Дынкина
Клетка	Филлический дисфеноид
Лица	Ромб Треугольник
Космическая группа Обозначение фибрифолда Обозначение Кокстера	Я3м (229) 8о:2 [[4,3,4]]
Группа Кокстера	[4,3,4], ${displaystyle {ilde {C}} _ ​​{3}}$
фигуры вершин	,
Двойной	Усеченные кубические соты
Характеристики	Клеточно-транзитивный, лицо переходный

В филлические дисфеноидальные соты равномерное заполнение пространства мозаика (или же соты) в трехмерном евклидовом пространстве. Джон Хортон Конвей называет это Восьмая пирамидилла.^[7]

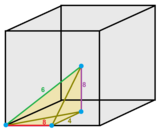
Ячейку можно рассматривать как 1/48 трансляционного куба с расположенными вершинами: один угол, один центр края, центр одной грани и центр куба. Цвета краев и метки указывают, сколько ячеек существует по краю.

Связанные соты

Он двойственен усеченные кубические соты:

Смотрите также

• Архитектурная и катоптическая мозаика
• Кубические соты
• космический каркас
• Усеченные четырехгранные соты Triakis

Рекомендации

• Гибб, Уильям (1990), «Выкройки из бумаги: сплошные формы из метрической бумаги», Математика в школе, 19 (3): 2–4, перепечатано в Причард, Крис, изд. (2003), Меняющаяся форма геометрии: празднование века геометрии и преподавания геометрии, Cambridge University Press, стр. 363–366, ISBN 0-521-53162-4.
• Сенешаль, Марджори (1981), «Какие тетраэдры заполняют пространство?», Математический журнал, Математическая ассоциация Америки, 54 (5): 227–243, Дои:10.2307/2689983, JSTOR 2689983.
• Конвей, Джон Х.; Берджел, Хайди; Гудман-Штраус, Хаим (2008). «21. Именование архимедовых и каталонских многогранников и мозаик». Симметрии вещей. А. К. Петерс, Лтд., Стр. 292–298. ISBN 978-1-56881-220-5.